Ввод энергоблоков АЭС - Экспертная оценка надежности оборудования и персонала в условиях нечеткой информации по отказам

Методы оценки показателей надежности при вводе в эксплуатацию.

В предыдущем параграфе приведен анализ отказов и дефектов оборудования при вводе в эксплуатацию и их влияние на фактическую продолжительность этапов ввода в эксплуатацию. Показано, что на практике имеющаяся информация по отказам зачастую носит нечеткий характер.
Далее, рассматривая отказы и надежность оборудования, будем иметь в виду, что аналогично можно оценивать отказы и риски антропогенного происхождения (ошибки персонала, недостатки проекта и т.п.)
Если информация по отказам оборудования носит четкий характер (т.е. корректно приведены время отказа системы, причина и описание отказа с четким обозначением отказавшего элемента), особых препятствий и затруднений при оценках показателей надежности исследуемого оборудования и их влияния на сроки ввода в эксплуатацию не возникает. Существует множество различных методик, позволяющих делать такие оценки [121, 122].
Однако основные трудности возникают тогда, когда информация по отказам оборудования оказывается неопределенной.  Примером такой информации могут служить некоторые данные по отказам оборудования с пропусками в графе «время отказа», «размытое» или нечеткое описание причины отказа, не позволяющее определить первопричину отказа той или иной системы. Довольно часто в графе «описание и причина отказа» можно обнаружить некорректно введённую информацию, при использовании которой не представляется возможным получить какие-либо количественные характеристики для описания надёжности рассматриваемого объекта. Зачастую в графе «причина отказа» можно обнаружить фразу «причина отказа не установлена» или «вина проектной организации» и т.п. Этот факт значительно затрудняет использование информации по отказам при анализе данных и подготовке информационно-аналитических материалов об опыте ввода в эксплуатацию энергоблоков АС, а также при подготовке исходных данных для расчета показателей надежности систем и оборудования и оценки влияния этих показателей на сроки выполнения работ по вводу в эксплуатацию.
Тем не менее, обоснованное использование любой, даже нечеткой информации об отказах является полезной, так как повышает точность оценок показателей надежности. Поэтому в настоящее время является актуальной проблема разработки методов учёта нечёткой информации при оценках показателей надёжности оборудования, в том числе для планирования пусконаладочных работ.
Оценки характеристик надёжности, как правило, основываются на подходе, базирующемся на теории вероятностей [121]. Этот подход в большинстве случаев зависит от моделей, использующих логические структуры: дерево событий, дерево отказов. Для получения возможного разброса оценок характеристик надёжности необходим корректный учет неопределенностей входных параметров. Эти неопределенности могут быть обусловлены ошибками измерений, интерполяции или экстраполяции, дискретизации и аппроксимации, различными допущениями, вариабельностью и т.п. По современным представлениям неопределенности входных параметров, характеризующих исходные события аварийных ситуаций, можно условно отнести к одному из двух классов: случайному (вероятностному) и нечеткому. Соответственно и модели, в рамках которых осуществляются оценки риска, можно называть вероятностными и нечеткими. Вероятностная модель планирования ввода в эксплуатацию и методика оценки основанных на ней критериев надежности и эффективности ввода в эксплуатацию рассмотрены в гл. 13.
Оценка надёжности оборудования энергоблоков АС, информация об эксплуатации (вводе в эксплуатацию) которых относится к классу нечётких, большей частью опирается на оценку экспертов. Экспертные оценки служат эффективным, а иногда и единственным средством решения большого числа неформальных задач в различных областях человеческой деятельности. Обычно они используются там, где некоторый объект характеризуется только качественными свойствами, которые непригодны для обработки. Для получения количественной информации об объекте обращаются к методу экспертных оценок. Экспертные методы используют эвристические возможности человека, позволяя на основе знаний, опыта и интуиции специалистов, работающих в данной области, получить оценку исследуемых явлений. Обоснованию и математическим основам экспертных методов посвящено значительное число работ [123, 124]. При использовании мнений группы экспертов предполагается, что организованное взаимодействие между специалистами позволит компенсировать смещение оценок отдельных членов группы и сумма информации, имеющейся в распоряжении группы экспертов, будет больше, чем информация любого члена группы. В общем случае предполагается, что мнение группы экспертов надежнее, чем мнение отдельного индивидуума, т.е. две группы одинаково компетентных экспертов с большей вероятностью дадут аналогичные ответы на ряд вопросов, чем два индивидуума.
Далее приведен метод, позволяющий структурировать нечеткую информацию по отказам, а также количественно оценить нечеткую информацию по отказам оборудования, обеспечивая данные для дальнейших расчетов [125].
В основе предложенного метода оценки характеристик надежности лежит экспертный опрос с применением лингвистических переменных теории нечетких множеств. Использование экспертного опроса и лингвистических переменных в задачах оценки характеристик надежности дает возможность определения и оценки соответствующих факторов риска (рисков), приводящих к увеличению продолжительности и стоимости работ на этапах сооружения и ввода в эксплуатацию и влияющих на сроки ввода энергоблока в эксплуатацию.
На рис. 11.4 приведена схема обработки любой информации об отказах и причинах отказов оборудования при ПНР на энергоблоке АС.

Рис. 11.4. Схема процесса подготовки данных по отказам оборудования энергоблока АС к проведению расчетов показателей их надежности в процессе ПНР

В соответствии с этой схемой, если информация об отказах «четкая», то она сразу подвергается количественной обработке методами, приведенными, например, в [121, 122]. В случае «нечеткой» информации ее обработка может идти двумя путями. Наиболее сложен случай (правая ветвь на схеме), когда нечеткой является как информация о причине отказа системы (например, о том, отказ какого именно элемента системы привел к ее отказу), так и информация о показателях надежности элементов системы. Случай, когда нечеткой является только информация о причине отказа системы, более прост и формально является частным случаем более сложной ситуации, описанной выше. Далее методика обработки нечеткой информации изложена на самом сложном примере (правая ветвь на схеме рис. 11.4).

Понятие нечеткого множества.

Математическая теория нечетких множеств, предложенная Л. Заде [126], позволяет описывать нечеткие понятия и знания, оперировать этими знаниями и делать нечеткие выводы. С выходом [127] началось развитие новой теории, предназначенной для изучения и анализа систем, в которых основная роль принадлежит суждениям и решениям человека. Поскольку эти системы связаны с принципиально нечетким (размытым, расплывчатым) характером информации, то сама новая теория получила название «теории нечетких множеств», являющейся обобщением обычной (четкой) теории множеств.
Исходным понятием обычной теории множеств является понятие принадлежности z - А элемента ζ некоторого множества Ζ к определенному подмножеству А - Ζ. Для выражения этой принадлежности можно использовать и другое понятие — характеристическую функцию χΛ(Ζ), значение которой указывает, является ли ζ элементом А:

(11.1)

 Однако этого понятия оказалось недостаточно для рассмотрения ситуаций, которые описываются с помощью нечетко определенных понятий типа «множество высоких людей», «множество чисел много больше 10» и т.д. В основе теории нечетких множеств лежит представление о том, что составляющие множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно, принадлежать данному множеству с различной степенью. При таком подходе высказывание типа «элемент принадлежит множеству А» теряет смысл, поскольку необходимо указать, с какой степенью элемент принадлежит данному множеству. Это множество степеней принадлежности может оцениваться на бесконечной шкале действительных (или рациональных) чисел от 0 до 1, или на части чисел интервала [0,1], в том числе и на конечной шкале.
Для нечеткого подмножества, являющегося расширением понятия множества в классическом смысле, на пространстве объектов Ζ=(z) вводится уже не функционал вида (11.1), а характеристическая функция, задающая для всех элементов степень наличия у них некоторого свойства, по которому они относятся к подмножеству. Эта характеристическая функция для нечеткого множества традиционно носит название функции принадлежности.
Нечеткое подмножество А множества Ζ характеризуется функцией принадлежности μΑ:Ζ → [0,1], которая ставит в соответствие каждому элементу z е Ζ число μΑ(Ζ) из интервала [0,1], характеризующее степень принадлежности элемента z подмножеству А. Причем 0 и 1 представляют собой соответственно низшую и высшую степени принадлежности элемента к определенному подмножеству.
Одной из возможных и, пожалуй, наиболее интересных для применения особенностей аппарата нечетких множеств в области оценки надежности является его способность оперировать с качественными понятиями с помощью лингвистических переменных (лингвистических термов) [128]. Подобные переменные дают возможность использовать естественный язык для получения количественных результатов.
Лингвистические термы можно эффективно использовать, например, для описания события А и меры возможности его наступления P(t) в течение времени t при оценках риска, когда количественная информация отсутствует, и эксперты могут дать только качественные оценки.
Необходимость использования лингвистических переменных обоснована также тем, что при обработке данных по отказам часто возникает сложность в проведении расчетов, связанная с отсутствием точных данных (полное или частичное отсутствие, невозможность прочтения — расшифровки данных) по времени отказа рассматриваемой системы. В этом случае необходимо определиться не только с элементом, отказ которого стал причиной отказа всей системы, но и с наработкой на отказ этого элемента.
Таким образом, нечеткие модели характеристик надежности позволяют получать их количественные оценки в случае нечеткой, неопределенной, а также качественной информации (т.е. той информации, которая часто поступает с энергоблока АС).

Определение причины отказа системы.

Для определения причины отказа системы предлагается реализовать следующий метод экспертных оценок с максимальной функцией принадлежности этой причины к отказу всей системы. Процедура экспертного опроса делится на следующие этапы:
Первый этап. На первом этапе организаторы опроса выдвигают несколько предположений о том, что явилось, по их мнению, главной причиной нарушения нормальной эксплуатации рассматриваемой системы. Группе, состоящей из т экспертов предоставляется информация о возможной причине выхода из строя этой системы. Среди выдвигаемых предположений можно выделить три основные группы:

1. отказ оборудования;
2. ошибки человека;
3. внешнее (ие) воздействие (ия).

Выдвинутые предположения фиксируются в таблице опросного листа экспертов (табл. 11.3).
В таблице строки с номерами от 1 до п содержат точное указание события (отказ элемента системы, ошибка эксплуатационного персонала с указанием рабочего места, внешний фактор), повлекшего за собой отказ всей системы. Значения лингвистических переменных с номерами от 1 до п предоставляются организаторами экспертного опроса. Также отводится место для того, чтобы эксперты выдвигали свои предположения о причине возникновения рассматриваемого события, в строках с номерами от 1 до h — дополнительные предположения, выдвинутые экспертами.  

Таблица 11.3. Таблица опросного листа нескольких экспертов

При получении дополнительных предположений от экспертов проводится повторный опрос с включением в опросный лист новых данных, полученных от экспертов. Помимо самой таблицы, в заглавной части опросного листа приводится подробная (насколько это возможно) информация об отказе рассматриваемой системы. Информация по этому отказу полностью (без «вырезания», корректировки текста и комментариев со стороны организаторов опроса) переносится из соответствующей графы журнала учета технической неисправности оборудования.
Второй этап заключается в подборе группы экспертов. Экспертная группа составл 1ется на основании [129]. Участники экспертного опроса должны отвечать минимальному набору предъявляемых требований: высокому уровню общей эрудиции, высокому профессиональному уровню в оцениваемой области, способности перспективно мыслить и наличию производственного и исследовательского опыта в данной области [130].
Третий этап заключается в проведении самого опроса экспертов. В ходе опроса, каждый j-й эксперт выставляет оценку из интервала [0;1] в ί-й строке, выражая свою уверенность в том, что главной причиной выхода из строя рассматриваемой системы стала именно i-я. Выставляя оценку 0, эксперт выражает своё полное несогласие с тем, что данная причина могла вызвать возникновение отказа системы, и наоборот, выставляя оценку 1, эксперт выражает свою полную уверенность в том, что данная причина могла вызвать возникновение отказа рассматриваемой системы. Соответственно, выставляя некоторую промежуточную оценку (0,1; 0,2; 0,3; 0,4; ...), эксперт показывает степень уверенности при принятии решения по данному вопросу.
В этой связи возникает ряд проблем, связанных с формированием обобщенного метрического носителя для сопряжения лингвистической шкалы с числовой шкалой. Наиболее ярким примером обобщенного метрического носителя (обобщенного показателя), позволяющего связать лингвистическую и числовую шкалы, является функция желательности Харрингтона [128]. Стандартные отметки на шкале желательности приведены в табл. 11.4. Значение μ(χ) = 0,37 обычно соответствует границе допустимых значений.

Таблица 11.4. Шкала желательности

Одним из основных условий использования в ходе экспертного опроса разнородных лингвистических переменных является необходимость сопряжения лингвистической шкалы с числовой шкалой за счет упомянутого выше обобщенного метрического носителя. Для построения обобщенного метрического носителя необходимо знать шкалу лингвистических переменных, т.е. перечень всех её значений.
Для анализа информации по отказам оборудования АЭС предлагается использовать шкалу желательности (табл. 11.5), аналогичную приведенной в табл. 11.4, но с иначе сформулированными лингвистическими переменными, более подходящими для данной предметной области. Этой таблицей рекомендуется руководствоваться экспертам при проставлении в опросном листе оценок степени своей уверенности по решаемому вопросу.
Четвертый этап. На этом этапе проводится анализ результатов экспертного опроса т специалистов. На основе экспертной оценки строится функция принадлежности μ(χ) для каждой строки табл. 11.3, что в нашем случае показывает степень принадлежности события к отказу системы: (11.2) где т — число экспертов; i = 1,n+h — рассматриваемый элемент; kj — коэффициент компетентности j-го эксперта; хij — оценка j-го эксперта значения переменной с координатами (i,j) из опросного листа нескольких экспертов (табл. 11.3).

Информация, полученная от экспертов, должна быть тщательно проверена на согласованность мнений экспертов, ведь результаты работы группы экспертов неизбежно будут содержать отпечаток субъективизма, вносимого как самими экспертами, так и организаторами экспертного опроса.  Таблица 11.5. Шкала желательности

Это является неизбежной платой за возможность получить количественные оценки там, где раньше ограничивались лишь качественным описанием. Поэтому обработка результатов экспертного опроса включает оценку степени согласованности мнений экспертов и выявление причин неоднородности. Только при согласованности мнений экспертов можно утверждать, что в результате экспертизы получена достоверная информация.
Определение согласованности мнений экспертов производится вычислением числовой меры (коэффициента компетентности кj), характеризующей степень близости индивидуальных мнений (оценок). Анализ значений меры согласованности способствует выработке правильного суждения об общем уровне знаний по решаемой проблеме.
Для получения групповой оценки в этом случае можно воспользоваться средним значением оценки для каждого объекта (11.2).
Коэффициент компетентности является нормированной величиной:

Коэффициенты компетентности экспертов можно вычислить по апостериорным данным, т.е. по результатам оценки рассматриваемых событий, входящих в список причин отказа системы. Основной идеей этого вычисления является предположение о том, что компетентность эксперта должна оцениваться по степени согласованности его оценок с групповой оценкой объектов.
Алгоритм вычисления коэффициентов компетентности экспертов имеет вид рекуррентной процедуры [130]:

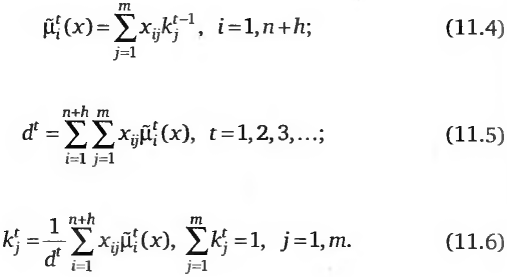
Вычисления начинаются c t=1. В (11.4) начальные значения коэффициентов компетентности принимаются одинаковыми и равными кj=1/т. Подробное описание определения коэффициентов компетентности экспертов приведено в [130]. Там же рассмотрен вопрос о сходимости рекуррентной процедуры вычисления коэффициентов компетентности экспертов.
Следует отметить, что чем больше различия в кj для разных экспертов, тем хуже согласованность их мнений и больше различие в уровне их знаний в данной проблеме. Например, в пределе, если для какого-либо р-го эксперта в результате оценок получено кр = 1, а для остальных — коэффициенты компетентности равны нулю, то такая группа экспертов не может считаться хорошо подобранной.
После определения коэффициентов компетентности экспертов, по формуле (11.2) находим функции принадлежности для каждого элемента, находящегося на рассмотрении.
Пятый этап. Все рассмотренные возможные причины отказа системы расставляются по приоритетам: первой возможной причиной считается имеющая самую большую функцию принадлежности. Так расставляются все причины по мере убывания функции принадлежности. Окончательное решение о причине отказа системы может быть только волевым.

Определение неизвестного показателя надежности элемента.

Предположим, в соответствии с процедурой экспертного опроса, описанного выше, установлено, что причиной отказа системы явился отказ какого-то ее элемента, а показателя его надежности (например, средней наработки на отказ) в справочниках нет. Предположим также, что длительность работы элемента в составе системы из описания ее отказа определить невозможно, и поэтому невозможно использовать какую-либо процедуру оценки показателей надежности из предложенных в [121, 122]. В этой ситуации также плодотворной может оказаться изложенная процедура экспертного опроса с последующей числовой обработкой ее результатов, использующей методы теории нечетких множеств для анализа лингвистических переменных.
Заметим, что в данном случае и таблица опросного листа нескольких экспертов (см. табл.11.3), и таблица со шкалой желательности (см. табл. 11.5) должны выглядеть несколько иначе.
Следует отметить, что значений лингвистических переменных и их комбинаций так много, что отобразить все возможные случаи в опросном листе не представляется возможным. Наиболее приемлемой, по мнению авторов, является процедура учета лингвистических переменных, представляющих собой высказывания типов «ограничение» и «цель» [131] с использованием числовых значений. Примерами высказываний типа «цель» могут служить следующие: «наработка на отказ компрессора должна быть 3-105 ч» или «расходомер был поставлен в работу 25.05.95». В свою очередь, высказывания типа «ограничение» могут быть двух видов: высказывания, определяющие нижнюю границу исследуемой величины (например, «наработка на отказ компрессора должна быть не меньше 3 · 105 ч» или «расходомер был поставлен в работу не позднее, чем 25.05.95»), и высказывания, определяющие верхнюю границу (например, «наработка на отказ компрессора должна быть не больше 3-105 ч» или «расходомер был поставлен в работу не ранее, чем 25.05.95»).
Таким образом, в ходе проведения опроса группы экспертов имеет смысл ограничиться использованием следующих лингвистических переменных: «...значение должно быть близко к ...», «предполагаемое значение исследуемой величины должно быть больше чем ...», «предполагаемое значение исследуемой величины должно быть не меньше чем ...» и т.п.

Таблица 11.6. Таблица опросного листа нескольких экспертов при оценке наработки на отказ системы

В результате организаторы опроса предъявляют группе из т экспертов набор, состоящий из лингвистических переменных А1,А2, ..., Af— определяющих нечеткую цель, Β1,В2, ..., Βd— определяющих нечеткое нижнее ограничение для исследуемой величины и Гъ Г2, —,rg — определяющих нечеткое верхнее ограничение. Соответственно, значения числовых переменных, допустим наработки на отказ элементов, взятых из соответствующих лингвистических переменных, будут: α1, α2, ..., αf— нечеткая цель, β1, β2, ..., βd — нечеткое нижнее ограничение, γ2, γ2, ..., yg — нечеткое верхнее ограничение. Следовательно, опросный лист экспертов должен иметь такой вид как показано в табл. 11.6,а, шкала желательности — в табл. 11.7
Производится анализ результатов экспертного опроса m специалистов. На основе экспертной оценки строятся функции принадлежности μi(αi), μi(βi), μi(γi) (в данном случае они показывают степень предпочтительности рассматриваемой лингвистической переменной, а точнее наработок на отказ αi, βi, γi, взятых из соответствующих лингвистических переменных):

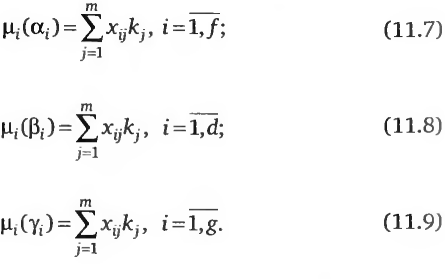
Таблица 11.7. Шкала желательности

где m — число экспертов; kj — коэффициент компетентности j-ro эксперта, определяется из рекуррентной процедуры (11.4)— (11.6); — оценка j-го эксперта значения переменной с координатами (i,j) из опросного листа (см. табл. 11.6).
Далее необходимо определить значение наработки на отказ: α — определяющее нечеткую цель; β — определяющее нечеткое нижнее ограничение; γ — определяющее нечеткое верхнее ограничение. Оценки этих величин выглядят следующим образом:

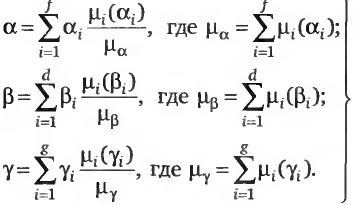
(11.10)

В (11.10) получены некие приближенные средневероятные оценки средней наработки на отказ а, а также нижней β и верхней γ границ диапазона, в котором, по мнению экспертов, должно лежать истинное значение Θ средней наработки на отказ. Если

(11.11)
то полученная оценка а ≈ θ может считаться удовлетворительной и процедура оценки неизвестной наработки на отказ элемента по экспертным заключениям завершается.

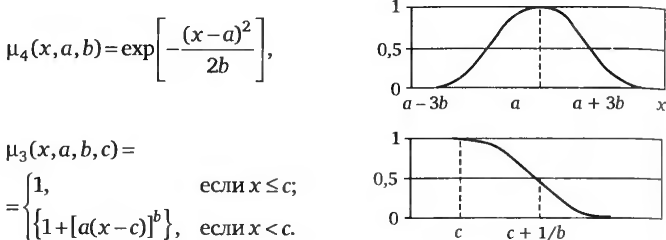
Рис. 11.5. Примеры способов построения функций принадлежности [131]

Если неравенство (11.11) не выполняется, то требуется уточнение оценок θ. Это можно сделать, используя типовые виды функций принадлежности, применяемые в теории нечетких множеств [131], приведенные на рис 11.5.
По найденным значениям α, β, γ строим функции принадлежности в соответствии с формулами, приведенными на рис. 11.5. Используя μ4 (χ, а, b), при условии, что b=-1, а=α получаем следующую функцию принадлежности для нечеткой цели А:

(11.12)

Поведение функции принадлежности μΑ(z) отражает реальную ситуацию, состоящую в том, что чем дальше от общей коллективной оценки, определяющей нечеткую цель, находится оценка отдельного взятого эксперта, тем меньшее значение функции принадлежности отвечает ей.
Нечеткое нижнее ограничение В можно представить следующей функцией принадлежности:

(11.13)

Эта функция принадлежности получена из μ3(χ, а, b, с) при b=-1. Параметры α и β подбираются по зависимости μi(βί).

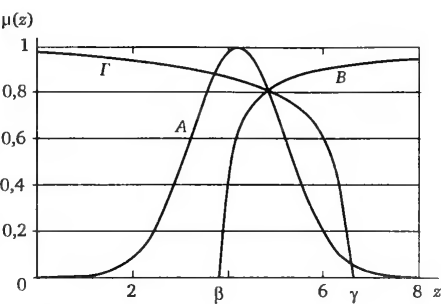
Рис. 11.6. Нечеткое решение по выбору наработки на отказ рассматриваемого элемента с учетом нечетких цели A и ограничений Г и В
Поведение функции принадлежности μΒ(z) (рис. 11.6) отражает реальную ситуацию, состоящую в том, что чем дальше (вправо по графику) от общей коллективной оценки, определяющей нечеткое нижнее ограничение, находится оценка отдельного взятого эксперта, тем большее значение функции принадлежности отвечает ей, так как при увеличении Ζ возрастает число экспертов, уверенных в том, что элемент откажет именно после достижения данной наработки на отказ.
Нечеткое верхнее ограничение Г можно представить в виде следующей функции принадлежности:

(11.14)

Поведение функции принадлежности μΓ(z) (рис. 11.6) отражает реальную ситуацию, состоящую в том, что, чем дальше (влево по графику) от общей коллективной оценки, определяющей нечеткое верхнее ограничение, находится оценка отдельного взятого эксперта, тем большее значение функции принадлежности отвечает ей, так как при уменьшении z возрастает число экспертов, уверенных в том, что элемент откажет именно до достижения данной наработки на отказ.
Далее, в зависимости от требований к качеству результата оценок наработки на отказ можно поступить двумя способами:

1. пусть оценщика устраивает ситуация, когда наилучшая оценка θ выбирается из всех возможных, удовлетворяющих или цели А, или нижнему ограничению В, или верхнему ограничению Г, или любому их сочетанию, т.е. или и А, и В, или и В, и Г, или и А, и Г, или и А, и В, и Г. Тогда строится функция принадлежности вида

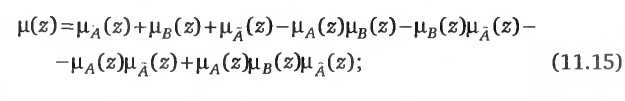
1. если оценщику требуется получить наилучшую оценку, удовлетворяющую только вместе и цели А, и нижнему ограничению В, и верхнему ограничению Г, то строится функция принадлежности вида

Если какая-либо из лингвистических переменных (А, В, Г) отсутствует, то в формуле (11.15) соответствующей функции принадлежности присваивается значение 0 для всех z, а в формуле (11.16) — значение 1 для всех z.
Вне зависимости от выбора [(11.15) или (11.16)] находят

Значение z из (11.17), доставляющее максимум функции μ(z), является наилучшей оценкой наработки на отказ θ, и может быть разным для функций принадлежности, определяемых по

1. или (11.16).

Функция принадлежности, определяемая по (11.15), является более размытой, чем эта же функция, определяемая по (11.16). Поэтому, если требуется оценить максимальный диапазон значений, внутри которого может оказаться истинное значение наработки на отказ θ, следует воспользоваться (11.15). Если же необходима наиболее точная оценка, удовлетворяющая всем требованиям А, В и Г, следует применить (11.16).
Таким образом, приведенная методика позволяет использовать не только четкую количественную информацию по отказам оборудования, но и качественную информацию, содержащую, например, только предположения о причинах отказа или о типе отказавшего элемента.
В заключение отметим, что нечеткие модели можно использовать и для описания неопределенностей в вероятностном анализе, однако нечеткие вычисления отличаются от вероятностных математически и концептуально и более соответствуют случаям, когда плотности распределения вероятностей неизвестны и оцениваются субъективно.