9.2. МЕТОДЫ И МОДЕЛИ АНАЛИЗА НАДЕЖНОСТИ ТРАНСФОРМАТОРОВ
В настоящем параграфе рассматриваются методы и модели определения интенсивности отказов, вероятности безотказной работы и средней наработки до отказа на основании данных по отказам трансформаторов в эксплуатации. Вопросы формирования однородных и достаточных выборок подробно освещены в литературе по математической статистике и здесь не описываются.
В эксплуатации находятся трансформаторы различных годов ввода в работу. Наработки колеблются от 1 года и менее до 20-30 лет и более. Выборки одного года ввода в эксплуатацию, как правило, непредставительны. Поэтому можно применить следующий прием. Трансформаторы различных годов ввода в эксплуатацию сдвигаются по оси времени в нулевую точку, от которой и ведется отсчет времени. Такая модель позволяет для различных наработок t1, t2, .ti получить соответственно выборки с количеством трансформаторов n1, n2,...ni. Отдельно взятая выборка по наработке ί; может рассматриваться как план испытаний [NUT]. Действительно, согласно плану [NUT] одновременно испытывают N объектов, отказавшие во время испытаний не восстанавливают и не заменяют, испытания прекращают по истечении времени испытаний или наработки Т для каждого неотказавшего объекта. Недостатком такого метода является различная точность оценки исследуемого параметра на временных отрезках.
При плане испытаний [NUT] оценка интенсивности отказов статистически определяется отношением


Наиболее простым и наглядным методом определения интенсивности отказов является табличный [163]. Однако при большом количестве простых испытаний (эксплуатация единицы трансформаторного оборудования рассматривается как простое испытание) этот метод становится громоздким. Ниже предлагается матричный метод обработки статистических данных [164], который кроме наглядности и сокращения количества таблиц позволяет относительно просто записать аналитическое выражение для определения интенсивности отказов.
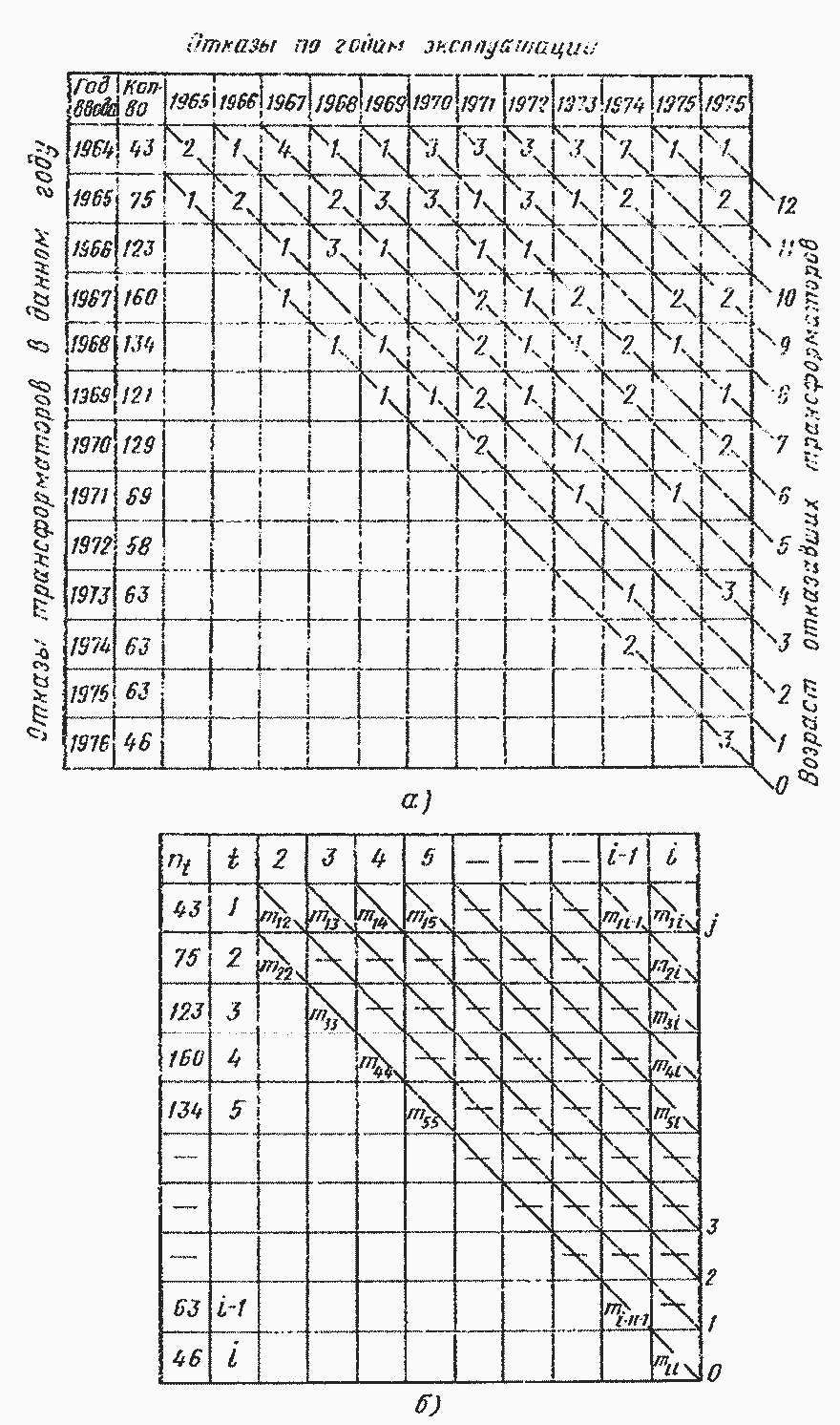
На рис. 9.1, а на примере трансформаторов Ι-П габаритов показана матрица отказов по годам эксплуатации. Строка данной матрицы соответствует отказам трансформаторов рассматриваемого года ввода по годам эксплуатации, а столбец - отказам в данном году трансформаторов различных годов ввода в эксплуатацию. Диагональ такой матрицы дает общее количество отказов трансформаторов в каком-то возрасте. Обозначив время через t (1, 2,..., i), ввод по годам - ni, количество отказов - т с двумя индексами, соответствующими номерам строки и столбца, и присвоив номера диагонали от 0 до j, матрицу можно переписать так, как показано на рис. 9.1, б. Тогда для определения интенсивности отказов на интервале Δt, равном 1 году для отрезка времени 0-j можно записать
(9-2)
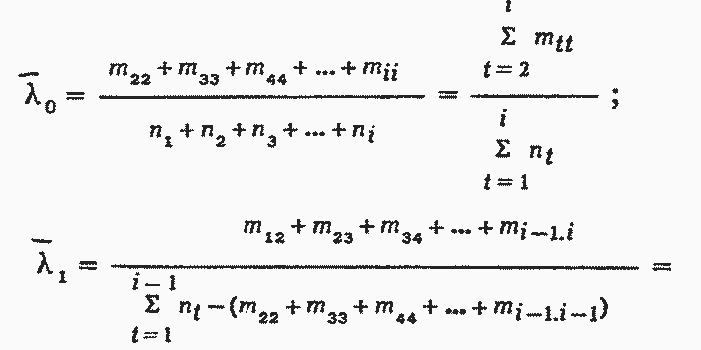
Рис. 9.1. Матрицы отказов трансформаторов по годам эксплуатации

Существует несколько методов определения закона распределения на основании экспериментальных данных:
построение гистограммы и сравнение ее с теоретической кривой плотности вероятности;
построение экспериментальной функции распределения и сравнение ее с теоретической F(t);
построение экспериментальной функции Φ(t) на вероятностной бумаге различных типов распределения;
определение коэффициента вариации и по нему закона распределения;
сравнение экспериментальной зависимости![]() с теоретической.
с теоретической.
Названные методы подробно рассмотрены в [94], где для каждого из них приводятся соответствующие таблицы теоретических функций, функций плотностей различных распределений, таблицы различных шкал вероятностной бумаги, таблицы коэффициентов вариации и таблицы интенсивностей отказов.
Ниже более подробно рассматривается, как один из наиболее простых и наглядных, метод построения экспериментальной функции на вероятностной бумаге для различных законов распределения случайной величины.
Ниже приведены экспериментальные данные по определению интенсивности отказов для трансформаторов одного из предприятий электросетей.
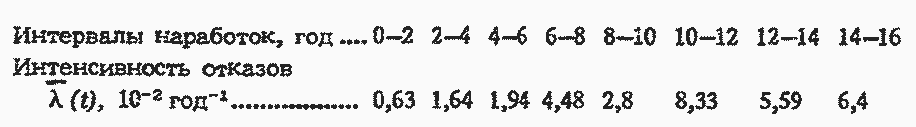
На вероятностной бумаге распределения Вейбулла-Гнеденко была построена экспериментальная функция Ф(t)=1 - е-λ(t) (рис. 9.2).
Функция F(t) распределения Вейбулла-Гнеденко записывается в виде
![]() где а, b и с - соответственно параметры масштаба, формы и сдвига.
где а, b и с - соответственно параметры масштаба, формы и сдвига.
Поскольку выборка времени работы трансформаторов до первого отказа не является полностью определенной, то рассчитать параметры закона аналитически не представляется возможным. Поэтому параметры а и b определены графически по рис. 9.2.

Рис. 9.2. Экспериментальная функция Ф (t) на вероятностной бумаге распределения Вейбулла—Гнеденко
Отказы трансформаторов начинаются с момента ввода в эксплуатацию, следовательно, параметр сдвига с равен нулю.
Определив графически а и b, необходимо проверить согласие наблюдений t1, t2, t3,..., tm с распределением Вейбулла- Гнеденко.
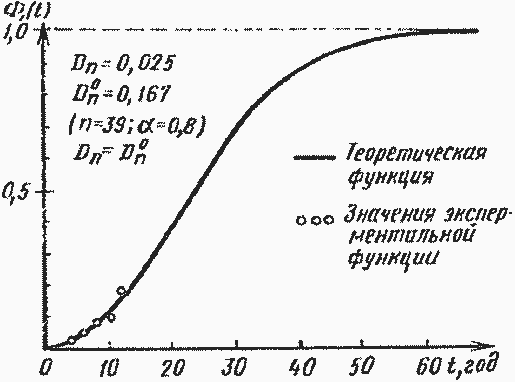
Рис. 9.3. Теоретическая функция распределения Вейбулла—Гнеденко и ее согласие по критерию Колмогорова со значениями экспериментальной функции на интервал наработок 16 лет
Для проверки согласия экспериментального и теоретического закона воспользуемся известным критерием Колмогорова Dn° [14]. Если максимальное расхождение между экспериментальной и теоретической функциями Dn меньше Dn°, отвечающей заданной доверительной вероятности а, то следует принять согласие хорошим.

