Методика оценки влияния наработки на надежность.
В п. 6.3.2 была предложена достаточно универсальная методика оценки влияния различных режимных факторов на надежность энергетического оборудования. В состав этих режимных факторов входила и наработка t. При достаточно обширном объеме эксплуатационных данных по отказам или даже отдельным типовым повреждениям оборудования могут быть использованы отдельные идеи этой методики.
Ниже в виде иллюстрации определяется влияние наработки на параметр потока распушений крайних пакетов сердечника статора генераторов.
Искомая величина определяется в виде
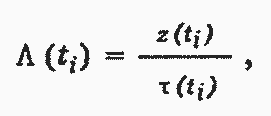(6.86)
где τ(ti) — суммарная наработка генераторов рассматриваемого типа в течение интервала наработки от (ti-0,5Δti) до (ti+ 0,5Δti); ∆(ti) - число случаев распушений, обнаруженных в течение того же интервала наработки. Определенный таким образом параметр Λ(t) является случайной величиной, распределенной по биномиальному закону. Это обстоятельство может быть использовано для оценки доверительных интервалов ∆(t). Этот способ, соответствующий первой стадии универсальной методики, позволяет непосредственно построить эмпирическую зависимость.
Определение аналитической зависимости здесь уже не столь универсально и в значительной степени опирается на характер полученных эмпирических зависимостей ∆(t). В случае распушения крайних пакетов и для ряда других типовых дефектов значение ∆(t) с ростом наработки сначала увеличивалось, а затем уменьшалось. Для сглаживания эмпирических зависимостей Р.Л. Геллером была предложена следующая формула:
(6.87)
Константы λ, т, п определяются следующим образом. Строится плоскость в трехмерном пространстве параметров ln ∆(t), ln t и t:
(6.88)
где
, а затем величины а, m, п определяются как коэффициенты регрессионной зависимости (6.88), имеющие интервальную оценку. С помощью этих величин строится сглаженная зависимость (6.87).
Предложенная методика эффективна, когда информационные массивы насчитывают многие десятки или даже сотни событий. Для сравнительно редких повреждений и отказов она непригодна. Для случая малых выборок Р.Л. Геллером предложена другая методика анализа динамики изменения показателей надежности.
Пусть F (t) есть вероятность появления некоторого типового отказа (т. е. отказа из-за типового дефекта) за время t. Появление отказа на j-м агрегате в момент времени tj свяжем с плотностью вероятности f(tj), где функции f(t) и F(t) подчиняются соотношению 318 где b, Τ - параметры закона Вейбулла, подлежащие определению.
Закон Вейбулла находит чрезвычайно широкое применение в технике и легко позволяет описать как возрастающие, так и убывающие и стабильные потоки отказов. Отмечается, что этот закон, в частности, применим в тех случаях, когда отказ наступает вследствие усталостного разрушения [94].
Подставляя выражения (6.91) в формулу (6.90), получаем
В частном случае при экспоненциальном распределении (b=1) наработка до отказа будет
При b > 1 параметр потока отказов увеличивается со временем, при b < 1 - уменьшается.
Приближенная методика выбора оптимального срока службы оборудования.
Из общих соображений следует, что рост ненадежности оборудования уменьшает его моральный срок службы, т. е. срок службы, с превышением которого эксплуатация становится неэкономичной. Сформулируем оптимизационную задачу, позволяющую при некоторых допущениях решить этот вопрос достаточно строго.
Будем учитывать следующие виды затрат: приведенные затраты на замену оборудования Сз и затраты, связанные с восстановительным (послеаварийным) ремонтом. Затраты, связанные с предупредительными ремонтами, будем считать не зависящими от наработки и не будем учитывать. Из дальнейшего будет видно, что последнее ограничение несущественно и может быть легко учтено введением дополнительных слагаемых затрат.
Будем считать, что затраты на восстановительный ремонт пропорциональны времени восстановительного ремонта, причем среднегодовое время восстановительного ремонта Tв(t) является известной функцией наработки t. Примем, что наработка эксплуатируемого однотипного оборудования распределена равномерно. Тогда, задавая срок службы θ, получим следующие среднегодовые затраты, связанные с эксплуатацией
Пример выбора оптимального срока службы генератора. В табл. 6.6 приведены результаты расчетов, иллюстрирующие выбор оптимального срока службы генераторов θ0. Использовались удельные величины
, значения которых приняты:
Величины То (начальное среднегодовое время вынужденных простоев генератора), t2 (срок удвоения среднегодового простоя) и параметр п (крутизна зависимости параметра потока отказов от наработки) варьировались. Дополнительно приведены расчетные величины Ткр - среднегодовое время вынужденных простоев при оптимальном сроке службы.
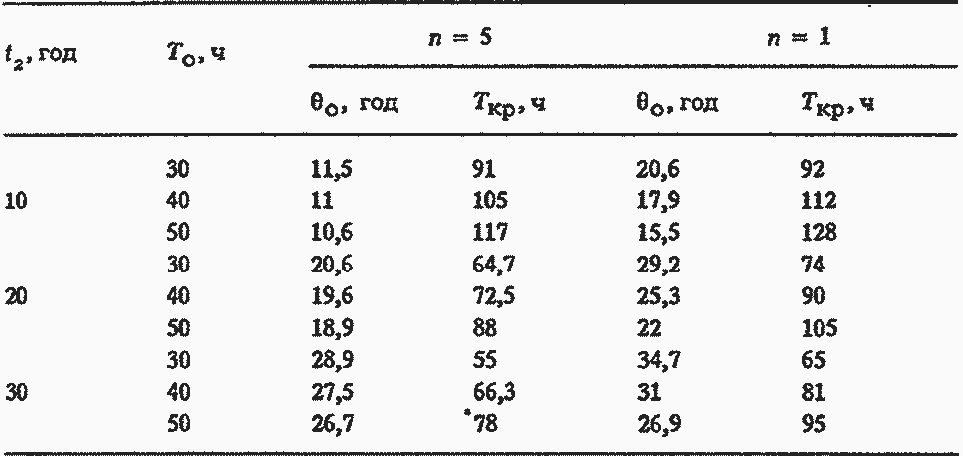
Из табл. 6.6 видно, что основное влияние на оптимальный срок службы θ0 оказывает параметр t2. При малом значении t1 возрастает роль крутизны характеристики λ(t). Величина То влияет на θο сравнительно мало (особенно для крутых характеристик λ(t).
Анализ значений Ткр показывает некорректность интуитивного представления, сформулированного в § 6.1, что оптимальный ресурс близок к значению наработки, при котором показатели надежности резко ухудшаются. При фиксированных показателях То и t2 значение Ткр мало зависит от крутизны характеристики λ(t) (особенно для малых значений t2). Можно также отметить, что диапазон значений Ткр достаточно широк, т. е. выбор оптимального срока службы по достижении некоторого нормированного уровня надежности бесперспективен.
