Надежность систем энергетики - Выбор оптимальных режимов переменной нагрузки тепловых блоков

6.3.2. ВЫБОР ОПТИМАЛЬНЫХ РЕЖИМОВ ПЕРЕМЕННОЙ НАГРУЗКИ ТЕПЛОВЫХ БЛОКОВ

Методика оценки влияния маневренности на надежность тепловых блоков. Количественные характеристики влияния маневренности на надежность тепловых блоков не удается получить методами активного эксперимента путем наблюдений за ’’блоками-лидерами” [95-97]. Гораздо большие возможности дают методы, рассматривающие совокупность эксплуатационных прецедентов как обширный экспериментальный материал, который может быть положен в основу анализа связей между показателями маневренности и надежности.
В качестве параметров, характеризующих надежность блоков, приняты параметр потока отказов λ, продолжительность восстановительных ремонтов одного агрегата в течение рассматриваемого календарного года Тв, а также продолжительности капитальных, средних и текущих ремонтов одного агрегата в течение года Тк, Тс и Тт.
В качестве количественных характеристик пусков-остановов использованы полная частота пусков ω и накопленное к концу каждого календарного года число пусков Ν. В качестве меры частичной разгрузки агрегата принят обобщенный показатель А, отображающий глубину разгрузки блока:
(6.59)
где _- средняя мощность блока в рассматриваемом календарном году; Рном _ номинальная мощность блока. Кроме того, в показатели маневренности включалась наработка t.
Собранные данные группировались по мощности блока, параметрам пара (докритические или сверхкритические) и виду топлива (пылеугольные или газомазутные блоки). Процедура установления связей между параметрами надежности (λ, Тв, Тк, Тс, Тт) и показателями маневренности (ω, N, A, t) разбивалась на две последовательные стадии. На первой стадии, носившей качественный характер, для каждого из показателей маневренности устанавливалось только наличие или отсутствие его влияния на надежность. На второй стадии определялось количественное описание связей каждого из параметров надежности с влияющими на него показателями маневренности. Методика статистического анализа на первой стадии достаточно универсальна и заключается в следующем. Пусть проверяется влияние ряда показателей маневренности хi(i=1·m) на некоторый параметр надежности х0. Отберем из имеющихся данных все значения показателя надежности х0, попавшие в диапазон хi±0,5Δхi(ί=1·m).  Найдя закон распределения случайной величины х0, можно получить оценку математического ожидания х0 и границы доверительных интервалов этого показателя в выбранной точке.
Повторяя описанную процедуру в ряде других точек пространства переменных хi и сопоставляя границы доверительных интервалов, можно проверить влияние каждого из параметров хi(ί=1·m) на показатель надежности х0. Если доверительные интервалы х0 при различных значениях х, и фиксации остальных (т-1) показателей на различных уровнях не перекрывались, параметр х, влияет на показатель надежности х0. При отсутствии влияния хi на х0 этот показатель исключается из рассмотрения.
Как правило, параметры надежности распределены по экспоненциальному закону и являются функцией не более чем двух аргументов.
Для блоков разных типов и мощностей характер зависимостей оказался различным. В качестве примера приведем качественное описание зависимостей, полученных для пылеугольных блоков мощностью 300 МВт:
(6.60)
Для получения количественного описания связей типа (6.60) не пригоден классический регрессионный анализ, так как случайные параметры надежности и ремонтопригодности распределены не по нормальному закону. В этих условиях можно использовать аппарат непараметрического регрессионного анализа [98]. Поясним методику [98] на примере парной регрессии между переменными и и ν'.
Пусть имеется п заданных значений аргументаι,
каждому из которых соответствует случайная величина иi(i=1x n). В качестве величин берутся средние значения соответствующих показателей маневренности и надежности, принадлежащих некоторому элементарному параллелепипеду. Коэффициенты регрессионной зависимости вида и=а+βν (6.61)
определяются следующим образом. Предположим, что все ν, разные и пронумерованы в порядке их возрастания:

Здесь параметры T1, T2, T3 означают соответственно Тв, Τκ, Тс, т. е. продолжительности ремонтов определенного типа. Многие константы в формулах (6.66) равны нулю, что означает отсутствие соответствующих связей. Следует отметить, что параметры λ и Тв оказались сильно коррелированными и одинаковой структуры.
Для отдельных элементов блока не имеет смысла искать влияние на продолжительность плановых ремонтов Тк, Тс. Поэтому проверялась связь между параметрами надежности λ, Тв и показателями маневренности Ν, А, а также наработкой t. Теми же методами, что и для блока в целом, удалось выявить эти связи для котлов, но не удалось для турбин и генераторов. Это не означает, что таких связей для турбин и генераторов не существует, а свидетельствует лишь о том, что на ограниченном статистическом материале об отказах турбин и генераторов поиск достаточно достоверных связей подобными методами бесперспективен. Нужны другие методы с дополнением статистического анализа техническим, с более детальным рассмотрением причин отказов, привлечением понятия дефектов. Метод именно такого типа уже списан в п. 6.3.1 и дополнительно будет проиллюстрирован в п. 6.3.3.
Оптимизация режимов переменной нагрузки с учетом экономичности и надежности генерирующего оборудования. Изменение режима работы тепловых электростанций можно осуществить как путем отключения части энергоблоков в резерв, так и путем уменьшения нагрузки работающих энергоблоков. Задаче выбора оптимального состава работающих агрегатов посвящено большое число работ, однако, как правило, они используют критерий минимума расхода условного топлива [99]. Ущерб от уменьшения ресурса, удлинения и удорожания ремонтов при решении сформулированной задачи обычно не учитывается, а достоверные данные, которые позволили бы количественно оценить этот ущерб, отсутствуют. Между тем, как отмечается в [100], ’’имеются основания полагать, что для мощных энергоблоков пренебрежение этим важным фактором недопустимо и пуски-остановы энергоблоков с целью достижения незначительного эффекта экономии топлива необоснованны”.
Результаты, полученные в первой части п. 6.3.2, позволяют достаточно достоверно учесть и фактор надежности. Следуя [99, 100], запишем условие выгодности останова i-го теплового блока энергосистемы с учетом влияния надежности:

отключений в резерв, тем выше использование остающихся в работе блоков. С помощью простейшей модели покрытия переменной части нагрузки электростанции (упрощенный суточный график электростанции, однотипность условий использования агрегатов и т. д.) можно получить необходимые количественные соотношения. В первом приближении эту связь можно представить как линейную в виде

(6.69)
где k - коэффициент, зависящий от отношения минимальной нагрузки электростанции к максимальной и длительности ночного провала нагрузки.
Пренебрегая аварийными остановами текущего года, можно записать

(6.70)
где Νο — число пусков-остановов, накопленных к началу текущего года (накопленные ранее пуски).
Подставляя (6.68) и (6.70) в (6.66) и учитывая, что каждый пуск-останов текущего года переходит затем в группу накопленных ранее пусков, получим следующее выражение для величины ∆tj - увеличения ежегодной длительности простоя в ремонте j-го типа, приходящегося на каждый пуск-останов:


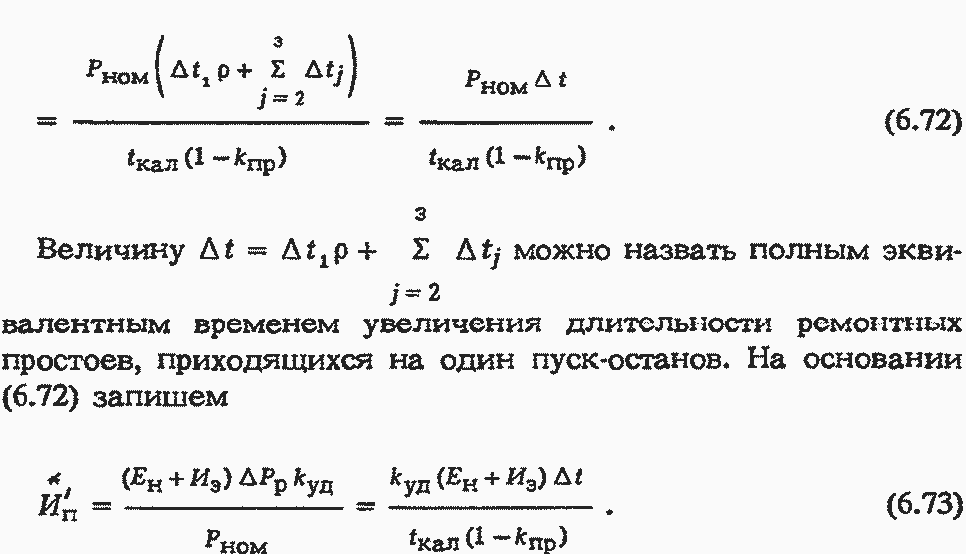
В формулах (6.72) и (6.73) использованы те же величины, что и в формулах (6.22) и (6.27).
Зная величину Ип, можно выбирать оптимальный состав агрегатов по программам ВНИИЭ В-2 и В-3. Такой способ целесообразен для выполнения оптимизационных расчетов в конкретной ЭЭС и получения практических рекомендаций. Однако для выяснения общих тенденций, связанных с учетом влияния маневренности на надежность, этот путь мало информативен. Поэтому введем ряд упрощающих допущений и получим более наглядные условия, позволяющие без громоздких расчетов сделать вывод о целесообразности той или иной стратегии маневрирования.
Примем, что относительный прирост любого из агрегатов системы ε, уменьшается с уменьшением нагрузки агрегата и, следовательно, и относительный прирост системы b монотонно уменьшается по мере разгрузки агрегатов и уменьшения суммарной нагрузки системы. Примем также, что в силу вышеизложенного допущения и условий экономичного распределения нагрузок между агрегатами относительный прирост энергосистемы b связан с относительным приростом отдельных агрегатов εi следующим образом:
если агрегат полностью загружен, т. е. его мощность максимальна, то
(6.74)

получим условия оптимизации стратегии маневрирования в форме, наиболее удобной для выявления общих тенденций. Останов блока без его разгрузки (режим частых пусков-остановов) оптимален, если выполняется условие

Таблица 6.5

1 Здесь и далее стоимостные оценки даны в ценах до 1988 г.

На рис. 6.5 представлены построения, отражающие проверку условий (6.82) - (6.84) для двух электростанций с пылеугольными блоками мощностью 208 МВт. Кривые 1, 2 представляют зависимости правой части соотношения (6.83) от относительной мощности.

Построения, представленные на рис. 6.6, характеризуют групповой анализ совокупности пылеугольных блоков мощностью 200 МВт. Кривые 1, 2 повторяют соответствующие зависимости рис. 6.5, кривые 3, 4 описывают нижнюю и верхнюю границы (с доверительной вероятностью 0,9) зависимости (dq/dP) для совокупности пылеугольных блоков мощностью 200 МВт. Видно, что при неучете фактора надежности выполняются условия (6.82) (кривая 4) или условия (6.83) (кривая 3), т. е. целесообразны остановы блоков либо без предварительной разгрузки, либо с разгрузкой до Р(0)≈0,9. При учете фактора надежности (кривая 2) выполняются условия (6.84), т. е. для всей совокупности пылеугольных блоков мощностью 200 МВт оптимален режим глубокой разгрузки.
Анализ других групп блоков - газомазутных блоков мощностью 200 МВт, пылеугольных и газомазутных блоков мощностью 300 МВт - показал, что во всех этих случаях справедливы результаты, полученные для пылеугольных блоков мощностью 200 МВт. Остановы блоков с частичной разгрузкой или без нее были бы целесообразны только в том случае, если бы маневренность не влияла на надежность. С учетом фактора надежности во всех рассмотренных вариантах оптимален режим глубокой разгрузки блоков.
Глубокая разгрузка блоков до минимума диапазона регулирования является основным способом маневрирования, принятым в эксплуатации. Таким образом, выполненный анализ теоретически обосновывает оптимальность наиболее распространенной на практике стратегии маневрирования, хотя при этом и не достигается максимума экономии топлива.