5.2.3. МОДЕЛИРОВАНИЕ НАДЕЖНОСТИ ДЛЯ ВЫСШИХ УРОВНЕЙ ИЕРАРХИИ ТЕРРИТОРИАЛЬНОЙ ИЕРАРХИИ СЭС-П
Модели, методы и показатели надежности. Состояние информационной базы высшего уровня иерархии СЭС-П более благоприятно для использования точных и сложных математических моделей надежности.

Для модели надежности элемента это означает дополнительную возможность учета: 1) состояния предупредительного ремонта (это состояние обозначается верхним индексом Р), учитываемого в случаях, когда предупредительные ремонты электротехнического и технологического оборудования не совмещаются; 2) состояния ненагруженного резерва (четвертое состояние); 3) ограниченности восстановления.
Действия устройств релейной защиты и автоматики учитываются при описании условий возникновения отказа и в показателях надежности коммутационной аппаратуры.
Для модели надежности системы это означает учет: трех способов восстановления системы после отказа элемента - автоматическими и ручными переключениями или ремонтом; порядка возникновения отказа элемента. Первое обозначается второй цифрой нижнего индекса в функции неработоспособности системы (j=1; 2; 3 для восстановления автоматическими и ручными переключениями или ремонтом) и в состоянии элемента в минимальном сечении. Второе обозначается i, а сам порядок - местом элемента в сечении (первичный отказ - первое место, вторичный - второе и т. п.).
Для усложненной модели предлагаются и усложненные методы, в частности две группы: топологические и логико-топологические. Первые позволяют получить точное решение по графу состояний, как правило, для локальной системы, вторые - по логической функции системы любой размерности. Из топологических методов представлены два - один для графа состояний цепочечного типа (элементы системы равнонадежны), другой для графа состояний типа сети (элементы как равно-, так и разнонадежны). Из логико-топологических представлен специальный метод для приближенного анализа надежности реальных систем.
Графоаналитический метод расчета надежности равнонадежных локальных систем предлагается для систем, состоящих из равнонадежных элементов бинарной модели, граф состояния которой может быть представлен схемой гибели-размножения.

а время восстановления - по времени нахождения системы в


Для простой системы с неограниченным восстановлением показатели надежности рассчитываются следующим образом:

В табл. 5.5 указаны приближенные значения показателей надежности для ограниченного набора систем данного типа.
Графоаналитический метод расчета надежности разнонадежных локальных систем. Метод иерархически занимает промежуточное положение между графотопологическими [75, 75] и аналитическими [74] методами. Система задана не логической функцией, а графом переходов системы из состояния в состояние, а показатели надежности вычисляются так же, как в аналитических методах, только сама вероятность нахождения в состоянии находится с помощью мнемонического правила, выведенного с помощью топологических методов.


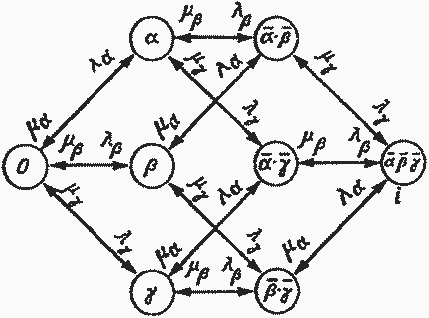
Рис. 5.2. Граф состояний системы
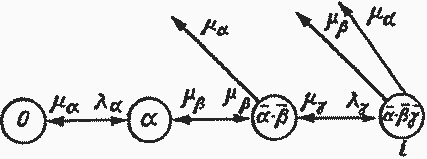
Рис. 5.3. Граф состояний при единственном заданном порядке возникновения отказов
Если состояние отказа системы i определяется не только набором неисправных элементов (α, β, γ) в этом состоянии, но и единственным порядком возникновения отказов (граф состояний приведен на рис. 5.3), то значение P(i) определяется двумя факторами - значениями р этих элементов и коэффициентами возвращения системы в предыдущее состояние при восcтановлении


Рис. 5.4. Граф состояний при задании очередности отказов для а элементов из h
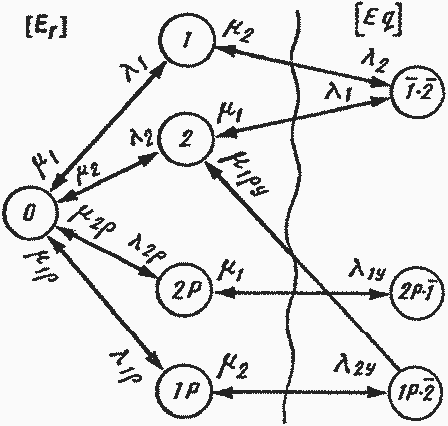
Рис. 5.5. Граф состояний системы, состоящей из двух параллельно соединенных элементов
Решение. Граф состояний системы представлен на рис. 5.5. Подмножества {Еr} и {Eq} разделены волнистой линией. Все состояния {Еq} критичны по всем неработоспособным состояниям элементов.
Процесс нахождения показателей представлен в табл. 5.11.
Логико-топологический метод расчета надежности реальных систем. Реальные системы электроснабжения промышленных предприятий отличаются большой громоздкостью, что практически исключает возможность построения графа состояний системы.
Для расчета надежности более целесообразно использование приближенного логико-топологического метода, подобного предложенному для исследования систем на низших и средних иерархических уровнях.


Аналитические выражения из табл. 5.12, позволяющие итерационным путем найти показатели надежности системы по приближенной функции неработоспособности F, дополняют содержимое табл. 5.8 возможностью учета следующих вариантов усложнения системы: 1) учетом состояний предупредительного ремонта элементов; 2) учетом времени восстановления системы после отказа элементов (это должно быть отмечено в F вторым нижним индексом у элемента: 1 — при восстановлении работы автоматическим переключением; 2 - при восстановлении работы ручным переключением, а обозначение восстановления ремонтом γ= 3 может быть опущено или не иметь обозначения); 3) учетом порядка возникновения отказов (местом отказавшего элемента в минимальном сечении и знаком отказа -* ).

4) при нахождении В использованием только критических состояний (сечений) младших порядков.

Таблица 5.14
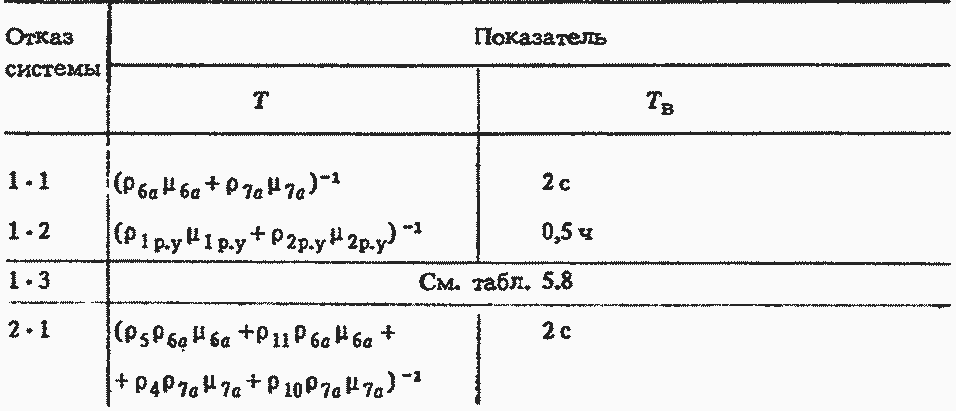

Пример 5.7. Найти показатели надежности подстанции, рассмотренной в примере 5.5, с учетом предупредительных ремонтов элементов для шести отказов работы системы: 1·1, 1·2 и 1-3 - погашение одного из потребителей на время автоматических и ручных переключений или ремонтов соответственно;
- 1, 2-2 и 2-3 - погашение обоих потребителей на все три продолжительности соответственно.
Решение. F для всех отказов системы представлены в табл. 5.13, а выражения для оценки Т и Тв - табл. 5.14.

