6.2. МЕТОДЫ И МОДЕЛИ АНАЛИЗА НАДЕЖНОСТИ ГЕНЕРИРУЮЩЕГО ОБОРУДОВАНИЯ
6.2.1. ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДОВ И МОДЕЛЕЙ АНАЛИЗА НАДЕЖНОСТИ ГО
Методы анализа надежности ГО условно делятся на методы экспертных оценок, моделирования и экспериментальные. Условность определяется возможностью и (или) необходимостью одновременного использования двух или всех методов. Решение о выборе метода принимается на основании поставленной задачи, объема исходной информации и времени, отведенного для ее решения. Во всех случаях используемый подход должен быть эффективным средством ретроспективной оценки событий и инженерного прогноза состояния оборудования. При равенстве достоверности выбирается наиболее дешевый и быстровыполнимый метод.
Метод экспертных оценок. Суть метода в том, что перед экспертом или группой экспертов-специалистов ставится ряд вопросов, касающихся надежности ГО или ГЭ. Для групповой экспертизы возможны две процедуры получения оценок.
Первая наиболее простая, представляет собой зависимый интеллектуальный эксперимент, когда в экспертной группе производятся первоначально поочередные высказывания каждого эксперта и регистрация мнений в порядке выступлений. При этом каждый последующий эксперт высказывает свою точку зрения на поставленные вопросы и мнение по высказываниям предшественников. Вторым этапом экспертной оценки является дискуссия, в которой обсуждаются все высказывания. Третий этап - составление экспертного заключения. Эффективность дискуссии оценивается не по критическим замечаниям, а по конструктивным идеям, высказанным в процессе обсуждения проблемы.
Вторая, более сложная и длительная по исполнению, позволяет лучше использовать интеллектуальный потенциал экспертов и получить более строгий результат экспертизы. В круг обязанностей каждого эксперта входит ранжирование объектов экспертизы по значимости (вес свойств и характеристик надежности), анализ исходной информации о состоянии ГО и ретроспективных событиях, определение вида обработки исходных данных, прогноз динамики событий на ближайшую и отдаленную перспективу. Выполнение обязанностей экспертами базируется на статистическом и эвристическом методах.
При статистическом подходе в круг обязанностей экспертов входит:
ранжирование свойств по значимости;
определение среднеарифметических весов характеристик (свойств);
обоснование выбора параметров оценки;
установление аналитической связи между весом характеристики и номером, который она занимает в ранжированной последовательности;
определение вариации (среднеквадратического отклонения от среднеарифметического значения всех характеристик в совокупности). Для заключения выбирается вариант с наименьшей вариацией. В этом случае расхождение мнений экспертов наименьшее.
При эвристическом подходе рассматриваются следующие показатели, характеризующие степень согласованности мнений экспертов:
ранг оценки веса, соответствующего или несоответствующего порядковому номеру (оценивается соответствие веса по значимости свойства или характеристики тому номеру, который присвоен ГО или ГЭ при ранжировке);
сумма рангов;
коэффициент конкордации, отражающий степень согласованности мнений экспертов по всей согласованности свойств или характеристик;
коэффициент парной корреляции (аналог коэффициента корреляции), служащий для определения согласованности (тесноты) мнений экспертов по двум характеристикам;
коэффициент активности, представляющий отношение участвовавших в работе экспертов к общему числу экспертов, назначенных для экспертизы.
Логическая и количественная характеристики перечисленных и некоторых других показателей согласованности мнений экспертов приведены в табл. 6.1.
Экспертное заключение составляется по варианту наибольшей согласованности мнений экспертов. Объективности ради эксперты в период работы не контактируют между собой и не знают мнения коллег. Результаты - оформленные мнения передаются главному эксперту, который анализирует материал и составляет экспертное заключение.
Метод моделирования основан на абстрагировании процессов развития событий и переходов ГО или ГЭ из одного состояния в другое. Различают разновидности моделей: информационные, логические, математические, аналогии и др. Для оценки свойств надежности эффективны математические модели. В зависимости от постановки задачи абстрагирование событий отражает закономерности процесса функционирования ГО путем получения количественных характеристик безотказности, ремонтопригодности, долговечности и сохраняемости в пространстве времени или количества выработанной тепловой энергии и (или) электрической энергии. Основанием для построения математической модели является структурная схема надежности, на которой изображаются функциональные связи между ГЭ, их резервирование и его характер, а также оценивается ремонтопригодность (восстанавливаемый, невосстанавливаемый).


К методам построения математических моделей, характеризующих свойства надежности, предъявляются определенные требования.
Математическая модель безотказности не должна отражать процессы восстановления после отказа. Принимается допущение, что после отказа восстановление происходит мгновенно до состояния, соответствующего исходному (проектному). Наработки времени или энергии между отказами являются случайными и независимыми величинами. Модель должна быть универсальной и пригодной для расчета безотказности при любых условиях эксплуатации ГО (для разных нагрузок, видов топлива, возраста оборудования, мощности и параметров рабочего тела, конструкции и др.) и выборок с любым признаком однородности. При неопределенности исходных условий (неопределенность информации) должны быть использованы модификации модели, позволяющие получить достоверные количественные характеристики безотказности.
Математическая модель ремонтопригодности должна отражать совершенство конструкции ГО в части способности к восстановлению работоспособности после отказа. Времена восстановлений являются случайными и независимыми величинами. Математическая модель должна быть универсальной и пригодной к использованию для выборок с однородными признаками любого ГО или ГЭ. В математической модели не обязательно дифференцирование времени восстановления на составляющие: время отключения оборудования после возникновения отказа, время поиска дефекта, время устранения дефекта, время включения оборудования в работу. Для перечисленных характеристик ремонтопригодности строятся локальные модели, которые здесь не рассматриваются.
Математическая модель долговечности должна обеспечить решение двух задач. В первой оценивается долговечность на основании изменения свойств материалов ГО под действием физических и химических процессов и на этой основе определяется предельная допустимая наработка, при которой риск возникновения отказа равен нулю; связь между процессами на ГО и наработками выражается в конечном счете через величину прочности и ее расходование во времени. Допустимым ресурсом считается наработка, при которой коэффициент запаса прочности К = f(τ) ≥ [К]. При предельном состоянии К=f(t)-0. Отмеченные условия в математической модели соблюдаются при строгой функциональной зависимости между функциями и аргументами, где в качестве аргументов используются количественные характеристики процессов (параметры рабочего тела, цикличность нагрузок, характеристики топлива и др.), а функции - характеристики прочности.
Во второй - математическая модель должна обеспечить определение вероятности изменения текущего состояния величин х1, х2,..., хп, характеризующих отдельные свойства материалов и их изменение под действием условий эксплуатации, где случайные величины х1, х2,..., хп - зарегистрированные результаты диагностики.
Математическая модель сохраняемости близка по смыслу к первой задаче долговечности. Отличие заключается в принципе оценки предельного состояния. Для модели сохраняемости должно соблюдаться условие![]() - проектное значение коэффициента запаса прочности, учитывающее атмосферную коррозию и естественное старение материалов.
- проектное значение коэффициента запаса прочности, учитывающее атмосферную коррозию и естественное старение материалов.
Метод экспериментальных оценок. Основан на фиксировании в любой заданный момент времени с помощью средств диагностики конкретных величин, качественно и количественно характеризующих одно или несколько свойств надежности. При использовании метода с целью получения представительных данных должны быть выполнены следующие условия:
параметры, определяемые экспериментально, должны быть необходимыми и достаточными для оценки свойств надежности;
методы диагностики, используемые для измерения параметров, должны отвечать требованиям метрологии и давать представительную информацию, достаточную для получения выводов;
периодичность диагностики должна обеспечить выполнение условий![]() - обнаруженный дефект;
- обнаруженный дефект;
[Д] - допустимая величина дефекта по нормативно-технической документации.
В общем случае использование всех методов или некоторых из них в зависимости от состояния ГО или ГЭ и имевших место событий при анализе реализуется по алгоритму, приведенному на рис. 6.1. Можно отметить следующие наиболее распространенные признаки однородности выборок:
- единичная мощность блока;
- параметры свежего пара;
- вид топлива (твердое, жидкое, газообразное, комбинированное);
- завод-изготовитель котлов;
- марки котлов;
- завод-изготовитель турбин;
- типы турбин;
- возраст энергоблоков (наработка времени, ч);
- режим работы (базовый, пиковый, полупиковый).
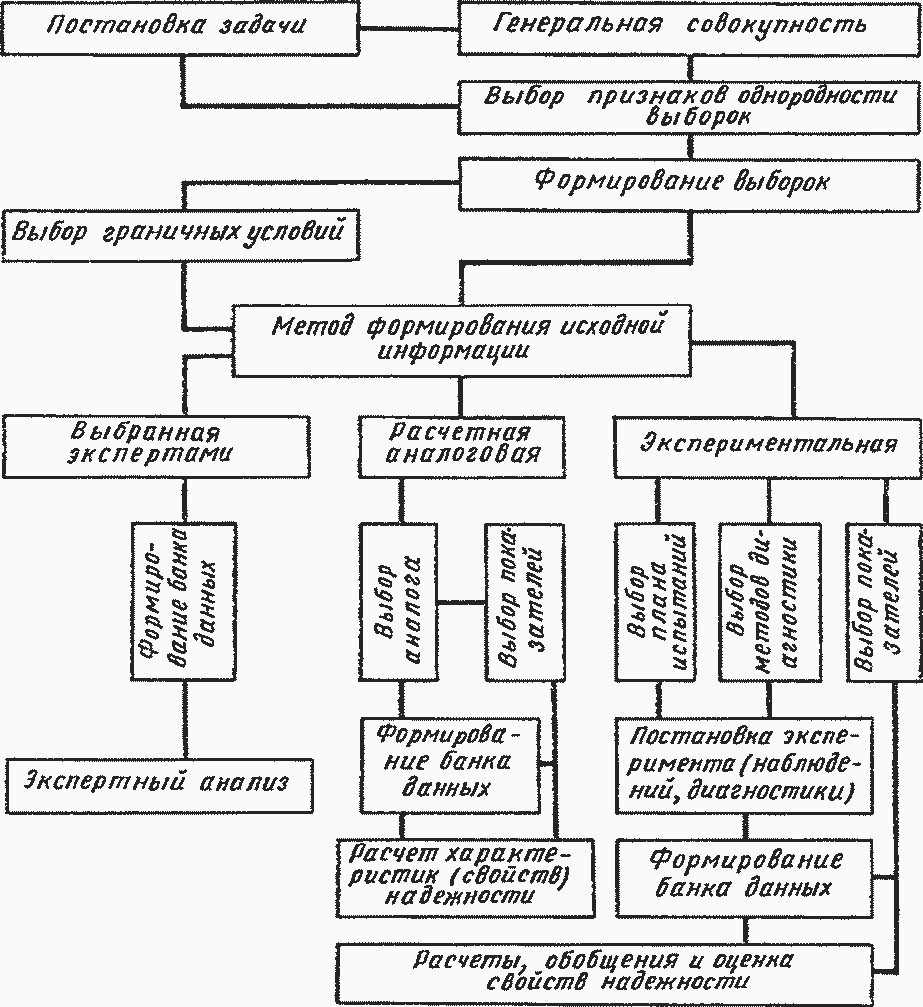
Рис. 6.1. Алгоритм реализации методов анализа надежности ГО, ГЭ
Используются также комбинации признаков, например мощность энергоблока - вид топлива.
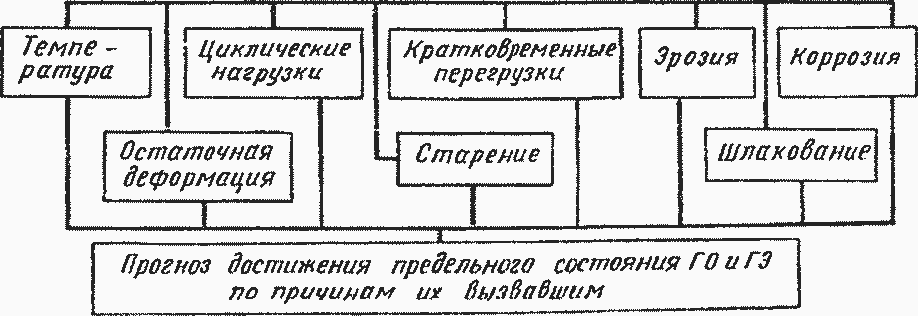
Рис. 6.2. Алгоритм прогнозирования долговечности при проектировании ГО и ГЭ
Распространенными граничными условиями при анализе свойств надежности считайся: интервал времени наблюдения, наработка времени (например, до наработки 105 ч или в интервале 105-1,5-105 ч), число пусков, календарное время работы, группа и количество ГО.
Для прогноза в период проектирования, изготовления и освоения нового оборудования используется алгоритм, показанный на рис. 6.2.
6.2.2. МОДЕЛЬ АНАЛИЗА НАДЕЖНОСТИ ОБОРУДОВАНИЯ С УЧЕТОМ НЕСКОЛЬКИХ ТИПОВ РАБОЧИХ СОСТОЯНИЙ
Для применения технической диагностики, а также других приложений анализ простых систем, т. е. систем, принимающих только два состояния — полностью работоспособное и неработоспособное - недостаточно эффективен. Появление различного рода неисправностей по существу переводит систему из исправного (нормального) состояния в неисправное, так как по мере развития некоторых неисправностей может произойти отказ. Отсутствие же неисправностей является в какой-то мере гарантией безотказной работы. Требуется использовать эти эвристические соображения для построения достаточно строгой математической модели.
Решающим шагом в этом направлении является специальное (узкое) использование термина ’’дефект”, основополагающего для технической диагностики. Согласно терминологии технической диагностики (ГОСТ 15467-79, [101]) под дефектом следует понимать любое несоответствие свойств объекта заданным, требуемым или ожидаемым его свойствам. Сузим данное определение дефекта. Для этого будем считать, что общепринятое определение относится не к дефекту, а к неисправности. Под дефектом же будем понимать только те неисправности, по мере развития которых происходит отказ. В этом смысле термин ’’дефект” очень близок к используемому иногда термину ’’скрытый отказ”.
Применительно к генерирующему или другому оборудованию появление дефекта может непосредственно никак не препятствовать его прямому функционированию. Например, повышенные вибрации обмотки статора турбогенератора не сказываются ни на значении генерируемой мощности, ни на качестве электроэнергии. Однако это потенциальный источник отказа. Поэтому в соответствии с принятыми определениями можно считать, что при полном отсутствии дефектов состояние исправное (нормальное) и отказов быть не может, появление любого дефекта приводит к неисправному (но рабочему) состоянию, развитие дефекта приводит к отказу, т. е. к неработоспособному (нерабочему) состоянию.
Заметим, что для единообразия терминологии настоящего справочника было бы заманчиво отождествить неисправное состояние с частично работоспособным. Однако это некорректно, так как работоспособность в неисправном состоянии может совершенно не теряться. В то же время неисправные рабочие состояния явно отличаются от исправного рабочего состояния. Это дает основание считать, что модель анализа надежности, использующая представленное понятие дефекта, учитывает несколько типов рабочих состояний.
Учитывая стохастическую природу рассматриваемых явлений, остается описать вероятности различных состояний. Будем считать, что появление некоторого дефекта Д, есть случайное событие, причем вероятность его появления за время t описывается функцией распределения Fj(t). Если дефект Дi появляется в момент ί, то в промежутке времени (0, ί) отказа вообще быть не может, а за промежуток времени (ί, θ) этот дефект приведет к отказу с вероятностью Фi (θ - t).
Функции распределения Fi(x), Фi(у) могут быть определены на основании общих соображений и (или) по ретроспективным данным. Заметим, что применительно к дефектам имеется совершенно неудовлетворительная ретроспективная информация, так как дефекты, возникающие в работе, практически не выявляются, а регистрация и обработка данных по дефектам,



Отсюда для относительных величин
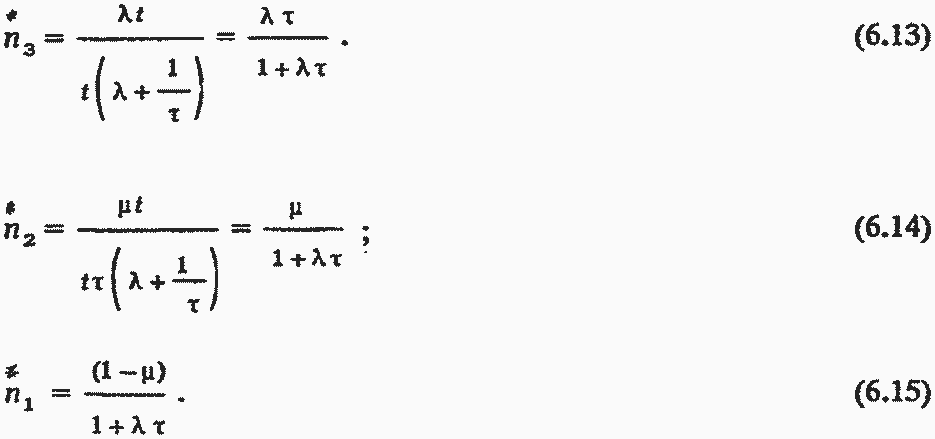
При выводе формул (6.13) - (6.15) допущена некоторая некорректность. Считается, что длительность τ относится только к (n1 +n2) ремонтным циклам, в которых не наблюдался отказ. Если считать, что и длительность цикла с отказом (цикла третьего типа) составляет величину τ, то необходимо дополнительно разделить такие циклы на циклы с одним, двумя, тремя и т. д. отказами, т. е. проделать достаточно сложные выкладки, не предусмотренные формулой (6.4).
Простые соображения позволяют избежать этой сложной работы. Рассматривая в качестве длительности цикла третьего типа только время до первого отказа, можно показать, что в зависимости от фактической средней длительности цикла третьего типа величина λτ лежит в диапазоне
![]()
Правая граница диапазона соответствует нулевой средней длительности цикла третьего типа и формуле (6.13). Левая граница соответствует средней длительности цикла третьего типа, равной τ. Поскольку для дефектов генерирующего оборудования в подавляющем большинстве случаев λτ«1, правая и левая границы диапазона λτ практически неразличимы, можно не считаться с отмеченной некорректностью и использовать формулу (6.13), а также формулы (6.14) и (6.15).
Объединяя (6.15), (6.6) и (6.13), (6.8), учитывая (6.9), получаем уравнения для определения неизвестных величин α0, αд,T0, ТД) по известным τ, λ, μ:
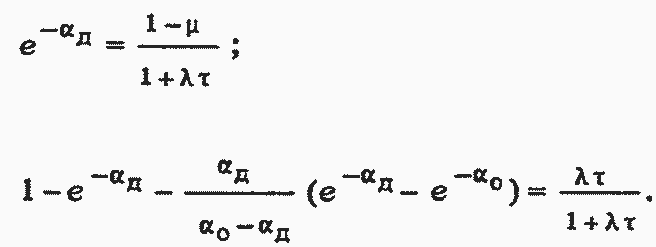
(6.16)
(6.17)
Для дальнейшего анализа будут полезны и соотношения, обратные формулам (6.13) и (6.15):

(6.18)
(6.19)
Способы определения параметров λ для различных дефектов на основе эксплуатационной информации по отказам хорошо разработаны. Строгое определение параметров τ, μ для различных дефектов потребует детального и систематического анализа ретроспективной информации по плановым ремонтам. Для предварительных оценок эти данные можно определять упрощенно на основании экспертных оценок.
Формулы (6.16) и (6.17) позволяют определить собственные параметры расчетной модели на основе ретроспективной информации. Формулу (6.18) можно рассматривать как способ расчета основного типового показателя надежности — параметра потока отказов λ.

