Основные признаки, определяющие специфику рассматриваемого класса систем электроснабжения, учитываемую при выборе оценочных средств и используемых допущений, рассмотрены в п. 5.1. Ниже с учетом сказанного рассматриваются расчетные модели различной сложности, применение которых относится к разным уровням территориальной иерархии СЭС-П.
При выборе указанных моделей учтено категорирование потребителей, которые при этом разделены на четыре группы - особую и три экономические. Для характеристики состояний работы и аварийного ремонта используются вероятностные характеристики. При этом допускается, что восстановление после отказа является неограниченным, полным и осуществляется ремонтом. Особые режимы работы не учитываются. Резервирование считается нагруженным.
Более подробно характер учета указанных условий и особенности моделей и методов оценки надежности рассмотрены в их связи с областью конкретного применения.
5.2.1. МОДЕЛИРОВАНИЕ НАДЕЖНОСТИ НА НИЗШИХ УРОВНЯХ ТЕРРИТОРИАЛЬНОЙ ИЕРАРХИИ СЭС-П
Модели, методы и показатели надежности. В данном случае рассматриваются сети третьего уровня иерархии, соответствующие распределительной сети и непосредственно потребителям. Этот уровень характеризуется ограниченностью, а в ряде случаев и вообще полным отсутствием достоверной информационной базы. Поэтому для этих уровней предлагается сохранение и последующее развитие используемой в настоящее время так называемой опосредованной модели оценки и нормирования надежности.
Опосредованными названы показатели, характеризующие надежность, но по нормативным документам показателями надежности не являющиеся. Их числовое значение подсчитывается непосредственно по схеме или ее описанию и не требует использования математических методов.
Основным опосредованным показателем является категория надежности, которая формализованно оценивает требуемую по условиям технологического процесса степень надежности электроснабжения.
Таким образом, традиционный метод моделирования надежности заключается в определении категории нагрузки по качественному описанию последствий перерыва ее электроснабжения и в построении системы электроснабжения по нормируемым для каждой категории опосредованным характеристикам.
Однако более точные результаты дает применение математических моделей.
Для элементов СЭС это бинарная модель надежности с отказами элементов типа КЗ без учета проведения предупредительных ремонтов. Резервирование - нагруженное, обеспечивается учет мощности источников, пропускной способности элементов и категории (требования надежности) нагрузок.
Все элементы СЭС, которые могут быть отнесены к высоконадежным, или отказы которых не приводят к отказу системы, при моделировании не учитываются. Элементы, учитываемые при моделировании, считаются равнонадежными.
Для системы используется также только бинарная модель, т. е. оцениваются только полные перерывы электроснабжения и только на время ремонта. Не учитываются ограниченность восстановления, особые режимы электроснабжения и повреждаемости и т.п.
Имеют место все допущения, общепринятые при расчете надежности технических систем.
Для анализа надежности на этих уровнях рекомендуются самые простые из групп логико-вероятностных и логико-топологических методов.
Логико-вероятностными методами (ЛВМ) названы методы [69, 70], в которых математические модели надежности элементов и системы описываются с помощью алгебры логики, а показатели надежности - теоремами теории вероятностей, причем и то и другое осуществляется в неявной форме.
Основные достоинства ЛВМ: четкость, однозначность и высокая степень формализации при описании объекта исследования; выполнение оценки, расчета, анализа и оптимизации надежности на единой методической основе; возможность исследования так называемых мостиковых структур.
Расчет надежности с помощью ЛВМ состоит из двух этапов. Цель первого - переход от словесного описания процесса функционирования системы к формализованному; цель второго — количественный учет в формализованно описанной системе показателей надежности системы показателей надежности элементов для нахождения показателей надежности системы.
Логико-топологическими методами (ЛТМ) названы методы [74, 75], в которых математические модели надежности элементов и системы описываются, как и в ЛВМ, с помощью алгебры логики, а на втором этапе, при нахождении показателей надежности систем, используются аналитические выражения, полученные с помощью специализированных топологических методов (ТМ)1.
Достоинством ЛТМ является непосредственное нахождение показателей надежности по логическим функциям, без вычисления полиномов R и Q - вероятностей работоспособного и неработоспособного состояния системы. Недостатком ЛТМ при нахождении точного решения является громоздкость вычисления, так как расчет фактически выполняется не для логических функций, а для формализованно получаемых состояний работы или отказа системы.
Для ЛВМ и ЛТМ возможно на обоих этапах выполнение как точных, так и приближенных действий с оценкой знака и значения погрешности.
Простейшими формами ЛВМ и ЛТМ являются таблицы готовых решений, которые рекомендуются для решения локальных задач анализа надежности, но также могут быть использованы для приближенного анализа крупных систем.
Для более серьезных расчетов рекомендуются в качестве представителя ЛВМ логико-аналитический метод (ЛАМ), а в качестве представителя ЛТМ - упрощенный ЛТМ (УЛТМ).
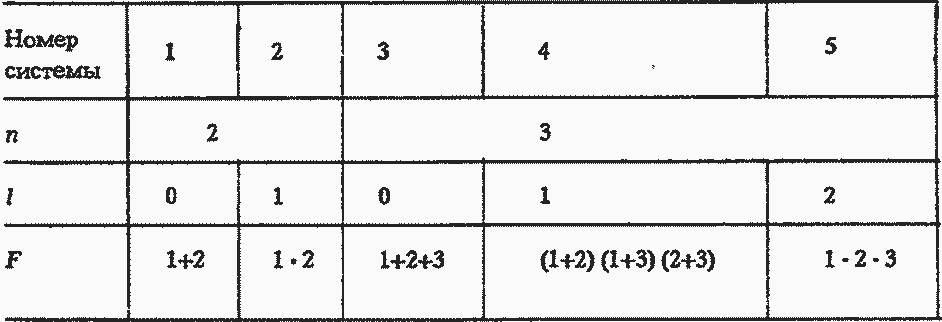
Расчет надежности с помощью таблиц готовых решений. Приближенным ЛВМ могут считаться аналитические выражения, приведенные в табл. 5.2. Они предлагаются для расчета надежности систем, заданных в виде логической функции условий работоспособности системы через условия работоспособности совокупностей отдельных элементов, путем поэтапного преобразования нескольких параллельно или последовательно в логическом смысле соединенных элементов в один эквивалентный элемент.
В зависимости от вида соединения элементов с помощью представленных в табл. 5.2 выражений находятся показатели надежности эквивалентного элемента (любых двух из четырех перечисленных). Расчет заканчивается, когда условия функционирования представлены одним эквивалентным элементом и найдены его показатели надежности.
Важной особенностью расчета является вид условий работоспособности.
Это может быть последовательно-параллельное соединение элементов, т. е. последовательное для элементов так называемого минимального пути [69, 73] и параллельное - для соединения минимальных путей между собой, но только в случае, если полученная логическая функция является бесповторной.
Это может быть параллельно-последовательное соединение элементов, т. е. параллельное соединение элементов так называемого минимального сечения [69, 73] и последовательное соединение самих сечений как для бесповторных, так и для повторных логических функций.

Таблица 5Л
Применение аналитических выражений к бесповторной логической функции дает точное решение, а к параллельно-последовательной повторной - приближенное, завышенное по значению параметра потока отказов системы за счет повторного учета одних и тех же элементов.
Пример 5.1. Рассчитать надежность типовых структур в системе электроснабжения. В качестве таких выбраны типовые системы в n=2+4 и l=0+3 (n - всего элементов; l - количество резервных элементов).
Решение. Наиболее трудоемкая часть решения - логические функции работоспособности - даны в табл. 5.3. Для систем 1-3, 5-6, 9 они даны через минимальные пути, для систем 3, 7, 8 - в параллельно-последовательной форме, так как минимальные пути (последовательно-параллельная форма) являются повторными.
Для n=2, l=0:
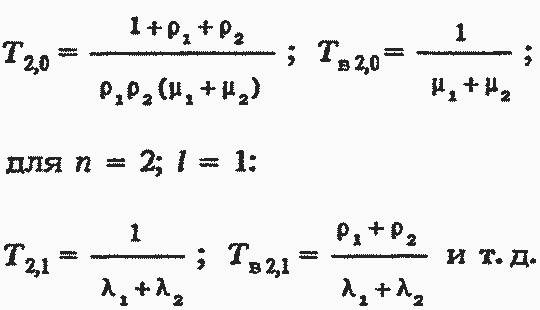
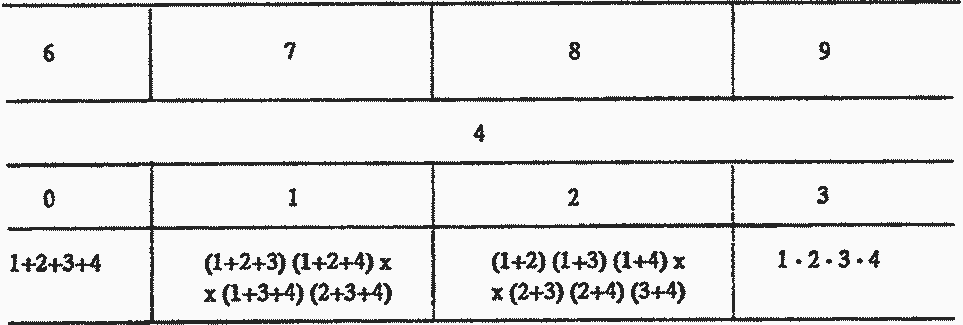

Приближенным ТМ могут считаться аналитические выражения табл. 5.4 (числитель - параметр потока отказов исследуемой системы Ω; знаменатель - интенсивность восстановления системы М; дробь в целом Ω /М = Р - опасность отказа системы). Сама система задается общим числом элементов п, в том числе резервных (резервирование нагруженное) l=0+(n-1); показателями надежности равнонадежных элементов системы λ и μ.
Пример 5.2. Найти показатели надежности системы, состоящей из четырех однотипных элементов (λ, μ), любые два из которых являются резервными (система 8 из табл. 5.3).
Решение. На пересечении столбца l=2 и строки п=4 находим искомые показатели:![]()
5.2.2. МОДЕЛИРОВАНИЕ НАДЕЖНОСТИ НА СРЕДНИХ УРОВНЯХ ИЕРАРХИИ СЭС-П
Модели, методы, показатели надежности. Информационная база среднего (или второго согласно § 5.1) уровня иерархии СЭС-ΓΙ находится в несколько лучшем состоянии по сравнению с низшим третьим уровнем. Поэтому предлагаемые ниже модели дополнены рядом учитываемых факторов по сравнению с предыдущими. Так, для элементов учитывается возможность учета различия показателей надежности, наличие предупредительных ремонтов оборудования, не совпадающих с предупредительными ремонтами технологического оборудования.
Для системы учитывается возможность нескольких разновидностей отказов по тяжести i (полный перерыв и различные ограничения электроснабжения) и по продолжительности j (отказ на время автоматических переключений, ручных переключений и ремонтов). В качестве методов исследования моделей используются ЛВМ и ЛТМ.


Пример 5.3. Найти с помощью ЛАМ показатели надежности систем из примера 5.1.
Решение. Результаты точного расчета представлены в табл. 5.5. Легко проверить, что для бесповторных логических функций решение из примера 5.1 совпадает с найденным.
Логико-топологический метод расчета надежности реальных систем. Показатели надежности системы вычисляются по ее функции неработоспособности2, являющейся разновидностью функций алгебры логики (ФАЛ) и показателями надежности элементов, с помощью следующих выражений:

l* - те элементы из совокупности l, восстановление которых приводит к восстановлению системы; {-}, {+} - подмножество неработоспособных и работоспособных состояний системы соответственно.
1Топологическими методами названы методы, условия функционирования систем в которых представлены графом состояний, а показатели надежности которых вычисляются без составления и решения систем уравнений с помощью различного рода аналитических выражений и мнемонических правил [76].
2 Имеется несколько более сложная модификация метода, предназначенная для нахождения показателей надежности по минимальным путям.
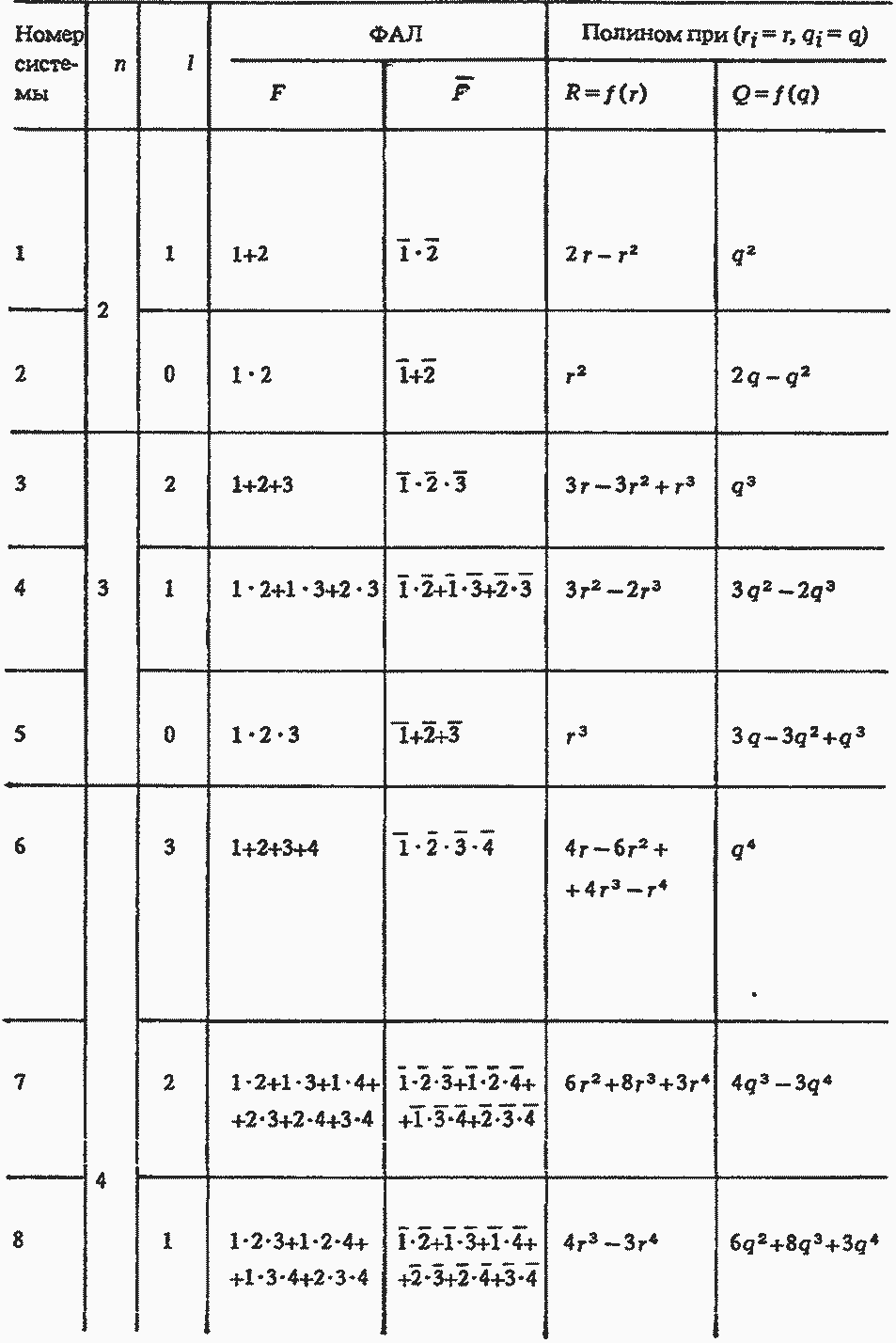



Таблица 5.6


Рис. 5.1. Агрегированная схема двухтрансформаторной подстанции
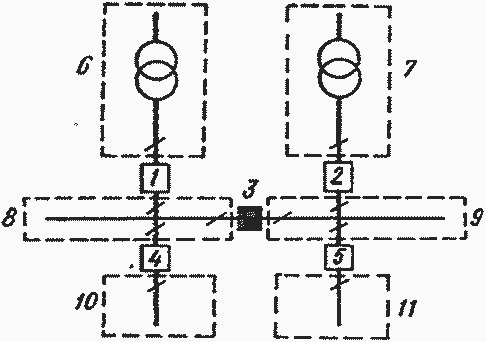
Таблица 5.8

* Опущены двойные отказы.
Пример 5.5. Найти показатели надежности двухтрансформаторной подстанции (рис. 5.1) для двух отказов работоспособности: 1-3-погашения потребителей одной из линий на время ремонта; 2-3 - погашения потребителей обеих линий на время ремонта.
Решение. Агрегируем несколько элементов, расположенных между смежными выключателями (на рисунке показаны пунктиром). Показатели надежности агрегированного элемента находим с помощью аналитических выражений табл. 5.8 (для последовательно соединенных элементов). Пронумеруем агрегированные элементы и найдем приближенную функцию неработоспособности для обоих отказов (табл. 5.9).

