Применение упрощенных расчетных схем сопротивления материалов (тонкий брус) и даже теории тонких оболочек для определения напряжений в таких элементах трубопроводов, как гибы, тройники, корпуса арматуры и др., может привести к значительной погрешности из-за несоответствия формы элементов исходным предпосылкам этих моделей. Численные методы пространственной теории упругости позволяют решать задачу о распределении напряжений в таких элементах трубопроводов в более точной постановке. В настоящее время наибольшее развитие получили такие методы, как метод конечных элементов и метод граничных интегральных уравнений.
Ниже рассмотрено применение метода граничных интегральных уравнений к расчету напряженного состояния гибов и тройников в трехмерной постановке.
Описание алгоритма расчета
Эффективным методом решения трехмерной задачи теории упругости является метод граничных интегральных уравнений (МГИУ) [80]. Основным преимуществом МГИУ по сравнению с другими численными методами механики сплошной среды (в том числе и методом конечных элементов) является снижение на единицу размерности решаемой задачи. Иными словами, решение задачи выполняется только на граничной поверхности, а внутри области уравнения теории упругости удовлетворяются автоматически. Это преимущество особенно ощутимо при расчете толстостенных конструкций, к которым относятся и гибы паропроводов высоких параметров.
Ключевым моментом применения алгоритма является предложенная П. И. Перлиным [81] схема вычисления главного значения сингулярных интегралов. Решение соответствующих интегральных уравнений теории упругости осуществляется методом последовательных перемещений. Важной особенностью алгоритма является независимость сетки разбиения при варьировании граничной поверхности области.
При использовании МГИУ решение второй основной задачи теории упругости (на граничной области поверхности задана нагрузка) сводится к решению сингулярного интегрального уравнения:
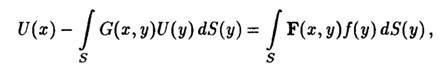(1.25) где S — граничная поверхность области; U — компоненты вектора перемещения на 5; G — ядро интегрального уравнения; F — матрица Кельвина- Сомильяна; f — компоненты вектора напряжений на S.
В [81] был разработан алгоритм решения уравнения (1.25) методом последовательных приближений с использованием регулярного представления сингулярного интеграла. При этом решение уравнения (1.25) представляется в виде ряда
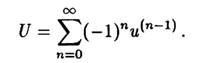(1-26)
Подставляя (1.26) в (1.25) и приравнивая коэффициенты при одинаковых степенях соответствующих членов ряда, можно получить рекуррентное соотношение для U:
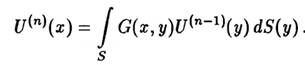(1.27)
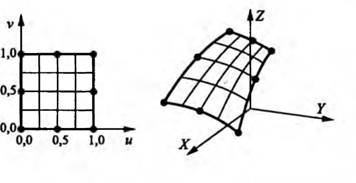
Рис. 1.19. Отображение криволинейного прямоугольника на единичный квадрат
Регулярное представление для входящего в (1.27) сингулярного интеграла получается путем понижения особенности с использованием обобщенной теоремы Гаусса. Тогда (1.27) приобретает вид:
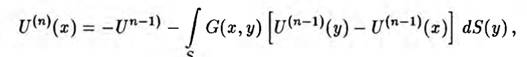(1.28) причем
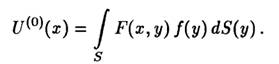(1.29)
После определения перемещений U напряжения на граничной поверхности S вычисляются путем численного дифференцирования перемещений и использования закона Гука. Так как для подавляющего большинства технических задач определяющим является напряженное состояние на границе области, этим, как правило, и завершается решение.
Описанный выше метод был реализован в виде универсального алгоритма [80, 82].
Характерной особенностью данного алгоритма является представление граничной поверхности в виде совокупности криволинейных четырехугольников. Такой способ аппроксимации граничной поверхности позволяет в значительной степени автоматизировать вычисление параметров дискретной модели. Каждый из криволинейных четырехугольников с помощью специальных функций формы отображается на единичный квадрат в криволинейных координатах и, υ (рис. 1.19).
Были использованы четырехугольники с восемью узлами и, соответственно, функции формы Сирендипова семейства второго порядка.
При этом отображение имеет вид:
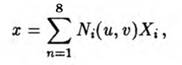(1.30) где х — текущая координата поверхности; и, ν — криволинейные координаты; Xi — координаты узловых точек; Ni — функции формы.
С использованием (1.30) и известных соотношений дифференциальной геометрии вычисляются все необходимые параметры расчетной сетки: координаты узлов дискретной модели, проекции вектора нормали к поверхности, площади элементов поверхности. Такой подход дает возможность в значительной степени автоматизировать подготовку исходных данных, так как все параметры дискретной модели в большей части генерируются программой.
Интерполяция плотности потенциалов осуществляется с помощью локальных сплайнов, а численное интегрирование на каждом из элементов расчетной сетки выполняется с использованием кубатурных формул, полученных путем перемножения соответствующих квадратур Гаусса. Выбор порядка формулы производится в зависимости от L/(X — Y), где L — максимальный линейный размер элемента, что обеспечивает для граничной поверхности в целом адаптивную кубатурную формулу.
При вычислении суммы ряда (1.26) учитывается, что данный ряд с увеличением п стремится к геометрической прогрессии, поэтому для уточнения суммы используется формула:
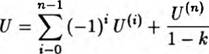
(1-31)
где к — приближенно определенный знаменатель прогрессии.
При этом дискретизация выполняется единообразно для каждого четырехугольника в криволинейных координатах, а затем полученная сетка отображается в декартовы координаты.
Современная версия программы, реализующая данный алгоритм, позволяет графическую интерпретацию результатов, реалистичное изображение объекта на дисплее компьютера и вывод изолиний напряжений. Она апробирована при расчете напряженно-деформированного состояния различных элементов энергетических, машиностроительных и других конструкций. Сравнение полученных результатов с экспериментальными данными и результатами, полученными другими численными методами, показало их хорошее совпадение.
Расчет гиба
В качестве расчетной принята схема толстостенной оболочки с заглушками по торцам (рис. 1.20). Рассмотрены два вида наиболее важных видов нагружения: внутреннее давление и распределенная по торцу нагрузка, передающая изгибающий момент от примыкающих участков паропровода. Это дало возможность при составлении расчетной схемы учесть симметрию геометрии и нагрузки и рассматривать только 1/4 часть области.
Сечение оболочки — эллиптическое кольцо, наружный и внутренний контуры которого смещены друг относительно друга по вертикальной оси.
С учетом симметрии геометрии и нагрузки граничная поверхность гиба аппроксимируется 26-ю криволинейными четырехугольниками. На рис. 1.21 показана схема разбиения граничной поверхности на криволинейные четырехугольники.
В пределах рассматриваемой постановки задачи форма гиба и действующие на него нагрузки однозначно определяются заданием следующих параметров:
DH — наружный диаметр, мм;
h — номинальная толщина стенки, мм;
R — радиус гиба, мм;
а — угол, рад;
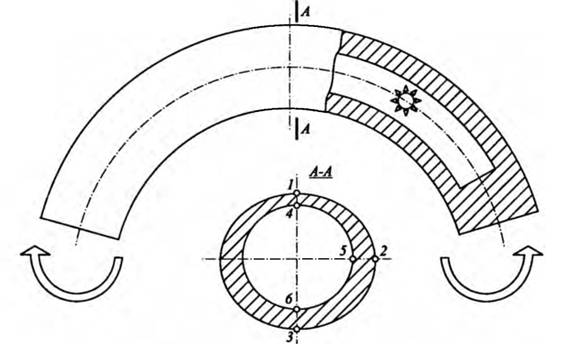
Рис. 1.20. Расчетная схема гиба
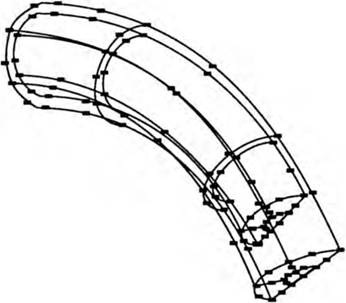
Рис. 1.21. Схема разбиения граничной поверхности гиба
а — овальность, %;
hmin, hmax — минимальная и максимальная толщина стенки, мм;
р — давление, МПа;
σmах ном — максимальное номинальное напряжение от действия момента, МПа.
Для упрощения подготовки исходных данных при варьировании параметров был разработан специальный пакет программ, автоматически генерирующий исходные данные для основной программы метода ГИУ по заданным значениям перечисленных выше параметров.
Для гиба со значениями параметров: DH = 159 мм; h = 18 мм; R = 600 мм; а = π/2; а = 6%; hmin = 14 мм; hmax — 18 мм; р — 20 МПа — были выполнены расчеты напряженного состояния (рис. 1.20, т. 1-6). При этом максимальные кольцевые напряжения составили 133 МПа, а такие же напряжения в растянутой образующей такого гиба, рассчитанные по методике [83], которая использует подход теории тонкостенных стержней, составили 140 МПа.
Расчет тройникового соединения
Конструктивные особенности тройников обуславливают возникновение значительной концентрации напряжений. Вместе с тем, сложность формы таких элементов значительно затрудняет расчет напряженного состояния в них. Применение простых расчетных моделей, полученных путем комбинации стержневых моделей сопротивления материалов, представляется необоснованным. Более сложные расчетные схемы, основанные на теории тонких упругих оболочек, с одной стороны, приводят к необходимости разработки сложных алгоритмов, а с другой — не позволяют избежать значительной погрешности расчета, особенно при определении напряжений в зонах концентрации и при расчетах толстостенных тройников.
В нормах расчета на прочность оборудования АЭС [78] приводятся формулы для коэффициентов концентрации напряжений в тройниках, построенные путем обработки результатов большого количества численных и физических экспериментов. Но применение этих формул ограничено определенными соотношениями геометрических размеров. Причем в случае приложения осевых и моментных нагрузок толстостенные тройники оказываются за рамками допустимых параметров, да и сам коэффициент концентрации в этом случае толкуется довольно условно, без учета величины радиуса скругления в зоне соединения штуцера с трубой.
Учитывая вышесказанное, представляется актуальной разработка методики расчета напряженного состояния тройникового соединения, основанной на решении трехмерной задачи теории упругости. Как и для гиба, в качестве метода решения такой задачи используется метод граничных интегральных уравнений.
Построение расчетной модели. Рассмотрены только неравнопроходные сварные тройники с перпендикулярным по отношению к трубе расположением штуцера. На рис. 1.22 представлена схема тройникового соединения. В качестве нагружающих факторов рассмотрены внутреннее давление и произвольно приложенные вектора сил и моментов к торцам трубы и штуцера, причем методически целесообразным представляется рассмотрение каждого фактора в отдельности. Таким образом, расчетная схема тройника однозначно определяется заданием следующих геометрических параметров:
DH, Dш — наружный диаметр трубы и штуцера;
h, hш — толщина трубы и штуцера; р — радиус скругления;
b, bш — длина трубы и штуцера, отнесенная к ее(его) диаметру;
Рис. 1.22. Схема тройникового соединения
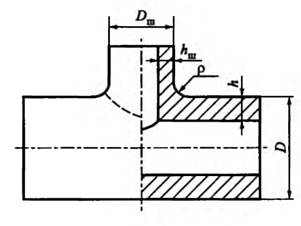
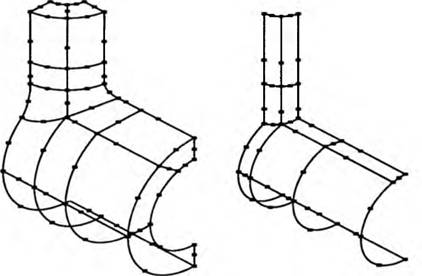
Рис. 1.23. Схема разбиения граничной поверхности тройника на криволинейные четырехугольники и одного из параметров нагружения: р — давление среды;
N, Nкр — осевое усилие, приложенное к трубе или штуцеру;
Mх изг, Мх изг. ш — изгибающий момент в плоскости тройника, приложенный к трубе или штуцеру;
Μz изг, Мх изг. ш — изгибающий момент из плоскости тройника, приложенный к трубе или штуцеру;
Мкр, Мкр. ш — крутящий момент, приложенный к трубе или штуцеру;
В соответствии с описанным выше алгоритмом, граничная поверхность аппроксимируется совокупностью криволинейных четырехугольников. Благодаря учету геометрической симметрии рассматриваемой конструкции тройника и симметрии нагрузки (в том числе и обратной), достаточно рассматривать соответствующую четвертую часть области. Разбиение наружной и внутренней граничной поверхности на криволинейные четырехугольники показано на рис. 1.23.
Используемая программа решения трехмерных задач теории упругости МГИУ позволила проводить так называемую «параметризацию», т. е. встраивать в программу специальные блоки, автоматически генерирующие исходные данные по значениям перечисленных выше основных параметров, определяющих геометрию тройника и нагрузку.
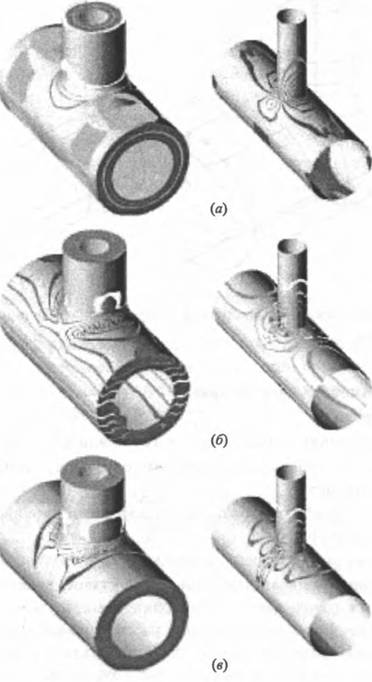
Рис. 1.24. Изолинии эквивалентных напряжений на наружной и внутренней поверхности тройника для трех случаев нагружения: (а) внутренним давлением; (б) изгибающим моментом; (в) осевым усилием
Сходимость МГИУ к соответствующему точному решению задачи теории упругости показана теоретически, но при решении конкретных задач необходимо рационально выбрать сетку дискретизации, обеспечивающую приемлемую точность решения без излишних затрат ресурсов компьютера.
Для оптимального выбора параметров дискретизации модели, показанной на рис. 1.23, для тройника, подверженного воздействию внутреннего давления, были выполнены расчеты при различных значениях параметра разбиения. Под этим параметром подразумевается число элементов, на которое разбивается каждый из криволинейных четырехугольников по каждой из криволинейных координат. При значении параметра разбиения п, равном 4, достигалась приемлемая сходимость. Отмечено также хорошее совпадение с результатами расчета по формулам [78].
Для иллюстрации характера распределения напряжений по граничной поверхности тройника на рис. 1.24 показаны линии равных напряжений (изостаты) для трех случаев нагружения: внутренним давлением (а), изгибающим моментом, приложенным к трубе и действующим в плоскости тройника (б), осевым усилием, приложенным по оси трубы (в). Изолинии построены для максимальных касательных напряжений, в соответствии с применяемой в нормативных документах теорией прочности для энергетических конструкций.
Выводы
- Современные методы расчета трубопроводных систем позволяют эффективно оценивать прочность элементов трубопроводов с учетом основных нагружающих факторов и реальной конфигурации трубопровода.
- Для наиболее ответственных элементов трубопроводов разработаны методики расчета на прочность, в том числе и уточненные, базирующиеся на современных численных методах механики сплошной среды.
- Разработаны и реализованы на современных компьютерах алгоритмы расчета трубопроводных систем и их элементов.
