Порядок и критерии расчета на прочность элементов трубопроводов ТЭС регламентируются нормами расчета на прочность [77]. Там же приведены и расчетные формулы для основных элементов трубопроводов. Ниже даны некоторые сведения о моделях и подходах к расчету прочности сложных конструктивных элементов трубопроводов — гибов и тройников.
Гибы
При эксплуатации паропроводов тепловых электрических станций в группу наиболее часто повреждаемого ответственного оборудования входят гнутые элементы паропроводов или, как их обычно называют, гибы. Это связано с конструктивными особенностями гиба и технологией его изготовления, обусловливающей местное утонение стенки, отклонение формы сечения от круговой и снижение прочностных свойств металла.
Существует целый ряд модификаций методов, основанных на технической теории тонких оболочек, для расчета на прочность гибов. Ниже приведена методика, предложенная Д. Л. Костовецким [76]. Основные положения этой методики нашли отражение и в современных нормативных документах.
Для определения максимального эквивалентного напряжения в колене, имеющего эллиптическую форму сечения, при воздействии внутреннего давления, изгибающего и крутящего моментов служат следующие формулы:
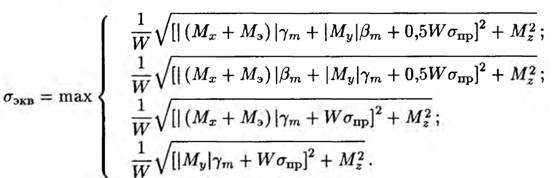(1-19)
Здесь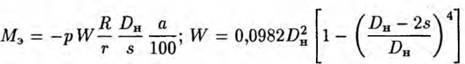
— момент
сопротивления поперечного сечения изгибу;
— приведенное напряжение в колене при действии одного давления; γт, βт — коэффициенты интенсификации тангенциальных (окружных) и продольных (осевых) напряжений изгиба, определяемые из специальных номограмм; Μz — крутящий момент; φ — коэффициент прочности; С — прибавка к расчетной толщине стенки; Мх, Му — соответствующие проекции вектора изгибающего момента; р — внутреннее давление; Dн — наружный диаметр трубы; s — толщина трубы; R — радиус гиба; r — средний радиус трубы; а — овальность.
Максимальное эквивалентное напряжение в колене при действии одного давления можно вычислить по формуле
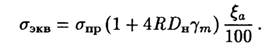(1-20)
Коэффициент ξα введен для учета отличия действительной формы искажения поперечного сечения от идеальной эллиптической. Среднее (наиболее вероятное) значение ξα при эллиптичности 5; 10; 15% составляет, соответственно, 1,6; 1,3; 1,2; максимально возможные значения ξο для тех же значений эллиптичности — 2,6; 1,8; 1,5.
Для колена высокотемпературного трубопровода формулу (1.19) следует применять с введением коэффициента χ3, учитывающего постепенное уменьшение изгибного напряжения вследствие накопления деформации ползучести,
(1-21)
Тройники
Ответственными элементами паропроводов тепловых электрических станций являются тройниковые соединения труб, или тройники. Сложность формы этих элементов затрудняет их расчет на прочность. Ниже приведена упрощенная инженерная методика такого расчета [78].
Для тройникового узла напряжения вычисляют в трех сечениях — месте примыкания штуцера к трубе (в двух сечениях) и посредине штуцера.
Для места примыкания штуцера к трубе напряжения определяются по формулам:
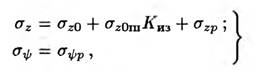(1.22) где
— суммарный изгибающий момент, приложенный к трубе; N — осевое усилие, приложенное к трубе; W — момент сопротивления сечения трубы; s — площадь сечения трубы; Киз — коэффициент местных напряжений (изгиба):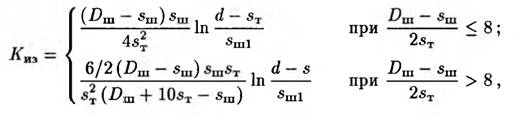 
где Dш, sш — наружный диаметр и толщина штуцера; σz — осевое напряжение; σψ — кольцевое напряжение.
Если Киз < 2, то следует принимать Киз = 2.
В середине штуцера напряжения определяются по формулам:
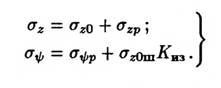(1-23)
Помимо указанных сечений, проверка прочности выполняется и в точке на кромке пересечения внутренних поверхностей трубы и штуцера, где имеет место концентрация кольцевых напряжений. Остальные компоненты тензора напряжений для этой точки вычисляются как для места примыкания штуцера к трубе:
(1-24) где
— коэффициент концентрации тангенциальных напряжений на кромке отверстия; d = D — 2sT.
После вычисления компонент тензора напряжений проверка прочности выполняется с использованием теории наибольших касательных напряжений.
