8.6.6. Оптимальный синтез солнечно-теплонасосных систем с сезонным аккумулированием на графе термоэкономических затрат
Описанный в предыдущем параграфе алгоритм ΑΖ дает возможность определять термоэкономические характеристики СТНССА на основе соответствующего эксергетического потокового графа Е = (А, Г) и тем самым вести их эволюционную оптимизацию на основе сопоставительного анализа различных СТНССА.
Однако, базируясь на специфике СТНССА, а именно на том, что эти системы легко трансформируются в однонаправленные или линейные, мы предлагаем иную модель, позволяющую строить более эффективные процедуры оптимизации СТНССА [27].
Вначале рассмотрим однородную СТНССА, состоящую из различных элементов, в которой один поток hx последовательно и однократно взаимодействует с п потоками (рис. 8.4).
![]()
Рис. 8.4. Линейная система СТНССА
В этом случае задача оптимального синтеза может быть сформулирована следующим образом: требуется так распределить множество потоков С.,, i = 1, 2, п вдоль потока /г., j = 1, чтобы параметры потока h после системы находились в заданном интервале значений, а выбранный критерий оптимальности имел минимальное значение.
В качестве критерия оптимальности примем суммарные термоэкономические затраты в СТНССА:



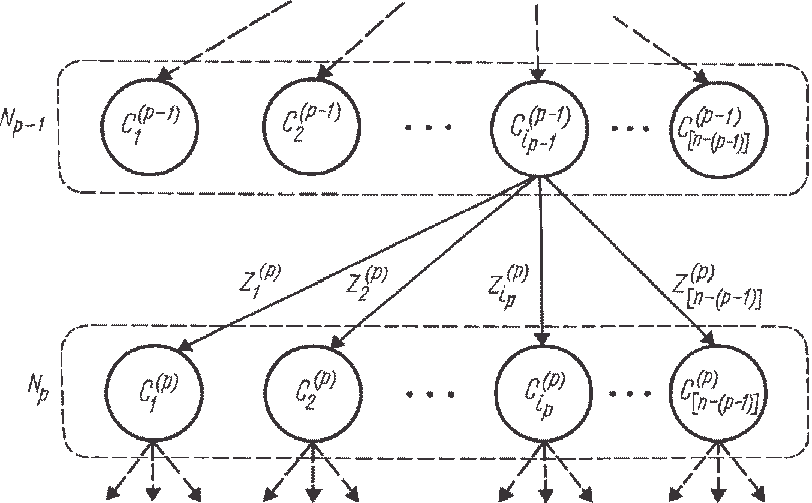
Рис. 8.5. р-й и (р — 1)-й уровни графа эксергоэкономических затрат в линейной системе СТНССА

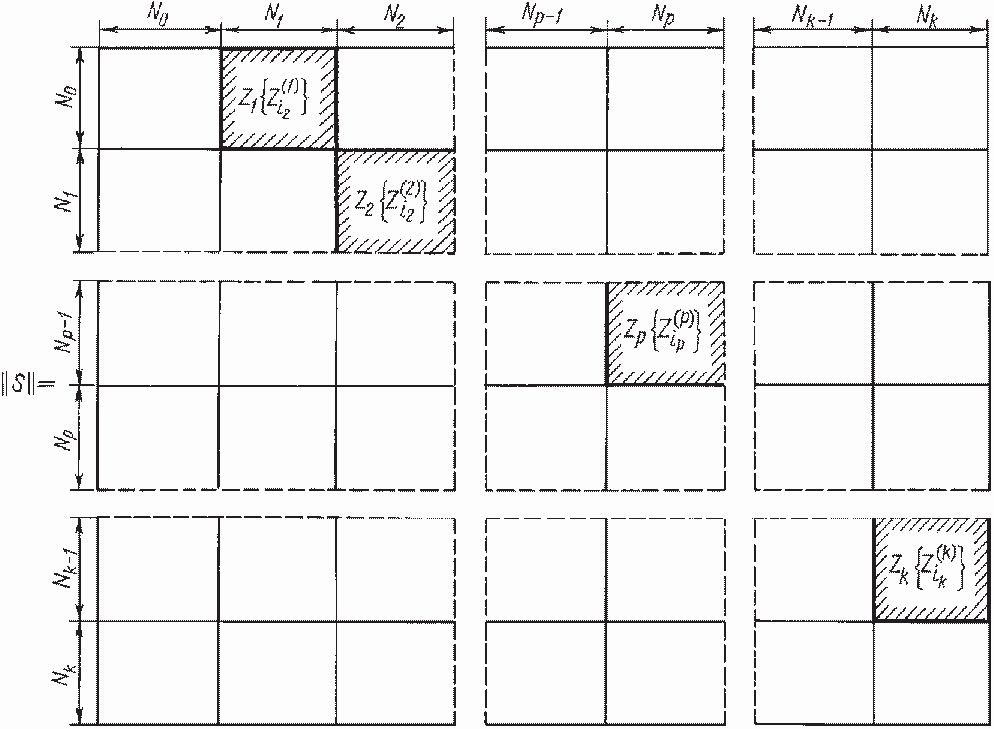
Рис. 8.6. Матрица возможных значений эксергоэкономических затрат в линейной СТНССА
Так как алгоритм Веллмана—Калаба ведет поиск оптимального варианта по всем элементам матрицы на рис. 8.6, а не только по заштрихованным, то его непосредственное применение нерационально из-за необходимости анализа большого числа «лишних» вариантов. При использовании рассмотренных особенностей графа термоэкономических затрат мы разработали более простой алгоритм поиска оптимального варианта на основе метода динамического программирования, позволяющий уменьшить число итераций в п раз.



