4.4.3. Процессы перемешивания субстрата в реакторе биогазовой установки
Перемешивание механическими мешалками
Процессы перемешивания в жидких средах при помощи механических мешалок широко распространены во многих отраслях техники, например для приготовления суспензий и аэрозолей в сельском хозяйстве. Перемешивание с использованием механических мешалок гомогенизирует гетерогенные системы и интенсифицирует технологию использования полученных двухфазных сред [76]. Результаты исследований по изучению влияния процесса перемешивания на количество выделяемого биогаза приведены на рис. 4.11 [77]. Можно заметить, что выход метана увеличивается почти в 1,5 раза.
В основе процессов перемешивания лежат гидродинамические явления, возникающие при вращении среды в соответствующем аппарате. Для исследования этих процессов следует обратиться к методам математического и физического моделирования.
Структура потока в аппарате в процессе перемешивания описывается дифференциальными уравнениями движения жидкости.
Авторы работы [78] предложили разбить весь объем, где происходит перемешивание, на шесть зон:
- поток от мешалки, который моделируется как тангенциальный поток;
- поток от мешалки, направляющийся к внутренней поверхности стенки аппарата. Этот поток рассматривается как застойная зона, поскольку он ударяется о стенку и скорость его равняется нулю;

- поток в верхних и нижних углах аппарата, который моделируется как потенциальный поток;
Рис. 4.11. Динамика выхода метана при анаэробном сбраживании навоза крупного рогатого скота (40 %):
1 — в стационарном режиме; 2 — при перемешивании
- поток у стен аппарата (в верхней, нижней и средней частях этого участка течения), который рассматривается как потенциальный поток;
- поток у оси в центре аппарата, который соответствует представлению о циркуляционном потоке;
- кольцевой поток, который моделируется как застойная зона.
Структура потока в аппарате симметрична относительно оси мешалки.
Предлагаемая модель потока в объеме аппарата является условной, но она в достаточной степени отражает физику процессов при перемешивании.
Рассмотрим математические модели изложенных выше потоков течения.
Тангенциальный поток от мешалки является осесимметричным и описывается системой уравнений

Предположим, что тангенциальный поток одномерный. В этом случае для профиля скорости в направлениях следуют соотношения
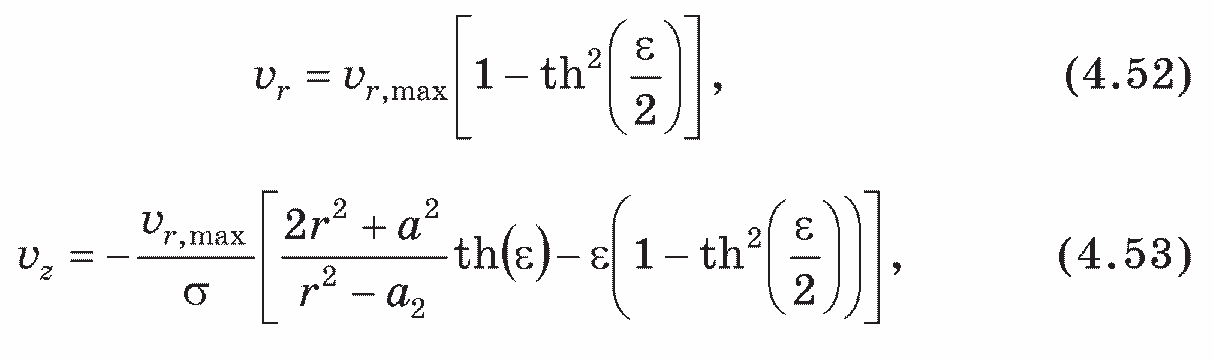


Результаты расчета по приведенным выше уравнениям для конкретного аппарата позволяют получить только качественную картину течения, но не количественные данные.
В гладкостенных аппаратах перемешивание сопровождается образованием центральной воронки. Глубина и форма воронки характеризуют эффективность технологии перемешивания. Этому вопросу посвящен ряд исследований. Результаты экспериментальных данных, как правило, представлены в виде критериальных зависимостей.
Для радиально-лопастных мешалок предложена расчетная формула, по которой определяют глубину воронки [79]

Представляют несомненный интерес расчетные выражения, предложенные в работах [80, 81].
Для исследования процессов перемешивания рекомендуется пользоваться математическими моделями, основанными на принципах гидродинамики жидкости. При этом, надо иметь в виду, что поток характеризуется неравномерностью, а время пребывания частиц в реакционном объеме не одинаково в силу стохастической природы их движения. Причинами неравномерности структуры потока в аппарате в процессе перемешивания являются: неравномерности профиля скоростей; турбулизация потока; молекулярная диффузия; явления
байпасирования, проскока и застойных зон. В гладкостенных аппаратах на поверхности стенки образуется пограничный слой, сопровождаемый отрывными явлениями и вихреобразованиями.
Поэтому в первом приближении рекомендуется исходить из модели идеального смешивания, которая является моделью макросмешивания. При этом не учитываются локальные, более мелкие явления. Такая модель, в частности, особенно целесообразна при отсутствии механического перемешивания, когда энергия входного потока расходуется на образование конвективных токов и турбулентных вихрей, которые и вызывают перемешивание жидкости в аппарате. В этих случаях для описания протекающих в аппарате физических явлений следует обратиться к уравнениям Навье—Стокса и можно не принимать во внимание ускорение поля внешних массовых сил, а также перепад давления в объеме жидкости, так как они пренебрежимо малы по сравнению с инерционными силами и силами трения. В результате уравнение движения имеет вид [82]

Для процесса перемешивания имеет значение энергия, расходуемая на преодоление сил вязкого трения, которая определяется из выражения

Уравнение (4.65) после ряда простых преобразований приводится к безразмерному виду
![]()
(4.68)
Тщательно проведенные исследования [83] показали, что режим идеальной жидкости применим при Re > 13,5.
Если перемешивание не подчиняется законам движения жидкости, необходимо обратиться к другим моделям для их описания. В процессах неидеального смешения наблюдаются диффузионные явления. В этом случае математическая модель в безразмерном виде есть связь между числами Пекле и Рейнольдса
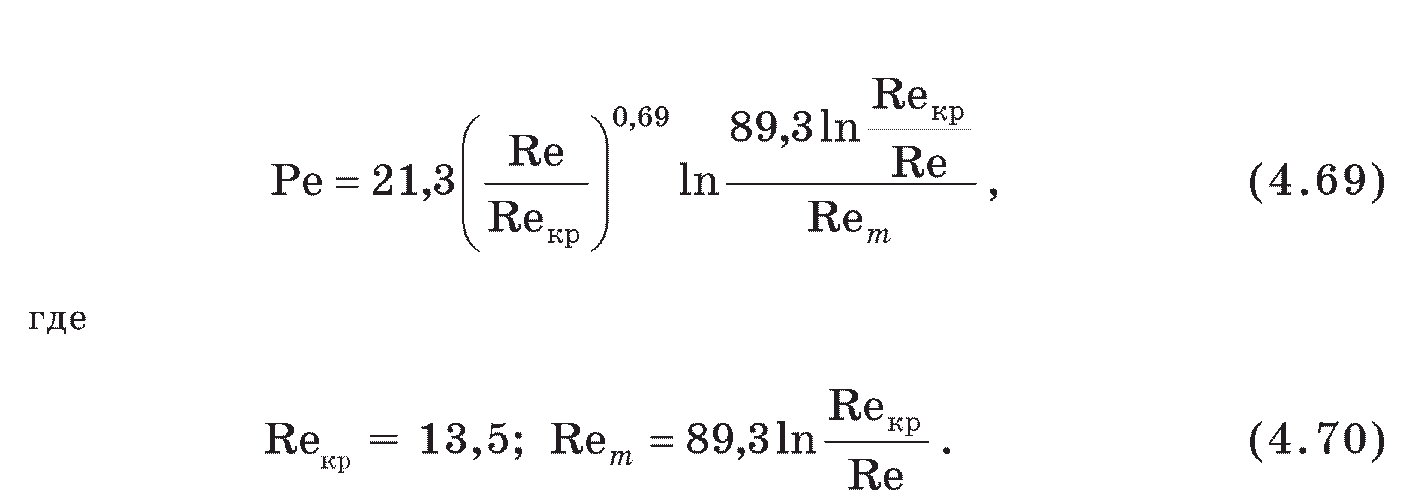
Гидродинамика перемешивания гетерогенных сред.
Часто мы встречаемся с гетерогенными средами. Анализу движения твердой частицы, взвешенной в турбулентном потоке, посвящено значительное количество работ. Среди них надо выделить монографии С. Соу, О. Хинце, Р.И. Нигматулина, Р. Бусройда, Г. Уоллиса [84-90].
Приведем систему уравнений, описывающую течение гетерогенной среды. При этом принято отдельно писать уравнения для каждого компонента смеси.
Обозначим объемную долю частиц взвеси через а. В этом случае уравнение неразрывности для жидкой фазы имеет вид

Прежде чем записать уравнения движения, определим скорость потока
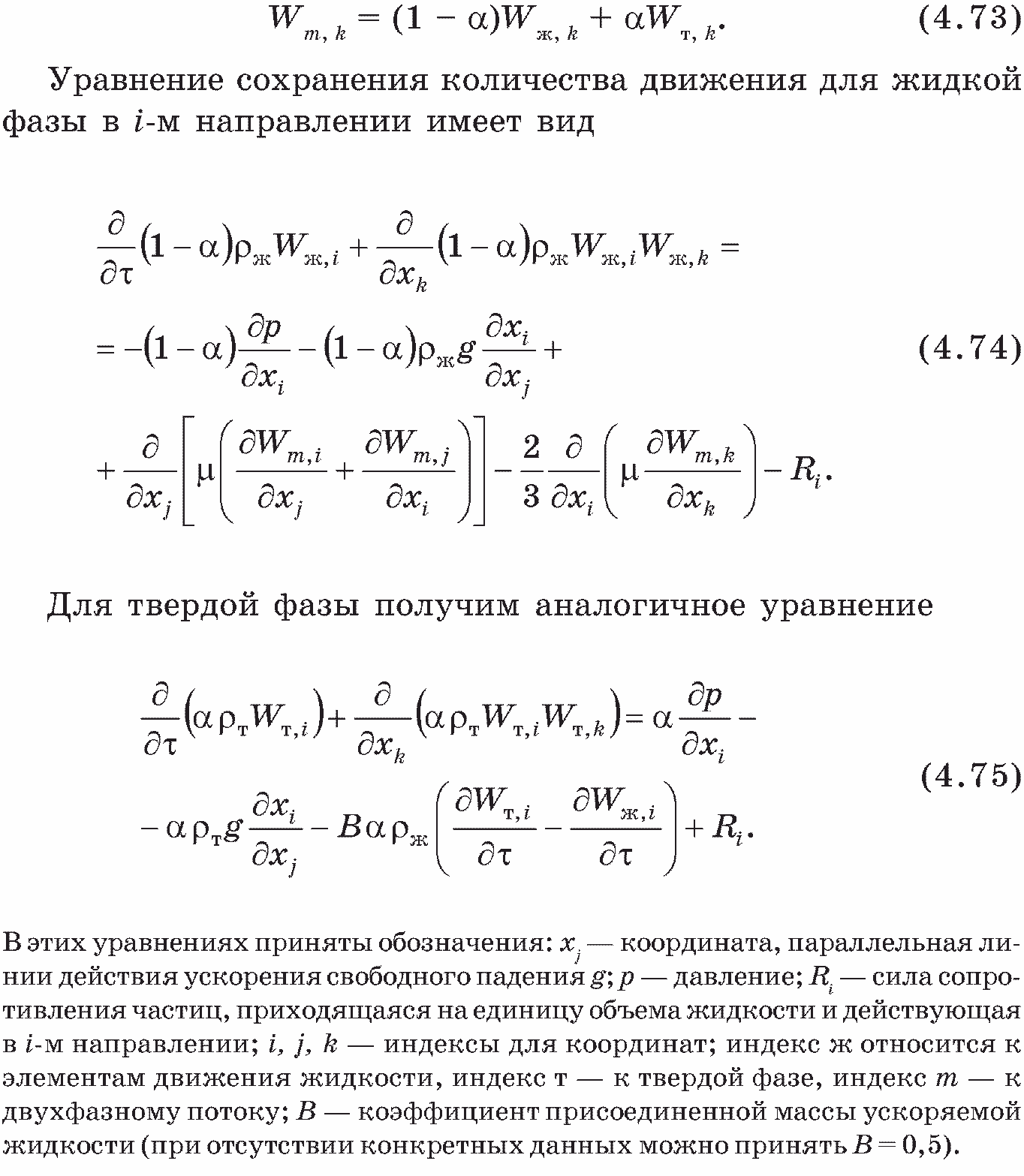
Для турбулентного потока взвеси необходимо учитывать турбулентные пульсации скорости, тогда уравнения движения имеют более сложный вид.
Проблема расхода энергии имеет немаловажное значение, и этому посвящено значительное количество работ. В этих работах исследовано влияние на мощность, потребляемую при перемешивании, геометрических параметров мешалки и аппарата [85-87], критериев Рейнольдса и Фруда в различных режимах перемешивания: ламинарном, переходном, турбулентном. Исследования показали, что для мешалок различного типа в аппаратах с отражательными перегородками и в гладкостенных аппаратах мощность, затраченная на перемешивание, не зависит от критерия Фруда при значении Re < ReKp. Критическим число Рейнольдса ReKp будет тогда, когда возникает воздушная прослойка, которая достигает лопастей мешалки, и она содействует аэрации жидкости.
При перемешивании гомогенных жидкостей потребляемая мешалками мощность зависит от параметров жидкости, скорости вращения мешалки. На основе теории подобия и размерности получена следующая расчетная формула [91]

Формулой (4.76) трудно пользоваться для решения конкретной задачи, однако ее преимущество в том, что она указывает на степень влияния различных факторов на значение мощности Ν, дает качественную характеристику процесса перемешивания гомогенной смеси.
Для геометрически подобных аппаратов можно пренебречь последними девятью членами уравнения, тогда

При установлении в процессе перемешивания турбулентного режима мощность, потребляемая мешалкой, не зависит от вязкости перемешиваемой среды, а определяется плотностью последней. На энергию, расходуемую мешалкой, влияют, кроме того, частота вращения и диаметр мешалки. Для лопастных и турбулентных мешалок предложена расчетная зависимость [91, 92]

Мощность, потребляемая при перемешивании скребковыми мешалками, определяется как сумма трех составляющих в зависимости от зоны аппарата [94]: у вала мешалки; у внутренних стенок аппарата; между лопастью мешалки и стенкой аппарата.
На основе многочисленных опытов получено следующее выражение для критерия мощности:

![]()
Первый член в уравнении (4.80) учитывает потери энергии в зоне между лопастью мешалки и стенкой аппарата, второй — расход энергии у вала мешалки, третий — у внутренних стенок аппарата.
Более простая расчетная формула предложена авторами работы [94]
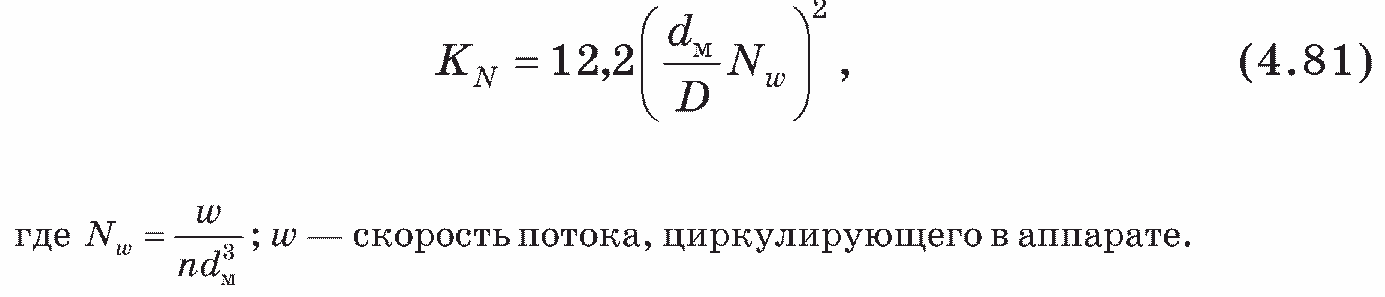
Рассмотрим аппарат с перемешиванием двухфазной системы, которая подогревается электронагревателем (рис. 4.12).
Для анализа процесса перемешивания в таком аппарате используем теорию графов. Построим структурный граф (рис. 4.13) и сигнальный граф (рис. 4.14) для приведенной установки.
На схемах приняты обозначения: Qn — теплота, вводимая электронагревателем; Qo — теплота, поступающая в теплообменник с субстратом; — потери теплоты из реактора в окружающую среду; Q2 — теплота, удаляемая из реактора со шламом.

Рис. 4.12. Подогрев суспензии в аппарате перемешивания

Рис. 4.13. Структурный граф теплообмена в аппарате перемешивания
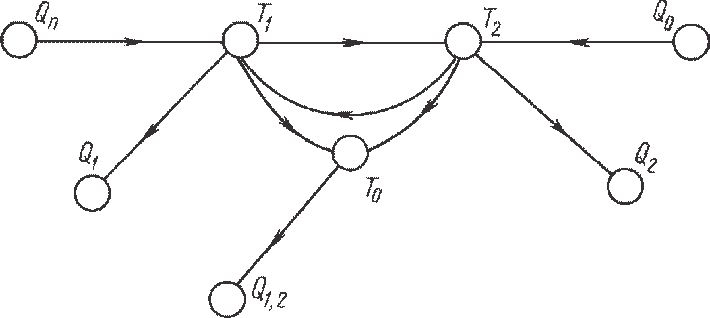
Рис. 4.14. Сигнальный граф теплообменника
Приведенные графовые построения могут использоваться для термоэкономической оптимизации показанной на рис. 4.12 установки.
В качестве перемешивающего устройства можно использовать барботер с рециркуляцией биогаза. В работе [95] приведена методика расчета барботера установки метанового сбраживания птичьего помета.

