Оптимизация с-х энергетических установок - Термогидродинамические процессы в геотермальных системах

Рассмотрим отдельно математические модели для геотермальных скважин разной структуры.
В настоящее время используются всевозможные методы и методики, созданные на основе численного или аналитического решения задач теплопереноса в гетерогенных средах. К сожалению, эти методы и методики представлены в основном либо в виде авторских компьютерных программ, либо в виде сложных аналитических решений, что затрудняет непосредственное применение их в практике инженерных гидрогеологических расчетов. В связи с этим целью настоящего исследования является получение на базе уже существующих математических моделей и их аналитических решений простых инженерных формул и компьютерных программ для вычисления следующих технологических параметров, используемых при оценке восполняемых ресурсов (запасов) гидротерм или разработке проектов гидротермальных месторождений. Кроме того, в задачу входило составление пакета компьютерных программ, позволяющих рассчитать изменение во времени температуры теплоносителя как в разрабатываемом коллекторе, так и на устье эксплуатационных скважин.
Прежде чем перейти к описанию формул, рекомендуемых для определения перечисленных технологических параметров, охарактеризуем используемые математические модели и полученные на их основе аналитические решения.
Рассмотрим процесс теплопереноса, происходящий в подземном геотермальном коллекторе, схема которого показана на рис. 7.3. Для математического описания рассматриваемого процесса можно использовать следующие четыре известные расчетные схемы [6-9].

1. Упрощенная схема чисто конвективного теплопереноса в гомогенном теплоизолированном проницаемом пласте. Она подробно описана в работе [9] и сводит процесс теплопереноса в реальном подземном коллекторе к процессу конвективного теплопереноса в условно однородной проницаемой среде с так называемыми эффективными параметрами: эффективной теплоемкостью сэ и эффективной плотностью рэ. Математически рассматриваемая схема выражается уравнением

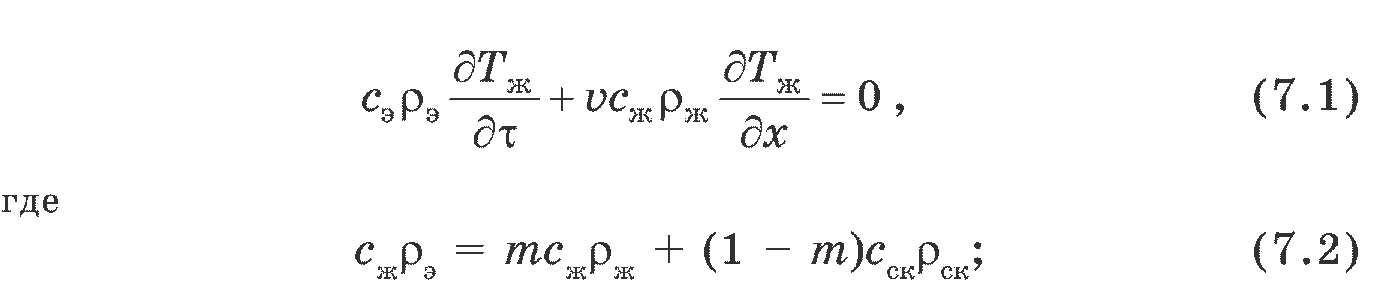
Тг — условно средняя температура фильтрующейся жидкости; τ — время; х — пространственная координата; υ — средняя скорость фильтрации; сж, рж, Сск» Рек — удельные теплоемкости и плотности соответственно жидкости и скелета пород; т — пористость.

Рис. 7.3. Схема теплопереноса в геотермальном коллекторе

1. Упрощенная схема кондуктивно-конвективного теплопереноса в гомогенном теплоизолированном проницаемом пласте. Она подробно описана в работе [9] и сводит процесс теплопереноса в реальном подземном коллекторе к процессу кондуктивно-конвективного теплопереноса в условно однородной проницаемой среде с эффективными параметрами, Причем в этой схеме кроме эффективной теплоемкости и плотности используется еще и эффективная теплопроводность λ . Математически рассматриваемая схема выражается уравнением

1. Схема конвективного теплопереноса в гомогенном проницаемом пласте с учетом теплопритока от окружающего массива непроницаемых пород. Она подробно описана в работах [6, 9, 10] и сводит процесс теплопереноса в реальном коллекторе к процессу конвективного теплопереноса в однородном пласте, имеющем эффективные параметры с учетом теплопритока от окружающего массива. Разновидность рассматриваемой схемы, в которой вместо эффективных параметров пласта используются теплофизические свойства жидкости, известна в литературе как схема Ловерье [10]. Математически эта схема выражается системой уравнений

(7.5)

Приведем точные аналитические решения описанных выше математических моделей теплопереноса в подземном геотермальном коллекторе. Для этого рассмотрим упрощенную схему чисто конвективного теплопереноса в гомогенном теплоизолированном пласте.

Уравнение (7.12) представляет собой линейное однородное дифференциальное уравнение в частных производных первого порядка. Характеристическое уравнение, соответствующее этому дифференциальному уравнению, имеет вид [11, 12]

Подставив производные (7.19) и (7.21) в исходное уравнение (7.12), получим запись рассматриваемой задачи в новой системе координат

(7.22)

После преобразований имеем

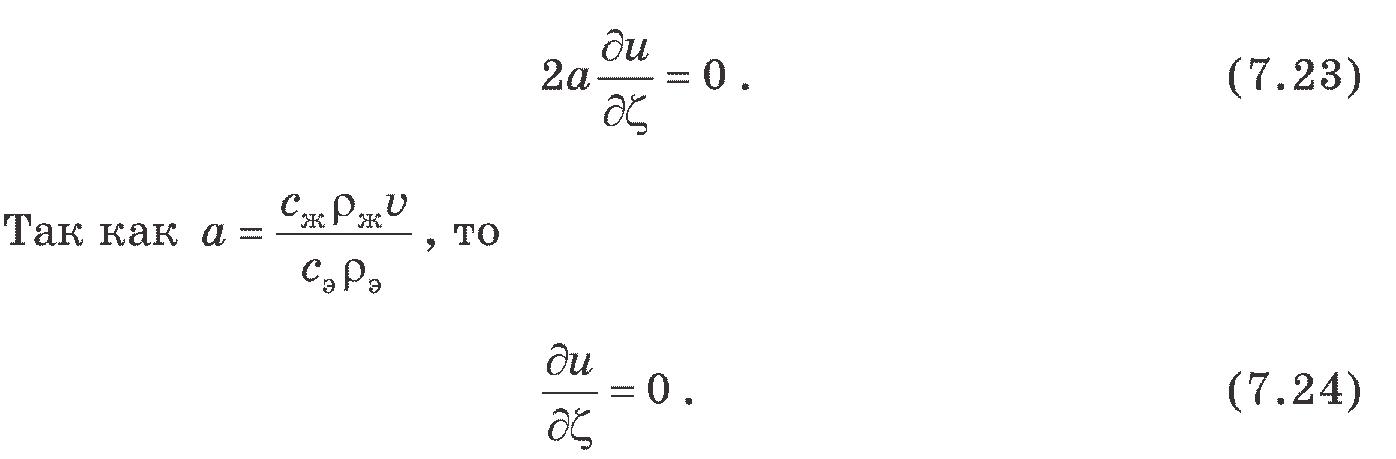
Тогда решение уравнения (7.24) имеет вид

(7.25)
Подчеркнем, что и является произвольной непрерывной дифференцируемой функцией, описывавшей множество решений уравнения (7.12). Конкретный вид этой функции, являющейся решением уравнения (7.12) при краевых условиях

1. , (7.15), получаем подстановкой в (7.26) выражений
2. и (7.15)

и применив обратное преобразование Лапласа по s, получим решение рассматриваемой краевой задачи при граничных условиях (7.32) и (7.33)

(7.45)

Решение же рассматриваемой краевой задачи при граничных и начальных условиях (7.30), (7.31) имеет вид

(7.46)
где Θ — безразмерная температура.

Окончательно решение уравнения (7.3) при краевых условиях (7.30) и (7.31) с учетом (7.46), (7.49), (7.34) имеет вид

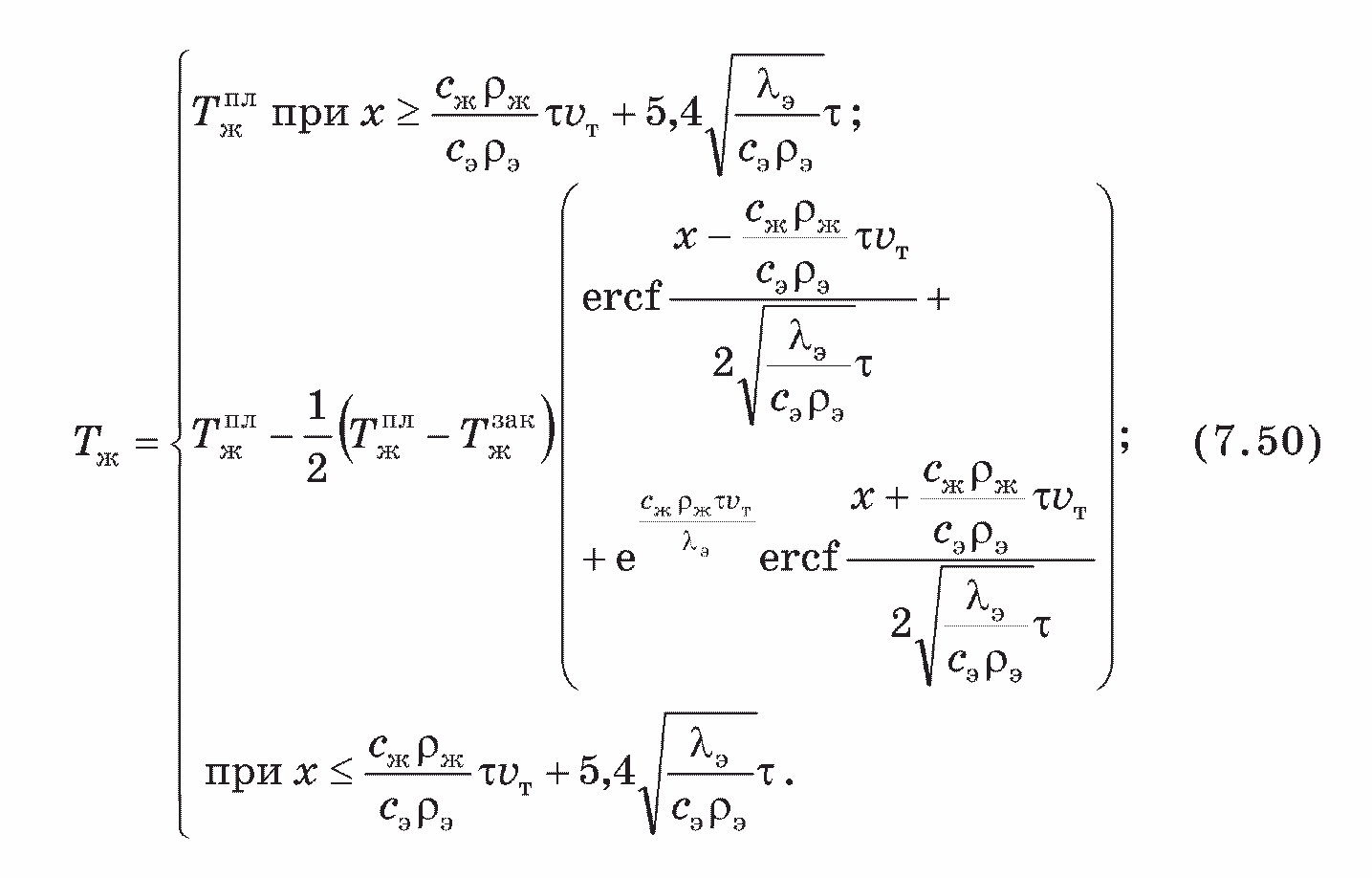
Рассмотрим схему конвективного теплопереноса в гомогенном проницаемом коллекторе с учетом теплопритока от окружающего массива.
Решим уравнения (7.5), (7.6) при следующих краевых условиях:
начальные условия

399

Для решения задачи (7.59)-(7.61) применим метод преобразований Лапласа [10-13]

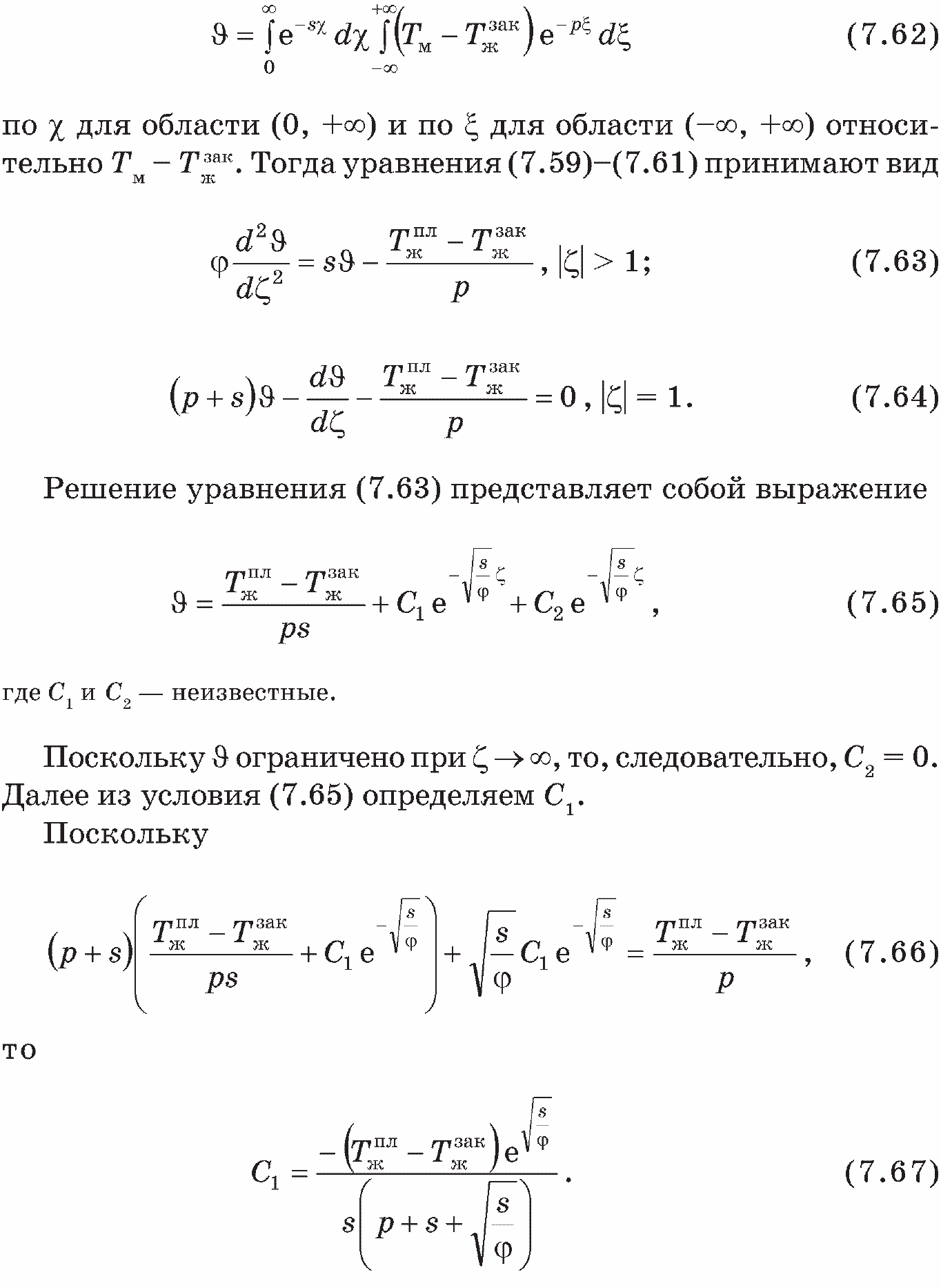
Следовательно, решение задачи (7.63)-(7.64)

(7.68)

Используя известные формулы операционного исчисления [11-13]

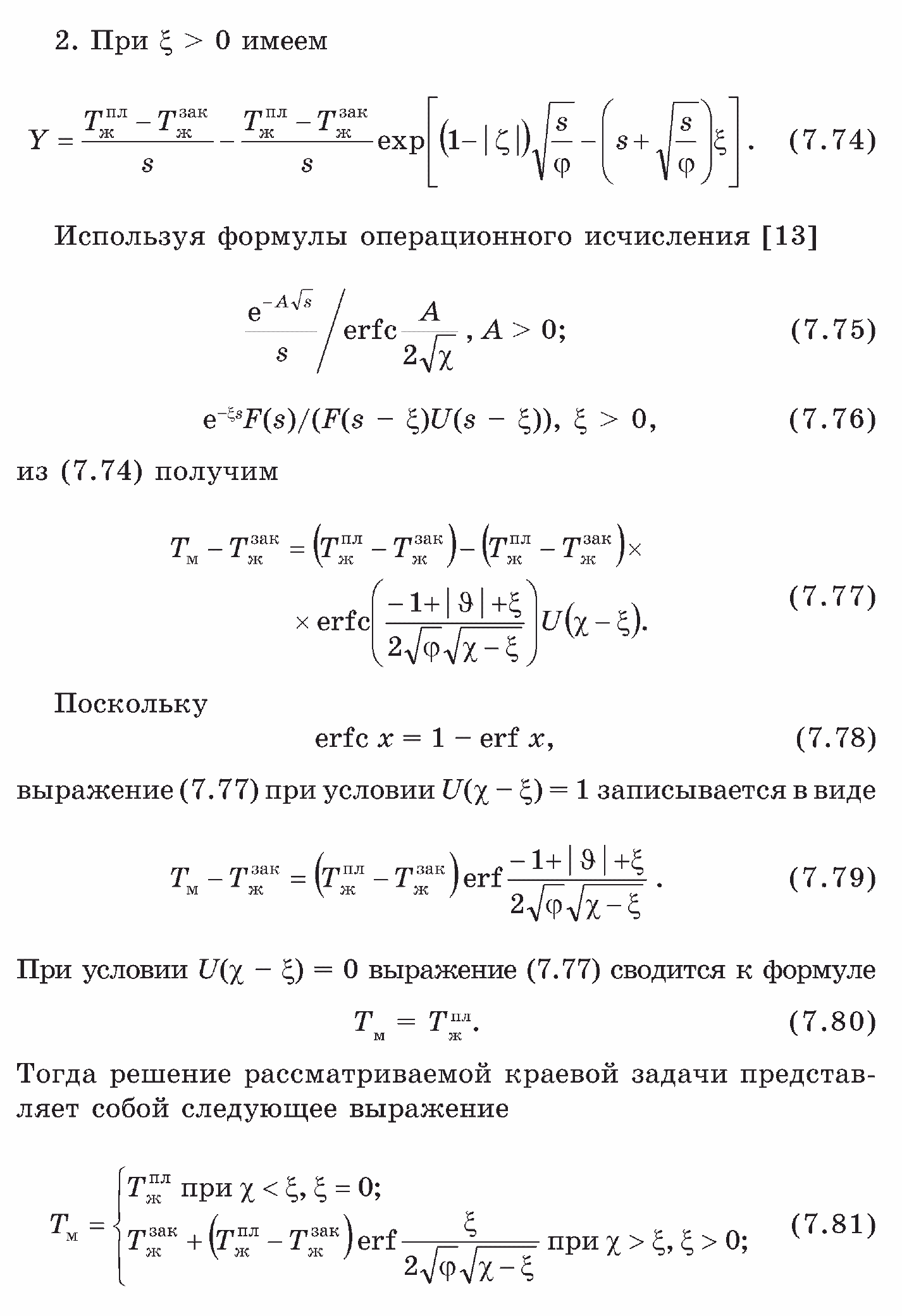
Подставляя в формулы (7.81), (7.82) выражения для безразмерных величин (7.57), получим решение уравнений (7.5), (7.6) при краевых условиях (7.51)-(7.55)

Рассмотренные математические модели и полученные на их основе аналитические решения позволяют с определенной степенью достоверности рассчитать:
расстояние между контуром отбора гидротерм и контуром нагнетания отработанного теплоносителя;
период добычи геотермального флюида постоянной пластовой температуры из продуктивного коллектора, в пределах которого организована закачка охлажденных вод.
Зависимости для вычисления расстояния между контуром отбора и контуром нагнетания теплоносителя получаются на основании решений (7.29), (7.50) и (7.83) и имеют вид:
схема гомогенного пласта (зависимость (7.29))

(7.85)
схема гомогенного пласта с учетом кондукции (зависимость (7.50))

(7.86)

схема гомогенного пласта с учетом теплопритока (зависимость (7.83))

(7.87)
В зависимостях (7.85)-(7.87) L — расстояние между контуром отбора и нагнетания; τ б — период разработки геотермального месторождения или период, на который подсчитываются восполняемые запасы термальных вод. Остальные обозначения прежние.
Зависимости для вычисления периода добычи геотермального флюида с постоянной температурой из продуктивного коллектора, в пределах которого организована закачка охлажденных вод, получены также на основании решений (7.29); (7.50) и (7.83) и имеют вид: схема гомогенного пласта

(7.88)
схема гомогенного пласта с учетом кондукции

схема гомогенного пласта с учетом теплопритока

(7.90)
Следует подчеркнуть, что входящая в зависимости (7.85)- (7.90) скорость фильтрации ν является средней скоростью фильтрации по кратчайшей линии тока между источником и стоком. Для радиальной фильтрации и при равенстве расходов и радиусов источника и стока эта скорость определяется по зависимости

где Q — расход источника стока; b — мощность пласта; г — радиус источника и стока; L — расстояние между источником и стоком.

Кроме расчетов перечисленных ранее технологических показателей с помощью приведенных решений (7.50) и (7.83) можно построить прогнозный график изменения во времени температуры геотермального флюида на устье эксплуатационной скважины, работающей во взаимодействии с нагнетательными скважинами. Для построения этого графика по зависимостям (7.50) и (7.83) на различные моменты времени вычисляется температура геотермального флюида. При этом значение координаты χ принимается постоянным и равным расстоянию между эксплуатационной и нагнетательной скважинами. Используя вычисленные на различные моменты времени значения температуры, строится требуемый прогнозный график.
Таким образом, в результате выполненной работы получены формулы для вычисления периода добычи геотермального флюида с постоянной температурой на устье эксплуатационной скважины, а также формулы для вычисления расстояний между контурами отбора и нагнетания системы геотермального месторождения [14].
Для описания неизотермической фильтрации по закону Дарси в геотермальных коллекторах блочного типа можно с незначительными упрощениями исходить из уравнений, приведенных в работах [15, 16]

Многими авторами [17-19] принимается, что в подземных геотермальных коллекторах коэффициенты теплоотдачи от твердого скелета к фильтрующейся жидкости бесконечно велики, поэтому температуры их выравниваются мгновенно.
Для коллекторов гранулярного типа рассматриваются физические модели, представляющие собой укладку сферических частиц [20-22]. Такая модель не слишком искажает результаты расчетов, но значительно упрощает решение задачи. Однако при этом нередко исходят из предпосылки, что число Рейнольдса имеет довольно высокое значение (Re > 10). Между тем фильтрация по закону Дарси происходит при Re < 1,0. При таких режимах движения коэффициент теплообмена мало зависит от скорости движения жидкости. Экспериментальные и теоретические исследования показывают, что для значительных гранулярных частиц (d4 >100 мм) при их омывании фильтрационным потоком коэффициенты теплообмена малы. Лишь при размерах частицы менее 10 мм коэффициенты теплообмена заметно возрастают.
Исследования показывают, что для коллекторов блочного типа передача теплоты велика, поэтому можно принять гипотезу мгновенного выравнивания температуры поверхности блоков и фильтрационного потока, которой придерживаются многие исследователи [17-20].
В последнее время появляется дополнительные исследования процессов тепломассообмена в геотермальных системах.
Конвективные потоки, возникающие в водоносном слое, зависят от многих факторов. В работе [23] приведены результаты исследований, отражающие зависимость конвективных потоков от пористости т и проницаемости k пласта. Установлено, что число Рэлея зависит от параметра m/k. Для специального режима с увеличением параметра m/k число Ra возрастает. Для неустановившегося режима течения, что характерно для условия аккумулирования теплоты, критическое значение Ra при m/k < 10 определяется зависимостью
(7.103)
Для значений 10 < m/k < 103 зависимость между Ra и m/k нелинейная [23]. Эти результаты совпадают с данными исследования, приведенными в работах [24, 25].
Представляют интерес исследования, приведенные в работе [26]. Численными методами анализа установлено, что при протекании жидкости вдоль вертикальной пористой среды наблюдаются отклонения от закона Дарси. Это вызнано отсутствием на отдельных участках течения проскальзывания на границе, а также инерционным эффектами. Подобное нарушение закона Дарси приводит к уменьшению потерь на трение, а также теплоотдачи, в то время как неоднородная пористость увеличивает теплоотдачу. При высоких числах Грасгофа эффекты инерции и дисперсии особо
ощутимы. Влияние поперечной тепловой дисперсии сводится к увеличению теплоотдачи. Силы инерции содействуют уменьшению теплоотдачи. Влияние этих двух факторов усиливается с увеличением неоднородности среды.
Проблема теплообмена в пористой геотермальной среде детально анализируются в работах [27, 28].
Изучение процесса стационарной свободной конвекции в вертикальной пористой среде показало, что в качестве определяющих параметров следует принимать число Рэлея, число Дарси и параметр диффузииа также отношение сторон канала H/L, где Л — отношение коэффициентов динамической вязкости жидкости в начале и в конце конвективного переноса; Н — высота, L — длина.
Исследования показали, что значительное влияние на поля скорости и температур в скважине оказывает число Дарси Da = fe/L2, где k — проницаемость. С увеличением числа Дарси, особенно при Da > 105, уменьшаются градиенты температур около стенок скважины. Уменьшаются также как локальное, так и среднее число Нуссельта, притом тем сильнее, чем выше значение числа Рэлея [29, 30].
Одним из эффективных средств исследования процессов тепломассообмена в водоносном аккумуляторе является метод физического моделирования, имитирующий геотермический энергетический контур. На основе физического моделирования процессов, протекающих в двух скважинах (дуплетная схема) [23], получены закономерности распределения температур в ней, в зависимости от расхода и температуры нагнетаемой воды. На основе этих исследований определено совместное влияние вынужденной и свободной конвекций на процесс теплообмена в насыщенной жидкостью пористой среде.
Математическую модель термогидродинамических процессов при движении пара в скважине можно составить, используя выражение первого закона термодинамики для потока и известные соотношения для коэффициента гидравлических потерь.

Исходя из первого закона термодинамики уравнение энергии для установившегося потока теплоносителя в вертикальной скважине геотермальной системы можно записать следующим образом [32]

Коэффициент гидравлических потерь, как известно, зависит от режима движения и характеристики канала. Для течений, характеризующихся числами Рейнольдса

Зависимость между термодинамическими параметрами, как известно, выражается уравнением состояния. Для перегретого, насыщенного и влажного водяного пара уравнения состояния имеют разный вид.
Для насыщенного пара зависимость давления от температуры определяется формулой Клапейрона—Клаузиуса

При низких давлениях применяется приближенная зависимость

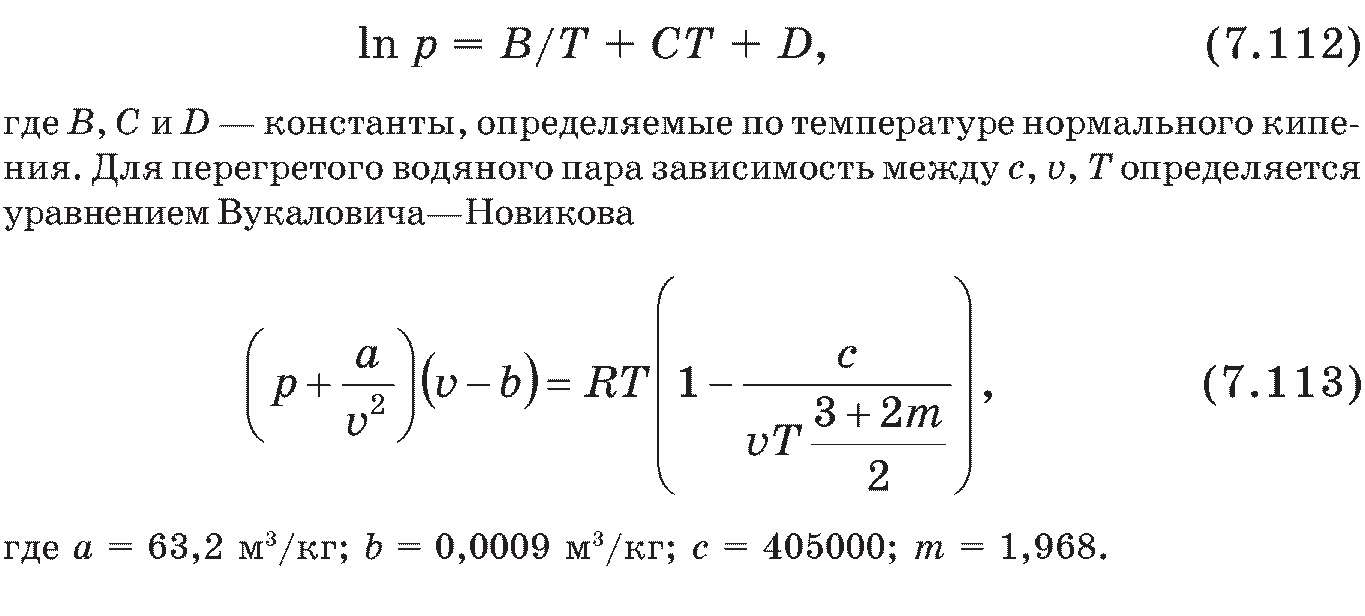
В качестве приближенного уравнения состояния можно использовать уравнение Ван-дер-Ваальса

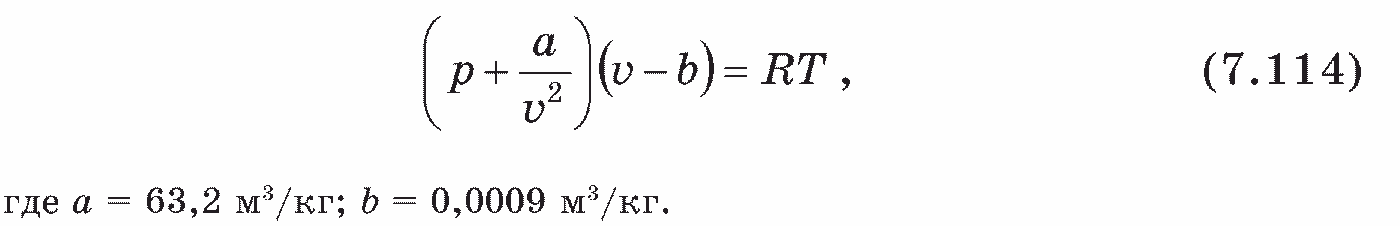
Зависимость между скоростью и удельным объемом пара выражается уравнением неразрывности, которое для стационарного течения имеет вид

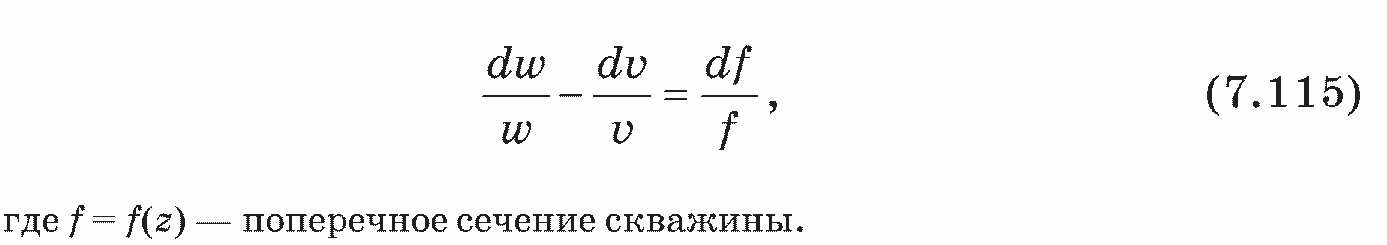
Математическая модель процесса стационарного течения пара в скважине включает следующие уравнения

Для перегретого водяного пара показатель адиабаты изменяется в диапазоне 1,24... 1,35 и в среднем принимается равным 1,3. Следует отметить, что показатель адиабаты на кривой насыщения претерпевает скачок.
Для реальных свойств водяного пара уравнение адиабаты отличается от зависимости (7.117), следовательно, расчет по этому уравнению является приближенным.
Математическая модель изоэнтропического течения имеет вид