3.5.2. Методы расчета ветродвигателей
При исследовании ветродвигателей используют следующие математические модели:
- импульсную теорию идеального ветроколеса;
- теорию элементарных струй, представляющую собой соединение импульсных теорий идеального ветроколеса (т.е. без учтения трения на поверхности ветроколеса) и теорию профиля;
- дисковую вихревую теорию, основанную на законах гидродинамики, определяющую движение и воздействие завихрений.
Заметим, что схемы вихревой теории подобны схемам импульсной, поэтому новых результатов по сравнению с методом элементарных струй в данном методе не ожидается. В связи с этим считаем, что наиболее обоснованным и удобным является метод элементарных струй [60]. Он позволяет значительно расширить изучение и описание физических процессов обтекания ветроколеса.
Выделим элементарный объем, заключенный между двумя трубками тока, секущими диск ветроколеса по окружностям радиусов г и г + dr (рис. 3.17) [17, 60]. Для выделенного контрольного объема запишем законы сохранения импульса и моментов импульса:
![]()


Для исследования ветродвигателей с вертикальной осью вращения используются две аэродинамические теории: импульсные и вихревые.
Импульсные модели.
Основным этапом теории является выведение соотношения, связывающего потерю импульса воздушным потоком, проходящим через омываемую им площадь ветроколеса, со средней потерей времени суммарной аэродинамической силой, действующей на лопасти и определяемой через аэродинамические коэффициенты.
Используются следующие расчетные модели:
- импульсная модель с одной трубкой тока;
- импульсная модель со множеством трубок тока [61];
- импульсная модель, использующая тандем (двойную модель дисковой теории) [62];
- некоторые другие теории [63].
В импульсной модели с одной трубкой тока ротор ветроколеса рассматривается как активный диск, заключенный в одну общую для всего ротора трубку тока. Эта модель необходима лишь для расчета общих характеристик ветродвигателя, таких, например, как коэффициент мощности.
Во второй расчетной модели импульсные соотношения применяются ко множеству элементарных, аэродинамически независимых трубок тока, проходящих через омываемую ротором поверхность. Среди работ, рассматривающих эту модель, следует выделить модель расчета, предложенную В.В. Самсоновым [64]. Задача сводится к системе интегральных уравнений относительно коэффициентов торможения, которая численно решается на ЭВМ методом последовательных приближений.
В модели, применяющей тандем, используются различные коэффициенты интерференции для наветренной и подветренной частей ротора. В других расчетных моделях этой группы обтекание ветроколеса воздушным потоком моделируется с помощью двух последовательно расположенных дисков (система тандем), отбирающих импульсы у проходящих через них потоков.
В работе [63] описана модель расчета, в которой учитывается влияние формы трассы лопастей, состояние атмосферной турбулентности и режим обтекания агрегата в целом. Следуя этой работе, изложим суть одномерной импульсной модели.
Расчетная схема ортогонального ветродвигателя приведена на рис. 3.18.
Принимается допущение, что задача является стационарной. Кроме того, предполагается, что лопасти ротора ветродвигателя испытывают при своем движении такое же силовое движение со стороны потока воздуха, как и изолированное крыло той же длины и с теми же значениями угла атаки. Набегающий поток считается постоянным и равномерно распределенным по размаху лопастей.

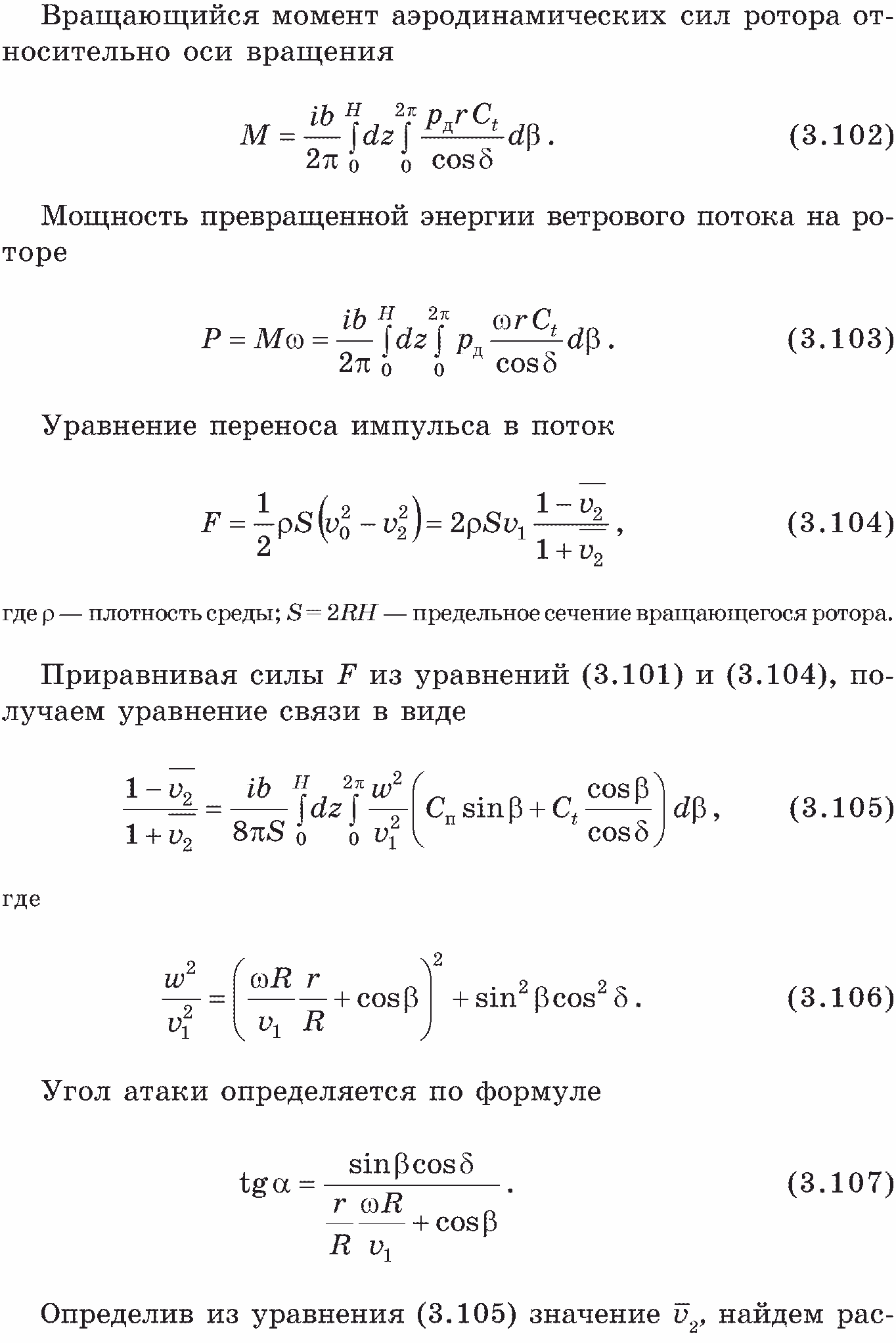
Расчетное выражение для коэффициента быстроходности Θ, коэффициента лобового сопротивления С и коэффициента мощности Ср:
150
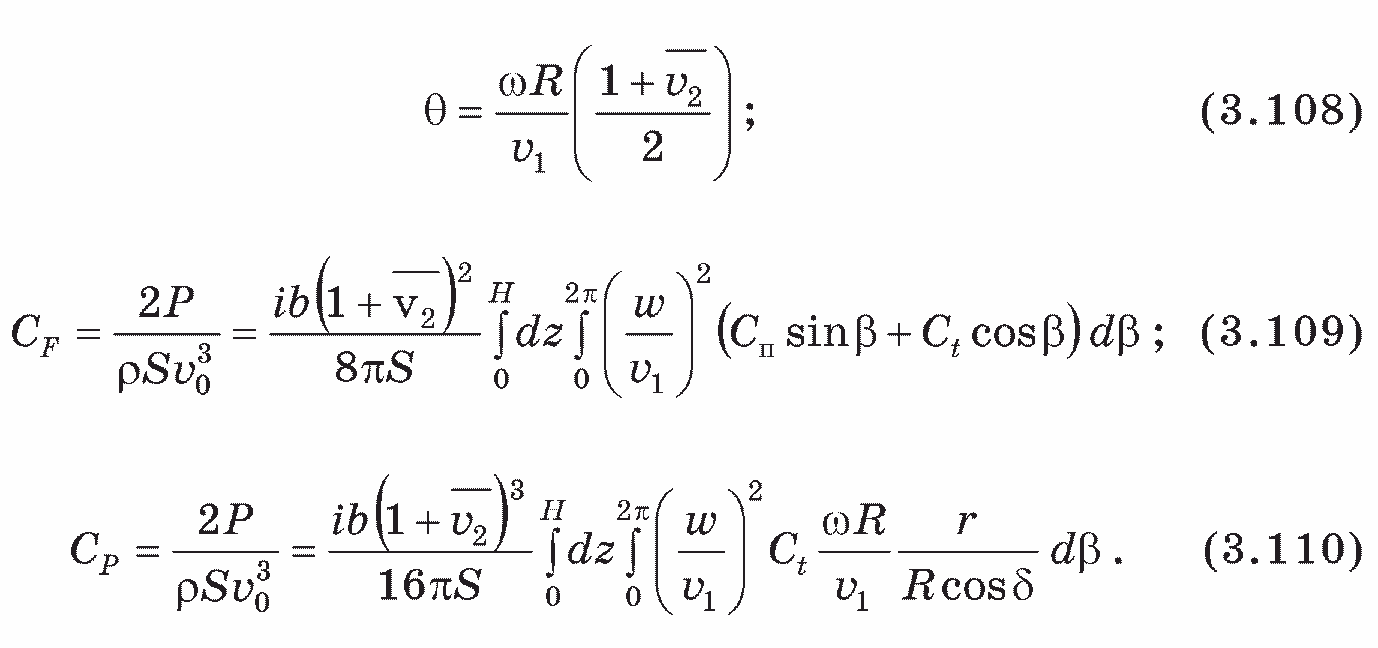
Следует указать, что в тех случаях, когда лопасти ветроколеса расположены параллельно оси вращения, приведенными выше формулами можно пользоваться, приняв г = Rh = Rв = R и δ = 0 (см. рис. 3.18).
Вихревые модели.
Аэродинамические характеристики ветродвигателей типа Дарье можно определить на основе метода построения вихревой модели вращающегося ротора. Основные положения этой теории разработаны достаточно полно [65, 68]. Приложение метода дискретных вихрей к расчетам ветродвигателей вертикально-осевого типа было сделано рядом авторов [67-69].
В первом приближении принимается, что нестационарный поток безотрывно обтекает лопасти ветроколеса. Ветроколесо представляется состоящим из нескольких, размещенных по окружности прямых, параллельных оси вращения лопастей бесконечного размаха, имеющих тонкий симметричный профиль. Задачу считают плоской, среду полагают невязкой несжимаемой. Суммарные дискретные вихри размещают вдоль хорды каждого профиля, свободные вихри — за кромкой профиля на линии хорды. Интенсивность суммарных вихрей на профиле лопасти определяется в контрольных точках, которые размещены вдоль хорды каждого профиля. Свободные вихри в среде движутся вместе с ее частицами, а их интенсивность сохраняется неизменной во времени.
Исходя из указанных предпосылок, получают систему уравнений, определяющую интенсивность суммарных и свободных вихрей [67].
В последнее время предложены конструкции ортогональных ветродвигателей с лопастями, имеющими профиль крылового незамкнутого типа (КН) [70]. Они применимы для маломощных ветроагрегатов. Методика их расчета не отличается от изложенных выше методов, применяемых для определения аэродинамических характеристик лопастей ветроколес вертикально-осевого типа.
Методика анализа аэродинамических характеристик и расчета лопастей ветродвигателей нуждается в дальнейшем развитии. Поток нужно рассматривать как вязкую среду, течение отрывное. Подобная модель ближе к реальной картине. Расчетом пограничного слоя можно определить расположение зон отрыва и, следовательно, дать рекомендации по улучшению аэродинамических характеристик лопастей (профили, для которых зоны отрыва расположены возможно ниже по течению потока). Кроме того, в расчетах надо учитывать характеристики приземного потока ветра, так как именно такой поток поступает к ветроколесу. Желательно также учитывать нестационарный характер воздушного потока. В первом приближении рекомендуется исходить из кусочно-однородной модели, которая может рассматриваться как достаточно близкое приближение к нестационарному течению.

