Один из путей энергосбережения при передаче и трансформации тепловых потоков заключается в применении тепловых труб, которые характеризуются рядом преимуществ: низким
термическим сопротивлением, не требуют дополнительных затрат энергии на передачу теплоносителя [66].
В работе [67] для оптимизации тепловых труб введены функции
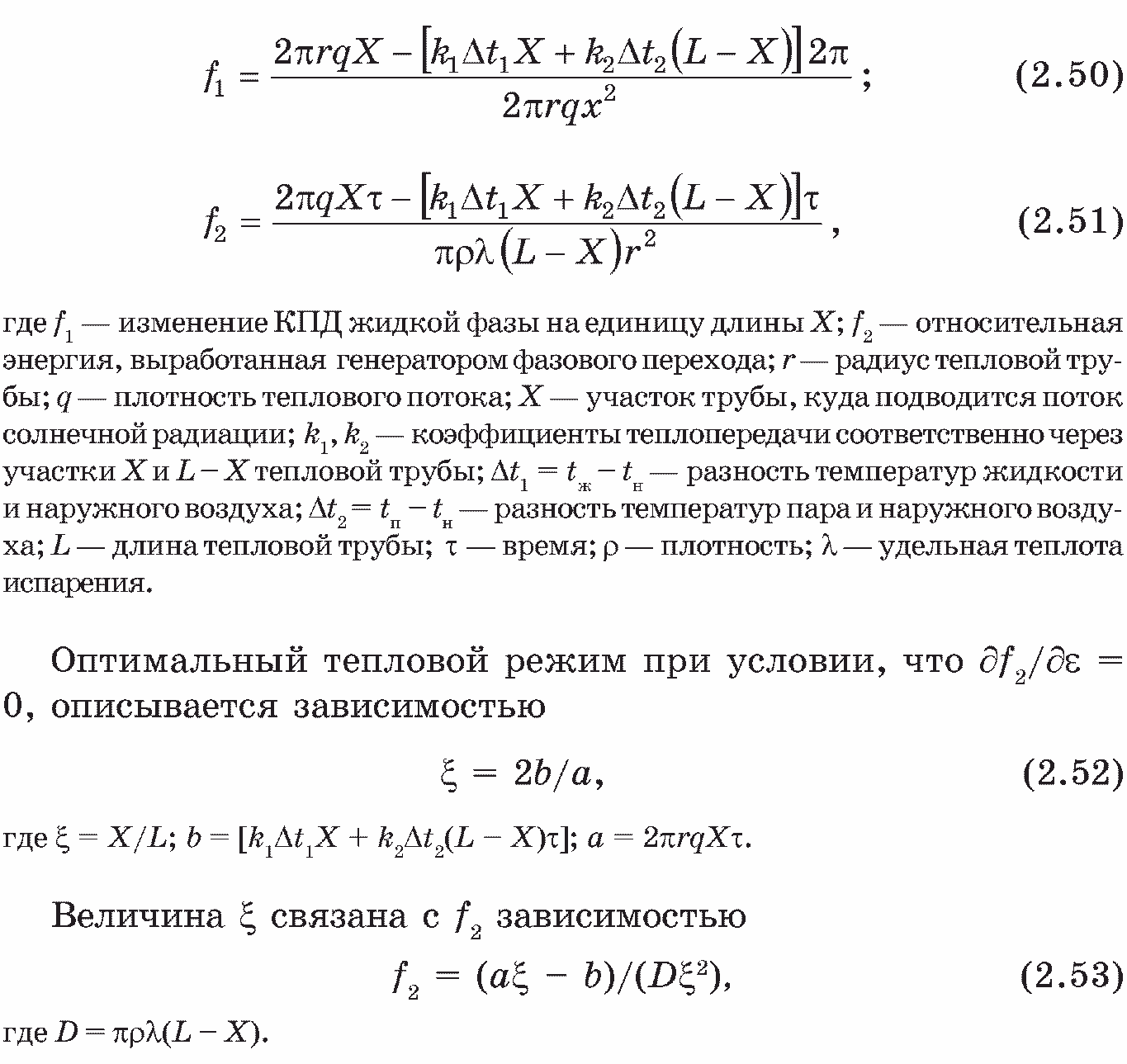
Надо признать, что невзирая на ряд существенных преимуществ, тепловые трубы в качестве теплообменных аппаратов не нашли должного применения в сельскохозяйственной технике. Несомненно, что технико-экономически обоснованное использование тепловых труб в системе энергоснабжения сельского хозяйства окажется весьма эффективным.
Методам расчета и выбора оптимальных параметров теплообменных аппаратов на тепловых трубах посвящен ряд работ, среди которых следует выделить [60, 68-71]. Заслуживает внимания методика теплотехнического расчета теплообменников на тепловых трубах, изложенная в работе [72].

Если принять обозначение
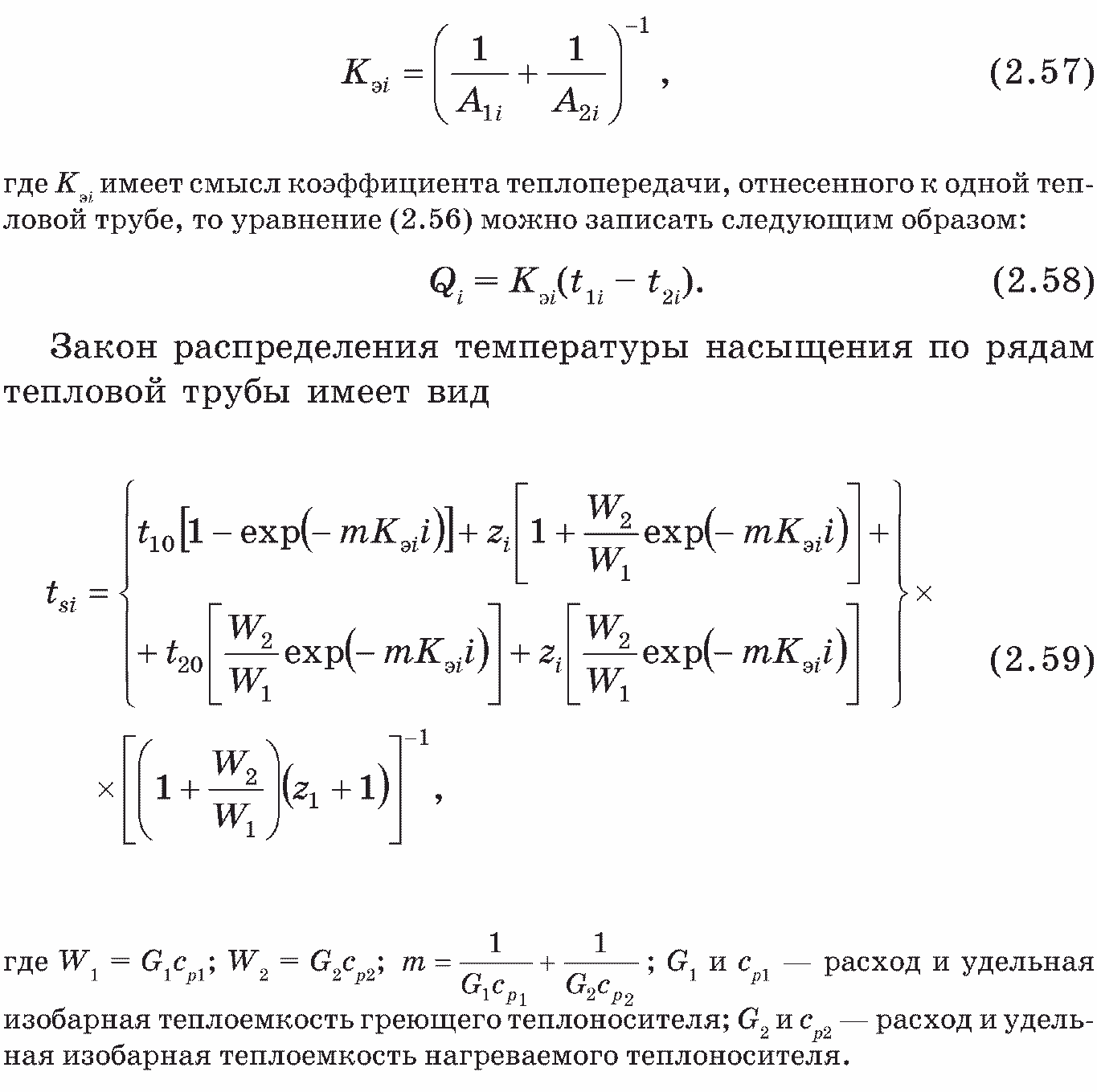
Уравнение (2.56) справедливо при постоянстве значений т, W1 , W2 и z. Такое предположение вполне допустимо для незначительных перепадов температур, что, как правило, характерно для процессов теплообмена, имеющих место в сельскохозяйственных технических устройствах.
Рассмотрим задачу оптимизации теплообменных аппаратов с тепловыми трубами.
Эффективность таких аппаратов в значительной степени зависит не только от внешних условий теплообмена, но и от параметров тепловых труб, используемых в них.
Выбору оптимальных параметров должно предшествовать определение целевой функции. При этом основными являются требования обеспечения минимума материальных затрат и энергопотребления или, в общем случае, рентабельность приведенных затрат. Задача заключается в том, чтобы добиться минимальной массы, приходящейся на единицу передаваемой теплоты m/Q и минимальных удельных затрат N/Q на прокачку теплоносителя.
С увеличением расхода теплоносителя возрастает коэффициент теплопередачи. Вместе с тем возрастание расхода теплоносителя повышает необходимую мощность для его прокачки. Следовательно, существует расход теплоносителя, при котором достигается минимум энергопотребления.
Обоснованный выбор основных параметров теплообменных аппаратов на тепловых трубах требует постановки и решения соответствующей оптимизационной задачи, т.е. определения минимума комплексной функции вида [72]

Полученную поверхность теплообмена теплообменного аппарата с тепловыми трубами можно рассчитать из известного интегрального соотношения

Отсюда следует

(2.67)
В результате приходим к известной задаче нелинейного программирования:
![]()
(2.68)
которая решается численными методами (методы Лагранжа— Понтрягина, Гамильтона—Якоби—Веллмана и др.) [74].
Принцип максимума Понтрягина относится к задаче оптимального управления. Наиболее полное решение этой задачи получено для линейных систем, где соотношения принципа максимума Понтрягина часто выступает не только как необходимое, но и как достаточное условие оптимальности [75]. Принцип максимума Понтрягина получил многочисленные обобщения в различных сложных задачах.
Теория Гамильтона—Якоби относится к вариационному исчислению, в котором нахождение экстремума функций сводится к интегрированию уравнения с частными производными первого порядка [76].

