Оптимизация с-х энергетических установок - Основы оптимизации абсорбционных термотрансформаторов

Наиболее перспективным для разработки основ структурного анализа, синтеза и оптимизации является теоретикографовый метод. В последние годы этот метод был дополнен анализом в терминах современной прикладной термодинамики [59].

Потоковые графы, вершины которых отображают элементы системы, а дуги — физические потоки, являются наглядными и удобными для проведения вариантных расчетов и параметрической оптимизации, что служит основой для создания пакета прикладных программ.
Задача оптимизации — минимизировать значение целевой функции

(5.69)

Рис. 5.28. Схема геотермальной системы теплохладоснабжения с абсорбционным термотрансформатором:
1 — эксплуатационная скважина; 2, 6, 8, 15, 20 — насосы; 3 — фильтр; 4 — скоростные теплообменники; 5,11 — потребители тепла; 7 — теплообменники; 9 — генератор термотрансформатора; 10 — конденсатор; 12 — теплообменник; 13,17 — дроссельные вентили; 14 — абсорбер; 16, 22 — потребители холода; 18 — испаритель; 19 — сборный бак; 21 — нагнетательная скважина

для всех ij, принадлежащих сети, где Z — вес дуги, т.е. затраты в блоке (цикле), которые соответствуют данной дуге с принятыми граничными условиями. При этом X.. = 1, если дуга ij ч
входит в рассматриваемый путь, X = 0 — в противном случае.
На рис. 5.28 изображена схема геотермальной системы тепло-хладоснабжения потребителей. Для повышения эффективности установки в схему включен абсорбционный термотрансформатор.
Для математического моделирования применяют топологические модели различных классов, в данном случае — параметрические потоковые графы, при помощи которых разрабатывают алгоритмы оптимального анализа или синтеза энергетических систем. Цифровым описанием служит матрица инциденций, которая полностью отражает топологическую структуру информационной схемы и позволяет перенести ее на язык алгебры или теории множеств.
В матрице инциденций прослеживается связь по диагональному заполнению булевыми переменными. Левый столбец матрицы содержит номер блока, остальные — номера потоков информационной схемы. Сканируя по строкам матрицы инциденций при помощи ЭВМ, находят значения параметров тепловых и массовых потоков, а также потери эксергии в элементах системы, определяют степень энергетического совершенства системы.
Параметрический потоковый граф, отображающий топологию схемы, показанной на рис. 5.28, а также соответствующая матрица инциденций, представлены на рис. 5.29.
Эксергетический потоковый граф и матрица инциденций, построенные для анализируемой схемы, показаны на рис. 5.30.
Алгоритм оптимизации энергосберегающих систем строится на основе структурного анализа параметрического потокового графа. При этом многоконтурный исходный ППГ превращают в эквивалентный ациклический ППГ, который является упорядоченным по слоям вершин орграфов. Тем самым при выбранных особых дугах в структуре исходного многоконтурного ППГ устанавливается порядок расчета математических моделей отдельных элементов изучаемой системы, соответствующих вершинам ППГ. Задача оптимизации формулируется следующим образом. Дан исходный многоконтурный ППГ, который содержит п разно-параметрических дуг Е

которые разрывают все т простых контуров в исходном ППГ.

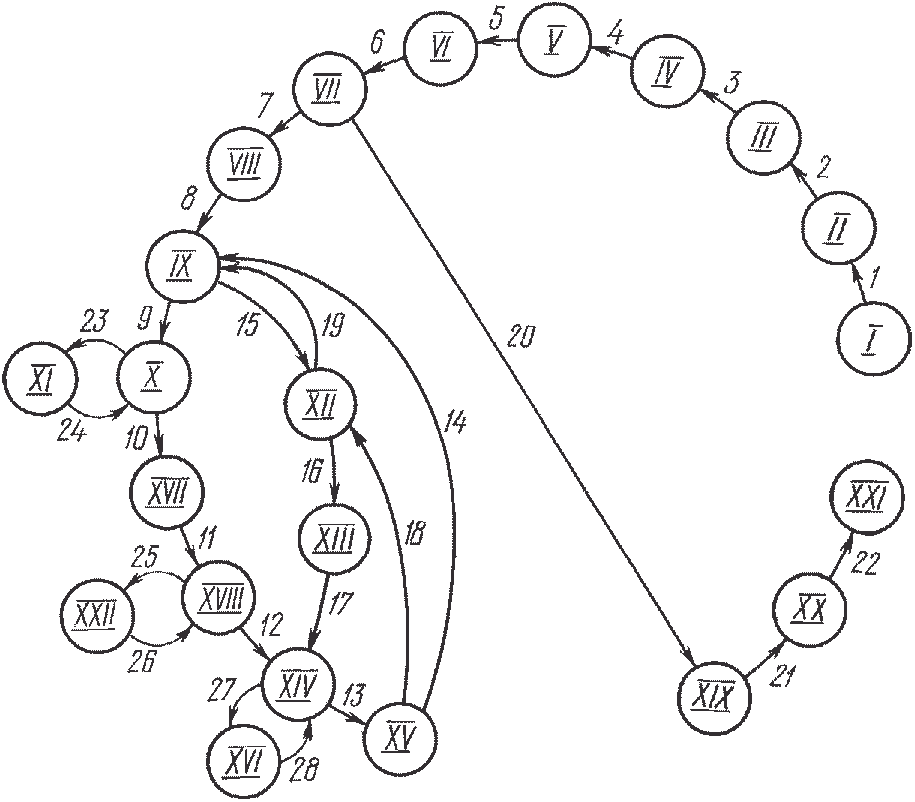
Рис. 5.29. Параметрический потоковый граф и соответствующая матрица инциденций (см. стр. 301) для схемы, изображенной на рис. 5.28
Этим самым многоконтурный ППГ превращается в эквивалентный ациклический граф. Причем ставится условие, что не существует никакого другого подмножества
Е*, обладающего тем же свойством (здесь Е* — минимальное множество особых дуг, удовлетворяющих условию (5.70)).
Если все дуги исходного ППГ одинаково параметричны, то уравнение (5.70) записывается следующим образом: р = min.
В качестве критерия эффективности можно принять ту или иную характеристику системы: экономическую, энергетическую, технологическую или др. Задача оптимизации, как правило, считается однокритериальной и решается путем выбора из многих критериев одного доминирующего с введением ограничений на остальные. При выборе более одного критерия эффективности (обычно двух критериев) оптимизацию проводят сначала по одному, а затем по другому критерию. При двухкритериальном анализе можно пользоваться одним обобщенным критерием [60]. Предварительные варианты выбираются эвристически, исходя из данных проектирования и накопленного опыта.
В некоторых случаях следует выделять локальные критерии для отдельных элементов или подсистем, их связи с доминирующим критерием.

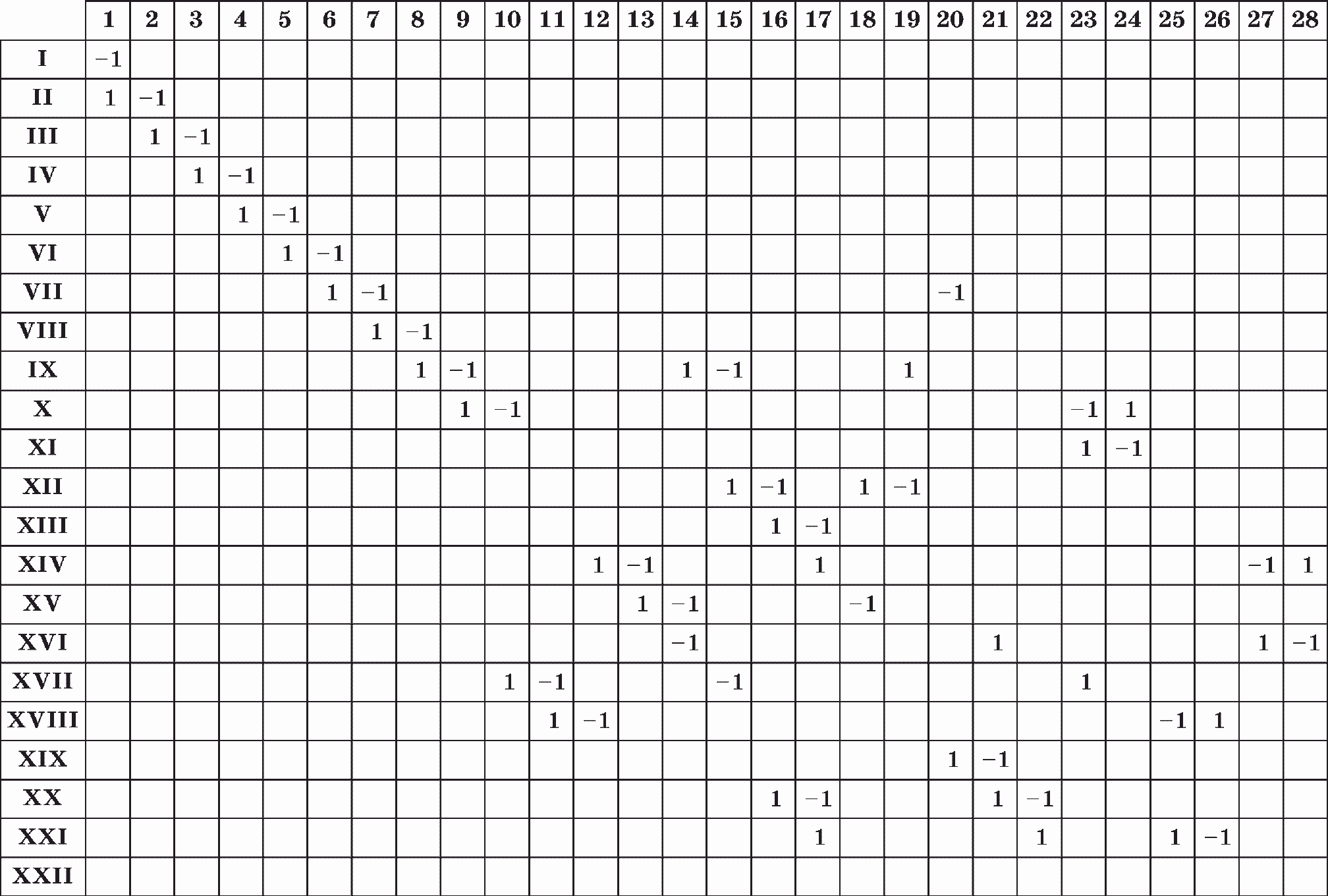
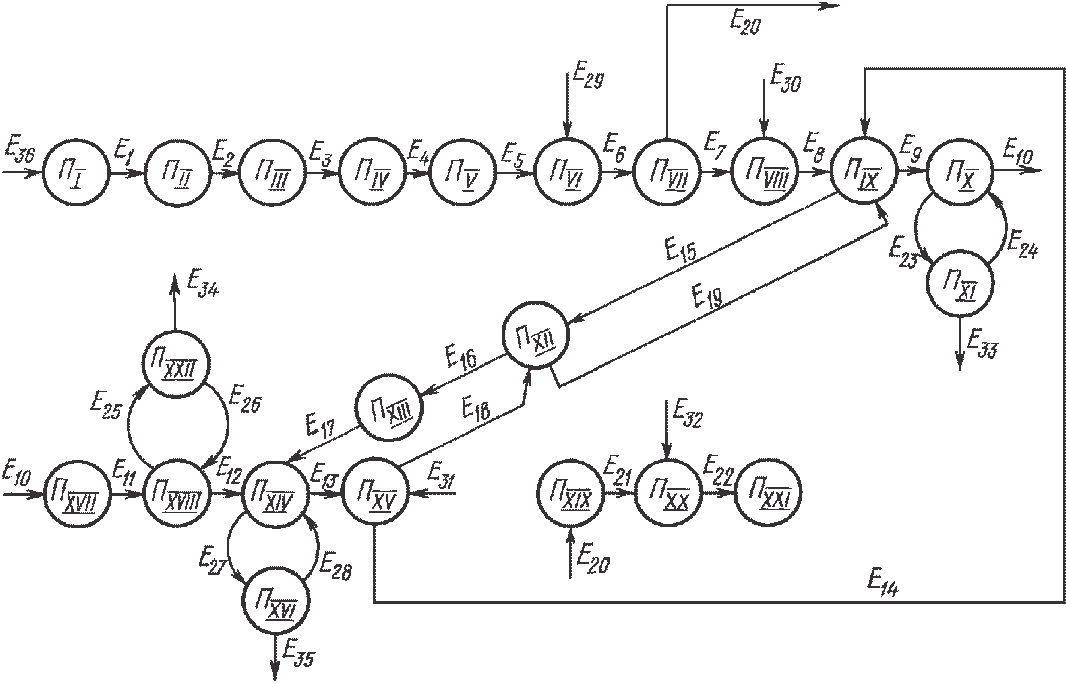
Рис. 5.30. Эксергетический потоковый граф и матрица инциденций (см. стр. 303) для схемы, изображенной на рис. 5.28
Для энергетических систем основным критерием эффективности обычно являются преобразование потоков эксергии в системе, а также термодинамическая степень совершенства функционирования системы и ее отдельных элементов. При таком подходе оптимум решения определяется условием, что потери эксергии минимальны:
(5.71)
На рис. 5.31 представлена схема геотермального теплоснабжения потребителей [60]. В схеме предусмотрены два понижающих абсорбционных термотрансформатора (АТТ). Система преобразования теплоты геотермальных источников в элементах теплонасосной системы, а также температурные режимы и теплопроизводительность каждого элемента представлены на диаграмме потоков энергии Грассмана (рис. 5.32). Невозможность непосредственного использования геотермальной воды в системе отопления и горячего водоснабжения описана авторами в работе [59].
Исходя из вышеизложенного, представленную энергетическую систему будем анализировать в терминах эксергономики.

Рис. 5.31. Принципиальная схема геотермального теплоснабжения на базе теплоиспользующего теплового насоса:
А — абсорбер; БА — баки-аккумуляторы; Гр — градирня; Г — генераторы АТТ; И — испарители; Кт — котельная; К — конденсаторы АТТ; ТО — теплообменники; Н — насосы; П — потребители; СН — скважина нагнетательная, СЭ — скважина эксплуатационная

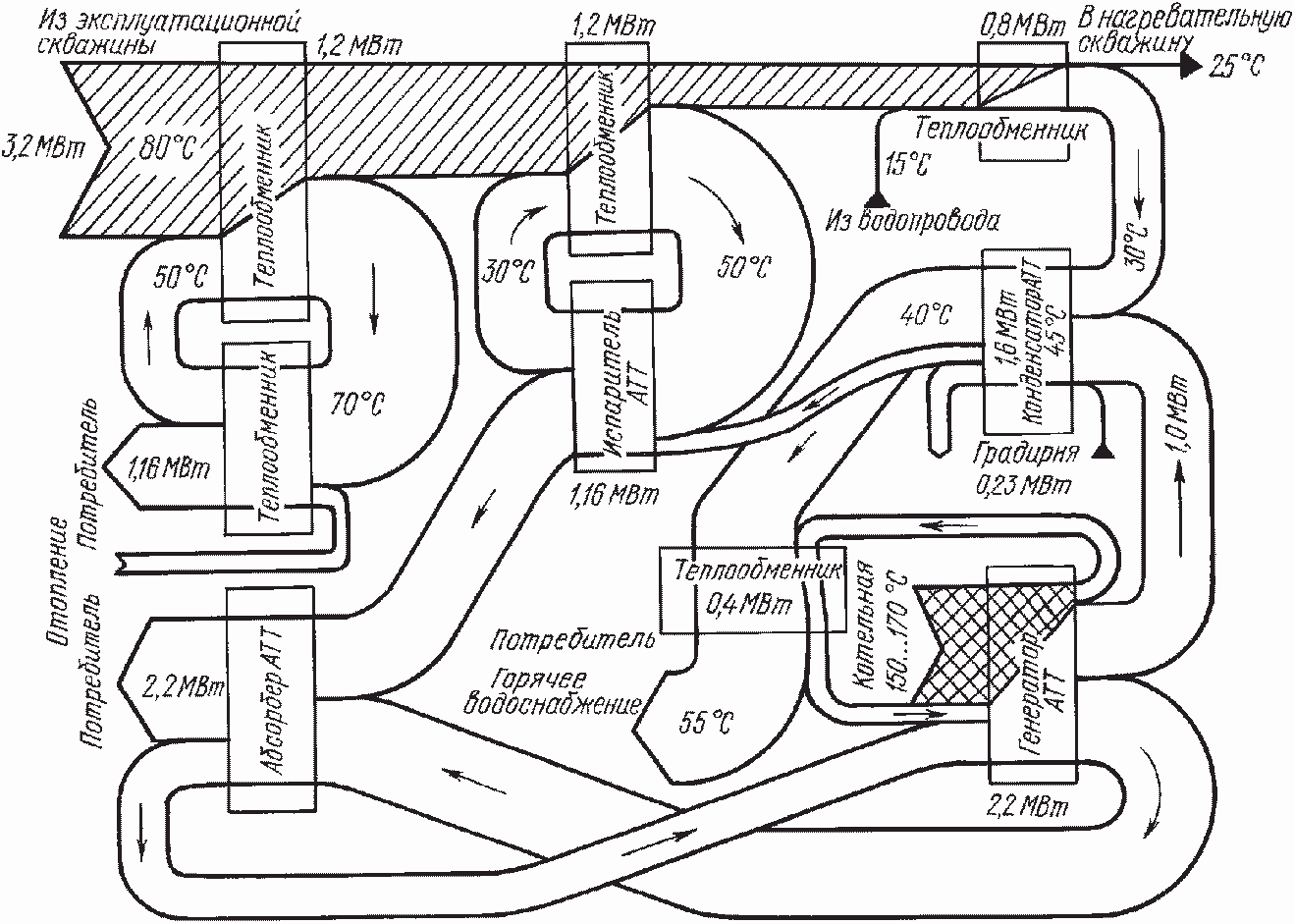
Рис. 5.32. Диаграмма потоков энергии Грассмана для схемы, изображенной на рис. 5.31
При анализе энергетических систем в качестве оптимизационных критериев используют энергетические показатели (эксергетический КПД, степень термодинамического или тепломассообменного совершенства).
Уравнение эксергетического баланса для энергетической системы можно записать в следующем виде

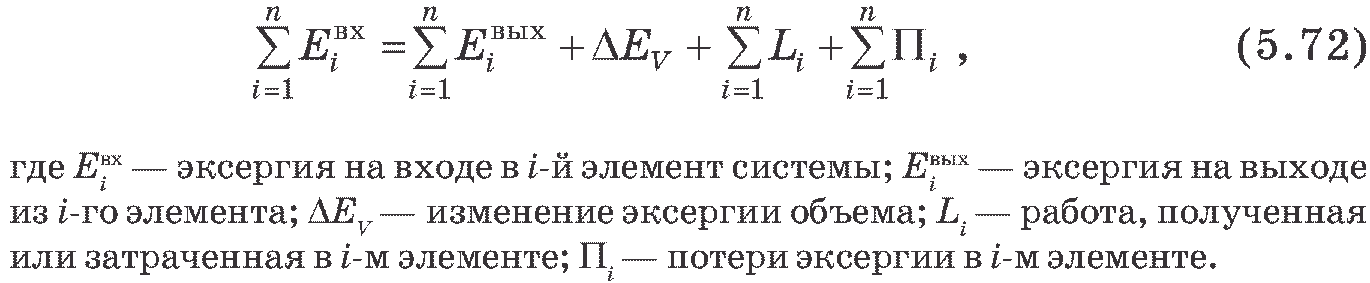
Величина Е применима для изучения систем, где совершаются процессы периодического характера.
Более строгий эксергетический анализ можно выполнить при использовании понятия внутренней эксергии, вытекающей из основных положений неравновесной термодинамики. Она измеряется обратимой работой, которую необходимо затратить, чтобы перевести эту систему из состояния внутреннего равновесия в данное неравновесное состояние, не изменяя положения системы относительно окружающей среды.
Для внутренней эксергии можно записать [57]

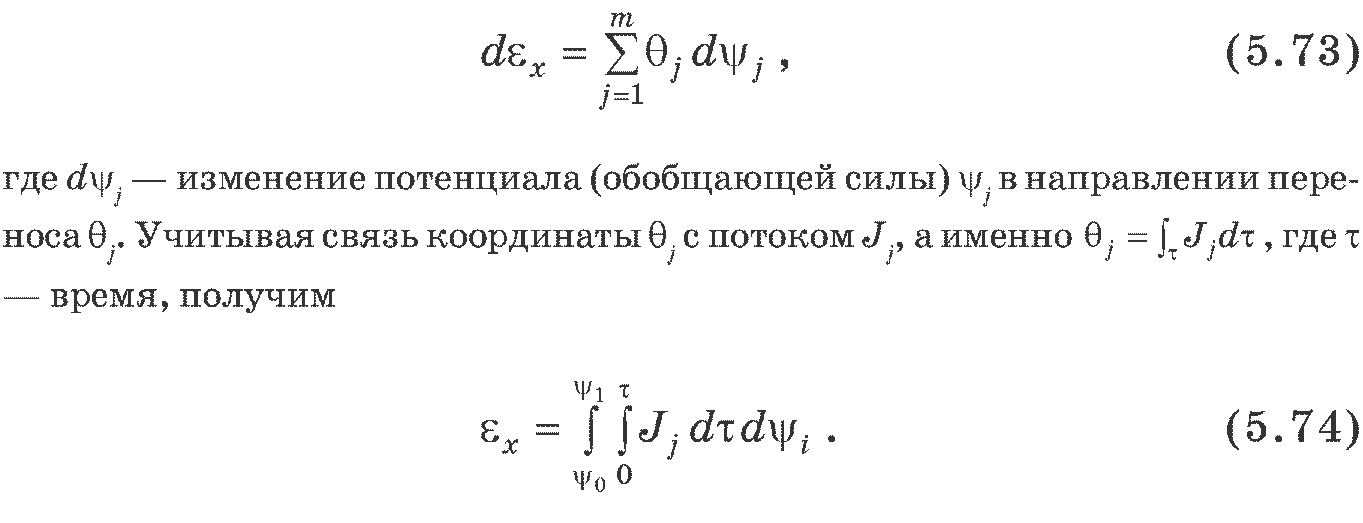
Уравнение (5.73) определяет эксергию потока теплоты, а уравнение (5.74) — эксергию рабочего тела. Таким образом, мы можем оценить энергетические характеристики системы при переносе как вещества, так и теплоты.
Отмечено [14], что потери эксергии при параллельном соединении элементов эквивалентны. Кроме того, рассматриваемая энергетическая система представляет собой набор теплообменных аппаратов, работающих при температурах, близких к нулевому значению эксергетической эмиссии. В связи с этим величина П. в каждом элементе является равнозначной и отпадает необходимость определять ее при увеличении порядкового номера элемента в процессе продвижении от «начала» до «конца» цикла эксергопреобразования.
Схема теплохладоснабжения установки с абсорбционным термотрансформатором показана на рис. 5.33. Источником энергии служат ветродвигатель и солнечная энергия. Схемой предусмотрено наличие аккумуляторов теплоты.
В связи с необходимостью иметь наипростейший вид рассматриваемой схемы в теории графов применяется метод эквивалентирования. Это замена реальной системы или ее элементов некоторой приближенной, абстрагированной, упрощенной моделью, эквивалентной относительно функционирования и свойств. Этот принцип рассмотрения системы необходим ввиду практической невозможности количественно описать некоторые элементы и связи с помощью существующих математических методов.

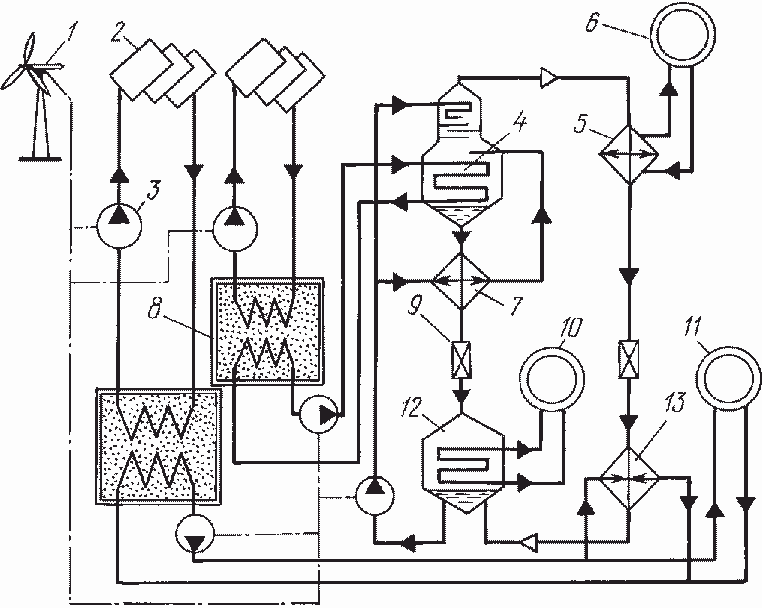
Рис. 5.33. Схема теплохладоснабжения с абсорбционным термотрансформатором: 1 — ветродвигатель; 2 — солнечные коллекторы; 3 — насосы; 4 — генератор с дефлегматором; 5 — конденсатор; 6 — потребитель холода; 7 — теплообменник раствора; 8 — аккумулятор теплоты; 9 — дроссельные вентили; 10 — потребитель холода; 11 — потребитель теплоты; 12 — абсорбер; 13 — испаритель

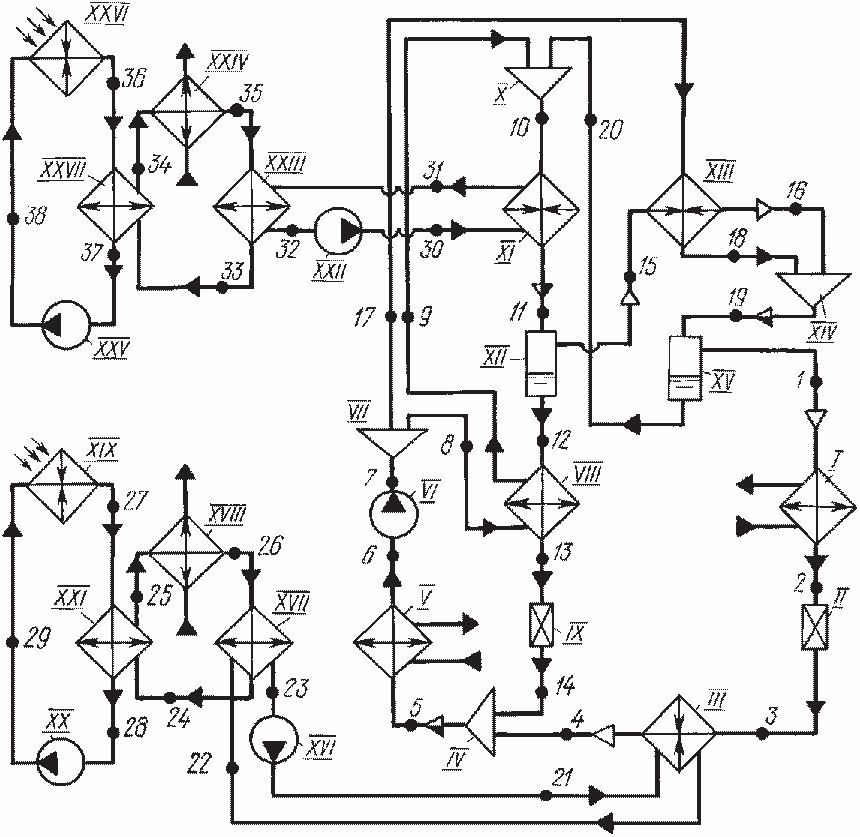
Рис. 5.34. Информационная схема схемы, приведенной на рис. 5.33
На рис. 5.34 представлена информационная схема системы солнечного тепло- и хладоснабжения. Для прочтения этой схемы воспользуемся табл. 5.8.
Таблица 5.8. Элементы и соответствующие им эквиваленты по информационной схеме системы (см. рис. 5.34)

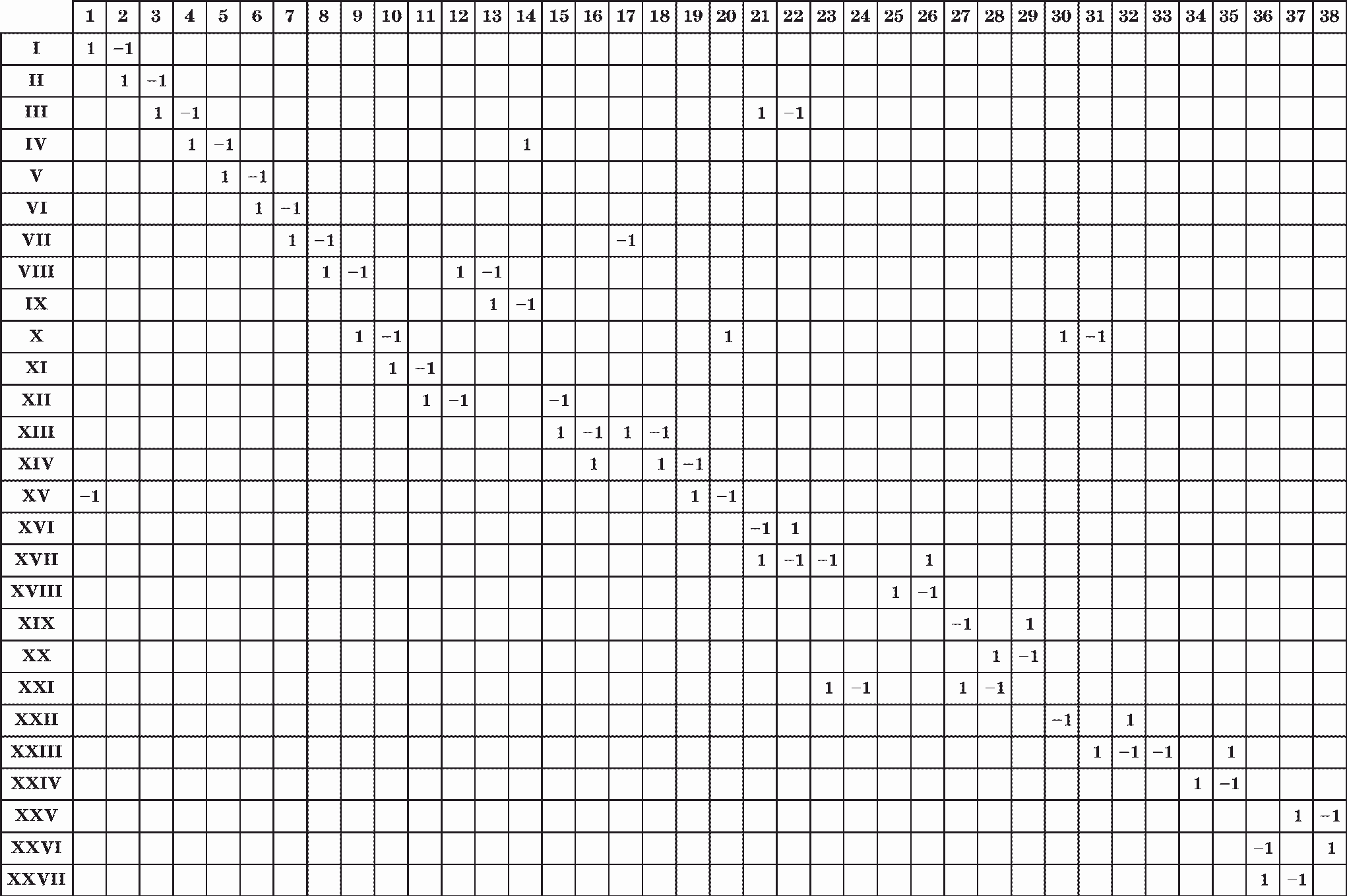
Потоковый параметрический граф и соответствующая ему матрица инциденций представлены на рис. 5.35. Этот граф удобен для организации расчетов и анализа свойств системы как при «ручном» расчете, так и при расчетах на ЭВМ.
Если рассматриваем более простые схемные решения (без аккумулятора теплоты низкого потенциала, без ветроэнергетической установки и т.д.), «отключением» соответствующие элементы и связи в информационной схеме и приравниваем нулю вершины и дуги в графе.
Граф (рис. 5.35) состоит из трех блоков с двумя точками сочленения III и XI. Декомпозиция графа по этим точкам приводит к трем порожденным подграфам, которые описывают топологию каждой ветви отдельно, т.е. описывают абсорбционный тепловой насос, высокопотенциальную и низкопотенциальную системы солнечной энергии. Связность графа прослеживается внутри каждого контура. Таким образом, разрыв связей 21 и 22 вершины III и связей 30, 31 вершины XI не противоречит теории графов и дает возможность, в случае необходимости, анализировать каждый контур отдельно. Аккумуляторы теплоты поддерживают на постоянном уровне параметры потоков 21, 22 и 30, 31, следовательно, при расчетах теплонасосного контура эти параметры можно считать заданными.

Рис. 5.35. Потоковый параметрический граф и матрица инциденций (см. стр. 309) схемы, приведенной на рис. 5.34

Высокую эффективность работы рассматриваемой системы солнечного тепло- и хладоснабжения можно получить при использовании высокоэффективных абсорбционных тепловых насосов с большой степенью внутренней регенерации. В этом случае, в зависимости от заданных входящих и выходящих потоков (для потребителя), можно оптимизировать работу абсорбционного теплового насоса по минимальной теплоте генерации и приводной электрической мощности для насоса. Система солнечного тепло- и хладоснабжения имеет локальный максимум на участке местных климатических условий. Тепловой насос подвергается глобальной оптимизации в локальной для системы зоне. Таким образом, оптимизация рассматриваемой системы имеет характер вложенности.
Традиционно математическая модель должна пройти экспериментальное подтверждение. Если модель построена на основе теоретико-графовых методов, то отпадает необходимость в создании полной системы. Вполне достаточно проверить адекватность модели на отдельном элементе по математической модели этого же элемента.

Рис. 5.36. Эксергетический потоковый граф и матрица инциденций для гелиосистемы

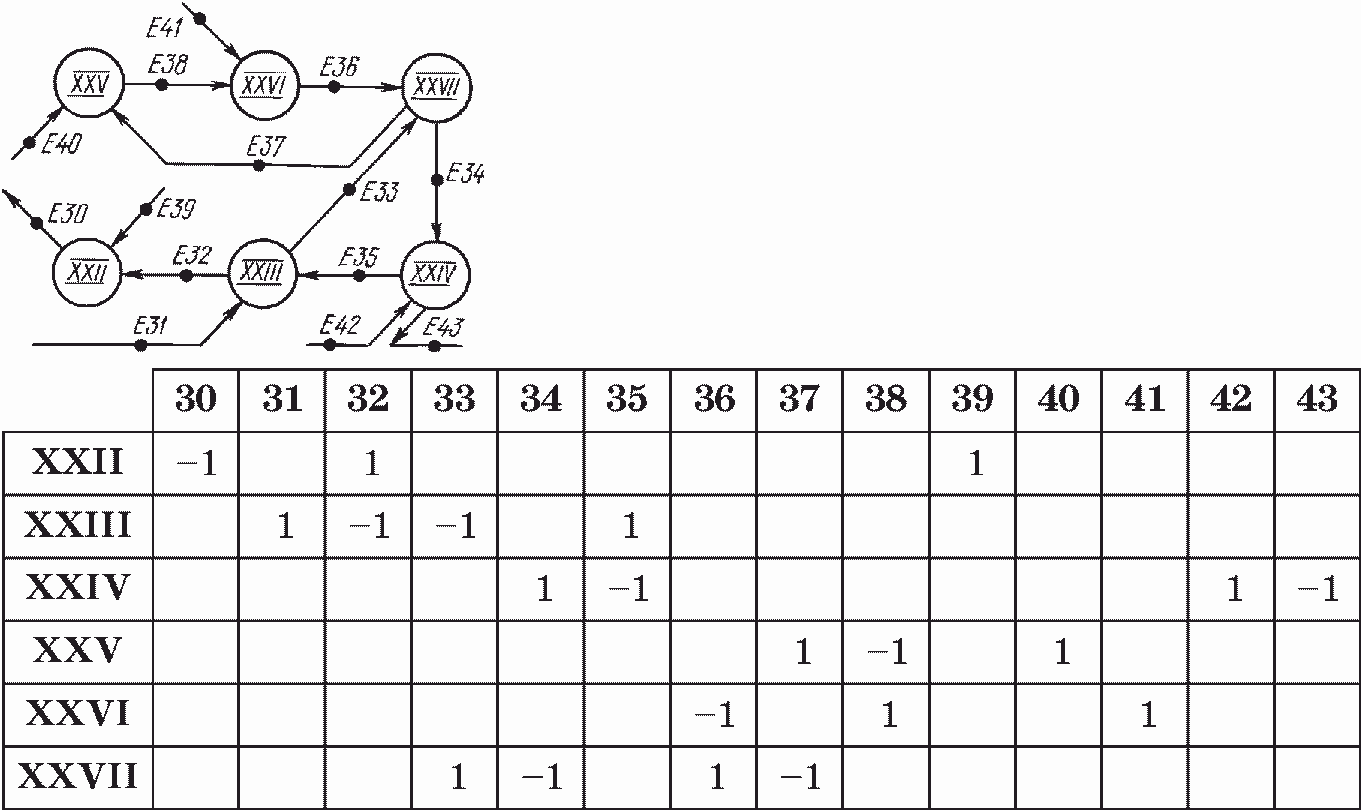
Адекватность математической модели системы солнечного тепло- и хладоснабжения проверена на примере солнечных коллекторов разных конструкций. Для организации автоматизированных расчетов разработаны эксергетический потоковый граф гелиосистемы и соответствующая ему матрица инциденций (рис. 5.36).
Для максимального охвата территории страны, где целесообразно применять гелиосистемы, авторами приняты следующие климатические условия: 40 °с.ш., 52 °с.ш., 56 °с.ш.
Испытываемые гелиоколлекторы имели одинаковые размеры и равные условия проведения испытаний. Эксперимент проводился с тремя конструкциями поглощающих панелей солнечных коллекторов: плоской, листотрубной и трубчатой на стенде-иммитаторе солнечного излучения. Результаты проверки адекватности математической модели солнечных коллекторов показали хорошее совпадение расчетных и экспериментальных данных (рис. 5.37).

Рис. 5.37. Результаты экспериментальных и расчетных данных зависимости η = f(R), тц,е R - тепловое сопротивление