5.4.3. Гидродинамика двухфазных сред в абсорбционных трансформаторах
Экологически чистый водоаммиачный раствор широко используется в качестве рабочего вещества в термотрансформаторах. От степени совершенства тепломассообменных процессов в элементах сложных и гибридных термотрансформаторов зависят показатели работы всей установки. Гидродинамика двухфазных потоков в термотрансформаторах мало изучена.
В основу исследования гидродинамики многофазных сред могут быть положены несколько математических моделей.
Осредненные уравнения движения для газо- и парожидкостных смесей с учетом фазовых переходов приведены в работе [34]. Более строгий анализ основных осредненных уравнений для отдельных компонент выполнен в работе [35]. В данном случае гидротеплообмен сплошной среды рассматривается в рамках эйлерова континуального подхода, а закономерности движения дисперсной фазы в потоке исследуются в рамках лагранжевого представления. Турбулентные пульсации скорости дисперсных частиц рекомендуется описывать методом стохастического моделирования [36].
Заслуживает внимания теория взаимодействующих континуумов, разработанная Р.И. Нигматулиным [37]. При разработке математической модели гетерофазной среды возникает задача осреднения параметров по некоторому интервалу времени и области пространства. В работе [37] предложен метод общего пространственно-временного осреднения, зависящего от интервала или формы и значений объема области.
В другом методическом подходе [38] принято предположение, что расположение в пространстве, форма и размеры элементов дискретной фазы (капель, пузырьков, частиц) являются случайными величинами. Суть анализа заключается в том, что вводится функция φ(2ρ г9, г3, τ), которая указывает на вероятность того, что в окрестностях данной точки пространства в момент времени τ находится ί-я фаза или что данная точка пространства принадлежит множеству точек i-й фазы. Такая вероятность может быть представлена как объемная концентрация i-й фазы в данной точке пространства.
Движение двухкомпонентных сред проанализировал Х.А. Рахматулин [39]. В уравнение движения он ввел функцию k — функцию взаимодействия между компонентами потока. Аналогичный метод анализа применительно к п компонентам, когда один из компонентов участвует в химических реакциях, рассматривается в работе [40].
Среди работ, посвященных гидродинамике многофазных сред, когда один из компонентов может изменять свое фазовое состояние, следует выделить работы [41, 42].
При формировании многофазного движения в рамках многоскоростного континуума задаются условиями совместного движения фаз и величинами, описывающими внутрифазовые силовые, энергетические и межфазовые (массовое, силовое, энергетическое) взаимодействия.
В тех случаях, когда инерционные эффекты относительно движения фаз несущественны, для описания движения многофазных сред обращаются к диффузному, т.е. одножидкостному, приближению.
Уравнения движения и состояния для всей среды в целом, задающие тензор напряжения и внутреннюю энергию, записываются в предположении локального термодинамического равновесия, когда в каждой точке можно определить температуру среды Т. При этом принимается, что тензор скоростей е*' деформируется и определяется полем барицентрических скоростей смеси υ.

При этом справедливо соотношение Гиббса
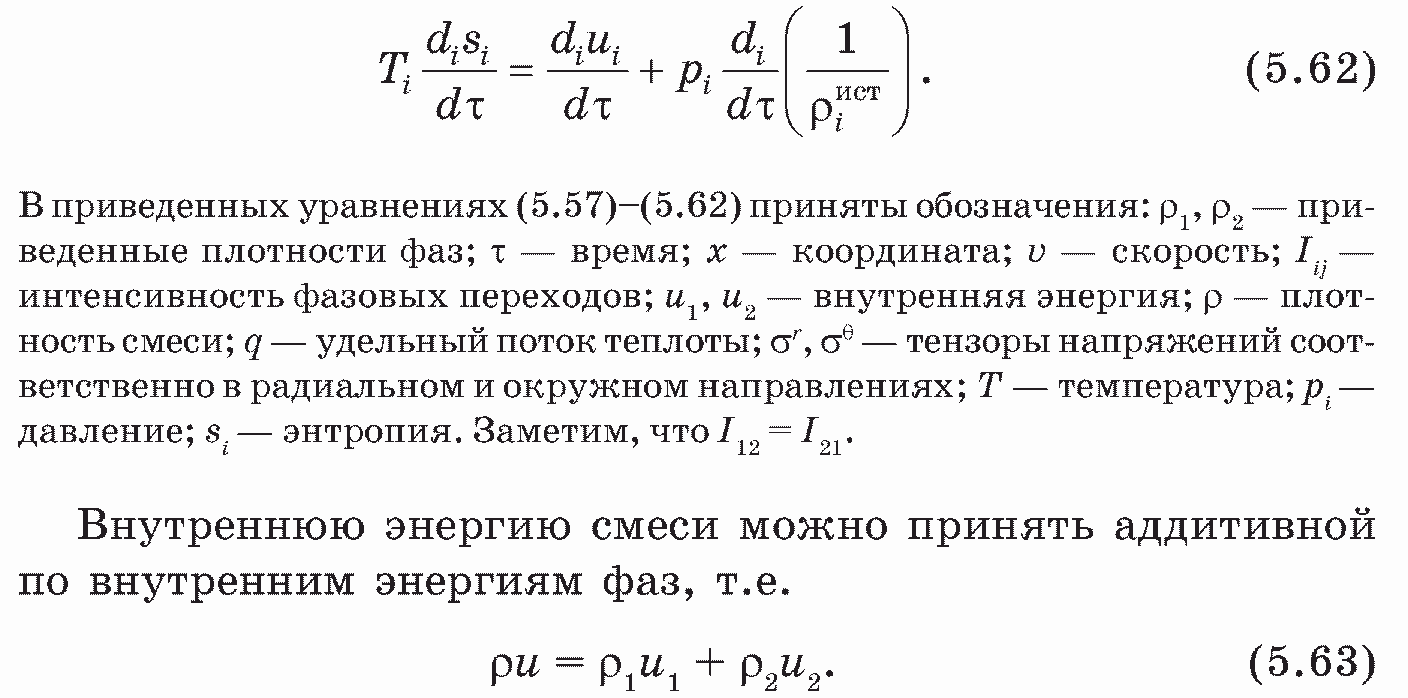
Отметим, что при решении одномерных плоских задач нет необходимости подсчитывать эйлерову координату х точек среды, т.е. интегрировать уравнение (5.60).
Одним из важных разделов динамики двухфазных сред в термотрансформаторе является кинетика конденсации. Конденсация может происходить в том случае, когда парциальное давление пара одного из компонентов смеси в процессе расширения становится большим, чем его давление насыщения.
Одним из первых явление конденсации пара исследовал Стодола. На основе данных экспериментов он показал, что может происходить как гетерогенная, так и гомогенная конденсация. Характер конденсации во многом зависит от промежутка времени, в течение которого создается пересыщение.
Теоретический анализ течений с конденсацией, основанной на концепции образования зародышей (нуклеации), был предложен в работах [44-46]. Эти теоретические принципы, хотя и не охватывают всю совокупность процессов, происходящих при конденсации, в основном согласуются с экспериментом [47].
Упрощенный аналитический метод оценки процесса завершения конденсации предложил Г. Джёрмати [48]. При расчете процесса нуклеации экспериментальные данные хорошо согласуются с расчетными. Нужно заметить, что для быстродвижущейся среды данные измерений в состоянии покоя неприменимы для оценки поверхностного напряжения, поэтому расчетный метод, разработанный в работе [49], имеет ограниченное применение.
В работах [49, 50] предложена система уравнений, описывающая течение смеси из п компонентов, один из которых может конденсироваться. В систему уравнений входит кинетическое соотношение для функции распределения капель по размерам. Кроме того, определены значения коэффициентов конденсации а и термической аккомодации β, предложенных для процессов конденсации П. Хиллом [51].
Процесс нуклеации является составной частью процесса конденсации. Одновременно происходят сложные процессы тепломассообмена. Более подробно эти процессы анализируются в работах [52, 53].
Для условий стационарной нуклеации М. Фольмер [54] определяет скорость образования зародышей Γν как произведение числа молекул пара 7V в единице объема на количество молекул Ъ, конденсирующихся при столкновении с единицей поверхности в единицу времени, и на поверхность зародыша, т.е.
![]() (5.64)
(5.64)
где /? — постоянная Больцмана; у — коэффициент поверхностного натяжения жидкости, который считается не зависящим от радиуса г капли; В — безразмерный множитель.
На основе кинетической теории [51] значение Ъ определяется по формуле
![]() (5.65)
(5.65)
где ак — коэффициент конденсации, равный отношению числа конденсирующихся молекул пара к числу падающих молекул на поверхность среды; р — давление; т, — масса молекулы, равная отношению молекулярной массы к числу Авогардо.
Безразмерный множитель


