Теория графов — область дискретной математики, особенностью которой является геометрический подход к изучению объектов и явлений [2, 3]. Она связана со многими областями математики — теорией множеств, математической логикой, комбинаторикой и пр. При исследовании графов случайных используются методы теории вероятности.
Характеризуя проблематику теории графов, можно отметить, что некоторые направления приложения этой теории имеют более комбинаторный характер, другие — более геометрический. К первым относятся, к примеру, задачи о построении графов с заданными свойствами. Геометрический (топологический) характер имеют многие группы задач. К ним относятся графов отходы, имеющие приложения в технических и экономических задачах, а также графов укладка, которые используются при автоматическом проектировании.
В теории графов существуют специфические методы решения экстремальных задач. Для конечных графов, т.е. для графов с конечным множеством вершин и ребер, проблема существования алгоритма решения задач, в том числе экстремальных, чаще всего, как правило, решается положительно. Построение эффективных алгоритмов, находящих решение с требуемой степенью точности, для теории графов имеет существенное значение.
Для решения задач математического моделирования, анализа и оптимизации энергетических систем обращаются к топологическим моделям системы. Они позволяют установить зависимость взаимосвязи между изменениями технологической топологии и количественными характеристиками изучаемой системы от входных переменных, воздействующих на систему.
Можно выделить четыре группы потоковых графов энергосберегающих систем: параметрические потоковые графы (ППГ); материальные потоковые графы (МПГ); тепловые потоковые графы (ТПГ) и эксергетические потоковые графы (ЭПГ). При решении оптимизационной задачи для энергосберегающих систем в первую очередь будем обращаться к параметрическому потоковому графу.
Параметрические потоковые графы — это взвешенные по дугам и вершинам связные орграфы, отображающие преобразование элементами исследуемой системы параметров физических потоков системы. Вершины ППГ отображают элементы (технологические операторы) системы, а также точки стыковки технологических трубопроводов, источники и стоки физических потоков системы. Вес каждой вершины ППГ соответствует системе уравнений математической модели изучаемой установки. Дуги ППГ соответствуют физическим потокам (массы, теплоты, энергии) системы.
Эксергетические потоковые графы — это взвешенные по дугам связные орграфы, отображающие преобразование элементами рассматриваемой системы расходов эксергии потоков вещества и энергии, а также потери эксергии в элементах системы. Вершины ЭПГ соответствуют элементам (технологическим), которые преобразовывают расходы эксергии, а также источникам и стокам эксергии. Дуги ЭПГ соответствуют потокам эксергии, а также потерям эксергии в элементах системы. Вес дуг равен расходам эксергии. Для каждой вершины ЭПГ справедливо уравнение баланса эксергии.
Материальные потоковые графы — это взвешенные по дугам орграфы, которые отображают преобразование элементами (технологическими операторами) массовых расходов физических потоков системы. Вершины МПГ соответствуют: технологическим операторам системы, которые трансформируют массовые расходы физических потоков; точкам стыковки трубопроводов; источникам и стокам вещества физических потоков. Дуги МПГ соответствуют физическим потокам энергетической системы (ЭС).
Тепловые потоковые графы — это взвешенные по дугам связные орграфы, отображающие преобразование элементами системы потоков теплоты ЭС. Вершины ТПГ отображают элементы (технологические операторы), которые изменяют тепловые расходы физических потоков, точки стыковки трубопроводов, источники и стоки теплоты ЭС. Дуги ТПГ соответствуют физическим потокам теплоты.
Следует подчеркнуть, что кроме внешних источников теплоты могут быть и внутренние (фиктивные), например тепловой эффект, вызванный экзотермической химической реакцией.
Матричное представление графов позволяет отобразить структурные особенности графов.

Топологический метод следует применять к каждому материальному потоковому графу и к тепловому потоковому графу.
Если уравнения для всех материальных и тепловых потоковых графов образуют совместно разомкнутую систему уравнений, то получают ациклический информационный граф системы уравнений балансов ЭС.
Если уравнения связей рассматриваемого потокового графа образуют совместно замкнутую систему уравнений, то получают циклический информационный граф системы уравнений балансов ЭС.
При решении задач расчета балансов ЭС, для которых справедливы системы линейных уравнений материальных и тепловых балансов, топологический метод позволяет разработать ациклический информационный граф системы уравнений балансов ЭС.
Для анализа сложных встречно-направленных ЭС следует обращаться к иной стратегии анализа. Алгоритм оптимального анализа сложной энергосберегающей системы, отображаемой многократным параметрическим потоковым графом, представляет собой упорядоченный по слоям вершин эквивалентный ациклический ППГ. Его получают из многоконтурного исходного графа в результате разрыва минимального множества особых дуг Q*. Это устанавливает порядок расчета математических моделей отдельных элементов ЭС, соответствующих вершинам параметрического потокового графа.
Необходимо в исходном ППГ определить множество особых дуг
![]() (8.5) с минимальной суммой параметричностей.
(8.5) с минимальной суммой параметричностей.
Для энергетических систем основным критерием эффективности обычно служит преобразование потоков энергии в системе, а также термодинамическая степень совершенства функционирования системы в целом и ее отдельных элементов. При таком подходе оптимальное решение определяется условием, что потери энергии в системе минимальные
![]() (8.6)
(8.6)
ОСНОВЫ ЭКСЕРГЕТИЧЕСКОГО МЕТОДА АНАЛИЗА ЭНЕРГОСБЕРЕГАЮЩИХ СИСТЕМ
Для энергетической оценки технических систем наиболее целесообразно обращаться к методу эксергетического анализа.
Эксергия представляет собой количество работы, которое может быть получено внешним приемником энергии при обратимом взаимодействии системы или потока энергии с окружающей средой до установления полного равновесия [4].
По определению работа служит мерой энергии. Тем не менее, работа не обязательно является необходимым конечным результатом, т.е. целью действия анализируемой системы или потока эксергии. Конечным результатом действия анализируемой системы кроме работы могут быть преобразования теплоты, холода, получение нужных параметров и т.д. В реальном процессе работа меньше уменьшения эксергии (в пределе работа может равняться нулю), так как часть эксергии не превращается в работу, а исчезает (вследствии диссипации энергии).
Между энергетическим и эксергетическим балансами имеется принципиальная разница. Энергетический баланс системы не отражает потери от необратимости процессов в анализируемой системе. Эти потери определяют эксергетическим анализом. При энергетическом анализе “потеря энергии” означает не потерю энергии вообще (энергия исчезать не может), а потерю ее для данной системы. Речь идет о невозможности или неэффективности использования энергии из-за ее состояния или параметров. В эксергетическом анализе имеется исчезновение эксергии, т.е. её уничтожение, связанное с диссипацией энергии. Эксергия подчиняется закону сохранения только в обратимых процессах. В реальных системах эксергия может частично или полностью исчезать. Очевидно, чем меньше потери эксергии при прочих равных условиях, тем более эффективный в энергетическом отношении процесс протекает в системе. Поэтому при сравнительном анализе нескольких вариантов изучаемой системы следует выбирать вариант, который обеспечивает получение максимальной эксергии, т.е. вариант с минимальными потерями эксергии.
В общем случае уравнение эксергетического баланса записывается следующим образом
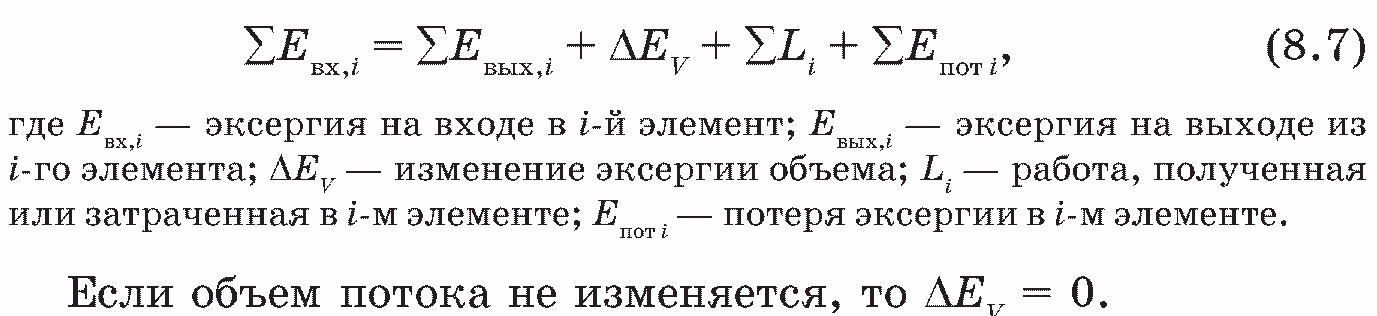
Отношение отводимой от системы эксергии £вых к подводимой эксергии Евх определяет значение эксергетического КПД
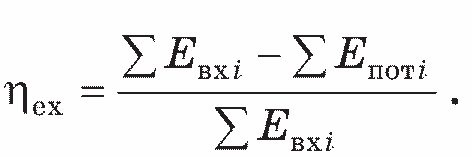
(8.8)
При построении эксергетического графа следует учитывать следующее. Процесс сжатия рабочего тела сопровождается возрастанием эксергии, а процесс расширения — ее уменьшением.
Эксергетический КПД реального процесса сжатия без отвода теплоты, но с внутренним трением, определяется по формуле


