§ 17—4. РАСЧЕТ ГРАВИТАЦИОННЫХ ПЛОТИН
Расчет гравитационных плотин должен подтвердить, что проектный профиль плотины статически устойчив, не имеет излишних запасов, что в нем напряжения не превосходят допускаемые, в основании плотины отсутствуют растягивающие напряжения, сжимающие находятся в допустимых пределах.
Рассмотрим элементарный профиль плотины — прямоугольный треугольник АВС (рис. 17 — 13), расположенный на горизонтальном основании АС и не испытывающий противодавления (коэффициент противодавления а = 0).
Плотина находится под воздействием двух сил: силы собственной тяжести![]() — объемная масса кладки, и давления воды, равна
— объемная масса кладки, и давления воды, равна



Учет строительных свойств основания (жесткости, упругости) на распределение в нем напряжений дает несколько отличные величины о, чем по уравнению 17—35; определение этого распределения напряжений ведется экспериментальным методом (метод тензосетки, оптический метод).
Кривая давлений не должна выходить из средней трети ширины горизонтальных сечений, т. е. нигде не должно быть растягивающих напряжений. Растягивающие напряжения у напорной грани плотины могут вызвать появление трещин или раскрытие горизонтальных швов, что повлечет за собой перераспределение сил и напряжений в сторону ухудшения прочности и устойчивости плотины.
Лишь в верхней части плотины при учете значительного давления льда можно допустить растягивающие напряжения, для восприятия которых по напорной грани ставят арматуру.
Получающиеся по расчету большие скалывающие напряжения, превосходящие обычно допускаемые, не ведут к разрушению плотины, что объясняется условиями работы бетона (только сжатие), повышающими сопротивление его скалыванию.
Прочность гравитационных плотин определяется величиной нормальных (сжимающих) напряжений.
§ 17—5. РАСЧЕТ УСТОЙЧИВОСТИ ГРАВИТАЦИОННЫХ ПЛОТИН
Устойчивость гравитационных плотин против опрокидывания вокруг низовой бровки (вокруг точки С на рис. 17—13) всегда обеспечена, если равнодействующая сил не выходит за границу очертания основания плотины, т. е. и тогда, когда равнодействующая выходит из ядра сечения и когда по подошве плотины могут быть растягивающие напряжения.
Устойчивость плотин па сдвиг по горизонтальной подошве будет обеспечена, если сдвигающие силы будут меньше сил сопротивления сдвигу. Сдвигающие силы могут быть определены достаточно точно; что же касается определения сил сопротивления, то здесь нет такой ясности.
Если считать, что по всей подошве плотины сцепление бетона плотины со скалой обеспечено, то тогда коэффициент устойчивости на сдвиг найдется из уравнения: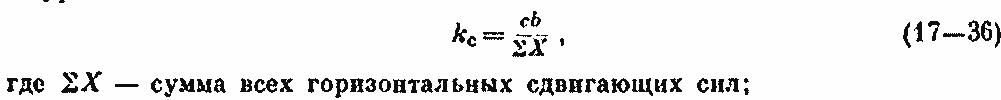
с — удельное сцепление бетона плотины с основанием;
b — ширина основания плотины.
Рассмотрим устойчивость плотины, у которой подошва не горизонтальна, а обработана в форме зубцов (рис. 17—1).
В том случае, когда временное скалывающее напряжение скалы меньше с, скалывающее усилие по зубцам скалы будет иметь меньшую величину, чем усилие сцепления скалы с бетоном плотины, и в формулу (17—36) вместо с следует подставлять временное скалывающее напряжение скалы; так же поступают, когда временные скалывающие напряжения бетона меньше с (более редкий случай).
Устройство армированного зуба (рис. 17—11) значительно повышает устойчивость плотины на сдвиг.

