Гидротехнические сооружения - Расчет флютбетов по методу гидродинамики

3-3. РАСЧЕТ ФЛЮТБЕТОВ ПО МЕТОДУ ГИДРОДИНАМИКИ
В создании и развитии теории гидродинамики выдающееся значение имеют труды великого русского ученого Николая Егоровича Жуковского. Классические работы Н. Е. Буковского по гидродинамике грунтовых вод (1890 г.), теоретическое исследование о движении подпочвенных вод (1889г.), о влиянии давления на насыщение водой песка (1890 г.), о просачивании воды через плотины (1920 г.) и др. нашли применение только в советское время.
Профессором А. А. Адамовым в Петербургском политехническом институте читался курс «Уравнения математической физики», в котором рассматривался случай гидродинамического решения движения грунтовых вод под плоским флютбетом и обтекания вертикального шпунта (издан литографически в 1909 г.). Акад. Η. Н. Павловским в 1922 г. издан классический труд «Теория движения грунтовых вод под гидротехническими сооружениями». Проф. А. Ф. Лебедевым опубликована замечательная работа «Почвоведение и грунтовые воды». Труды упомянутых русских ученых не имели и нс имеют себе равных за границей. Отечественная советская наука о движении грунтовых вод идет впереди науки капиталистических стран Европы и США. Как в вопросах теории, так и при решении практических задач советской науке о движении и физике грунтовых вод принадлежит ведущее место.

¹ Установление факта неравномерности гашения напора вдоль флютбета неправильно приписывалось Е. Лену (1934 г.), к тому же ошибочно принявшему ее постоянной. При сильно развитых горизонтальных и слабых вертикальных путях эффективность горизонтальных путей больше эффективности вертикальных.

Теория струйного движения грунтовой гравитационной воды не ограничивается рассмотрением движения только одной струйки по стыку флютбета с грунтом основания (как это было показано выше), а изучает движение по всей области проницаемого грунта.
Движение рассматривается установившееся и плоское, т. е. изменяющееся вдоль флютбета (по длине х) и в глубь грунта (по глубине у); в направлении же, перпендикулярном продольной оси сооружения (т. о. по третьей координате z), считают, что движения нет. Кроме того, проницаемому грунту основания приписываются, по Η. II. Павловскому, следующие свойства.

1. Считают, что грунт по всей области однороден по своим фильтрационным свойствам (одинаков но механическому составу и порозности).
2. Движение воды но порам грунта различают двух видов: местное, когда обтекаются отдельные частицы грунта, и главное, характерное для общего направления и интенсивности потока.
3. Элементарные струйки воды, образуя главное течение, непрерывны; извилистость этих струек вследствие местных течений не нарушает непрерывности главного течения, поэтому извилистостью струек в теоретических подсчетах пренебрегают, учитывая ее (не явно) в величине коэффициента фильтрации.

Перечисленные свойства грунта возможны, попятно, лишь при наличии достаточно больших размеров области потока по сравнению с величиной отдельных зерен грунта.
При выполнении перечисленных условий по теории струйного движения можно подсчитать для любой точки проницаемого грунта скорость движения и пьезометрическое давление потока в ней и, как следствие, распределение давлений потока вдоль флютбета, скорости выхода воды через дно нижнего бьефа и по ним потери воды на фильтрацию. Зная давление на флютбет, можно определить его толщину, проверить по допускаемым выходным скоростям потока длину флютбета.
Для выяснения элементов потока грунтовых вод применяют уравнения Дарси в дифференциальной форме:
(3-4)
где h — напор в точке с координатами х, y, z, измеряемый от некоторой произвольно выбираемой горизонтальной плоскости сравнения;
к — коэффициент фильтрации грунта;
и, v, w — компоненты скоростей по направлению осей в точке с координатами х, у, z.
Уравнение неразрывности для такого движения обладает рядом интересных свойств: оно получается из условия равенства объемов втекающей и вытекающей воды из любой замкнутой фигуры в области движения.

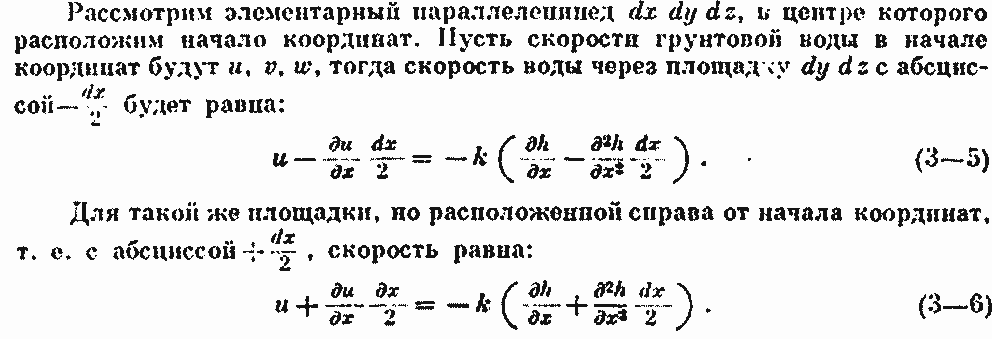
Разность скоростей, умноженная на живое сечение dy dz, должна дать разность между объемами притекающей и уходящей воды из элементарного параллелепипеда по направлению оси ОХ, т. е.:

(3-7)
Составляя подобные уравнения для двух остальных осей (ΟΥ и ΟΖ) и складывая их с предыдущим, получаем разность объемов воды, поступившей и ушедшей из параллелепипеда, а так как эта разность для установившегося движения жидкости постоянной плотности равна нулю, то в результате получаем уравнение Лапласа:
(3-8)
Рассматривая h как потенциальную функцию напоров, видим, что уравнение (3—8) аналогично уравнению стационарного распределения тепла в изотропной среде; оно также аналогично стационарному распределению электрического потенциала и магнитных масс в изотропной среде; следовательно, свойства изотермических кривых возможно распространить и на движение грунтовых вод.
Изотермические кривые, линии равного потенциала (эквипотенциальные), т. с. линии равных температур или потенциала, перпендикулярны линиям токов, т. е. линиям перемещения тепла, электричества; следовательно, и в потоке грунтовых вод линии равных напоров (аналогичные изотермам) будут направлены перпендикулярно к линиям течения воды.
Таким образом, движение грунтовых вод, следующее закону Дарси, может быть изображено ортогональной сеткой кривых: линиями равных напоров и их изогональными траекториями — линиями течения воды. Перпендикулярность потенциалей и траекторий может быть установлена из таких простых соображений. Допустим, что скорость в какой-либо точке потенциали направлена наклонно к ней. тогда можно будет разложить скорость на две составляющие — на нормальную к потенциали и вдоль потенциали.
Так как на потенциали везде напор постоянен, то вдоль нее отсутствует причина, возбуждающая движение, и, следовательно, вдоль потенциали скорость будет равна нулю. Отсюда получаем ортогональность потенциалей и траекторий. Следовательно, движение грунтовых вод совпадает с движением идеальной жидкости при соблюдении тех же условий ортогональности линий на контуре (за исключением особенных точек); для практики, когда скорости движения меньше критических и движение следует закону Дарси, выводы, получаемые из уравнения Лапласа, вполне приемлемы.
Для расчета движения грунтовых вод, т. е. для выявления полной картины движения (скоростей, давлений, расходов в любой точке области потока), необходимо и достаточно получить решение уравнения Лапласа (3—8) в условиях заданных значений потенциальной функции на контуре области потока.
Непосредственное решение уравнения Лапласа сложно, несколько проще решение получается в случае применения способа конформных изображений или векторного анализа. Не останавливаясь здесь на аналитическом решении, укажем на капитальный труд по этому вопросу акад. Н. Н. Павловского «Теория движения грунтовых вод под гидротехническими сооружениями». Более просто решение получается графически; оно может быть получено также на приборе, предложенном акад. И. Н. Павловским и основанном па методе электрогидродинамических аналогий — ЭГДА.
Графическое решение, очевидно, будет заключаться в получении такой наглядной картины движения, пользуясь которой можно будет указать для любой точки потока его элементы.
Такой картиной является так называемая гидродинамическая сетка, или, кратко, сетка движения, т. е. изображение направления элементарных струек воды (траектории движения) и линий, вдоль которых напоры везде одинаковы.

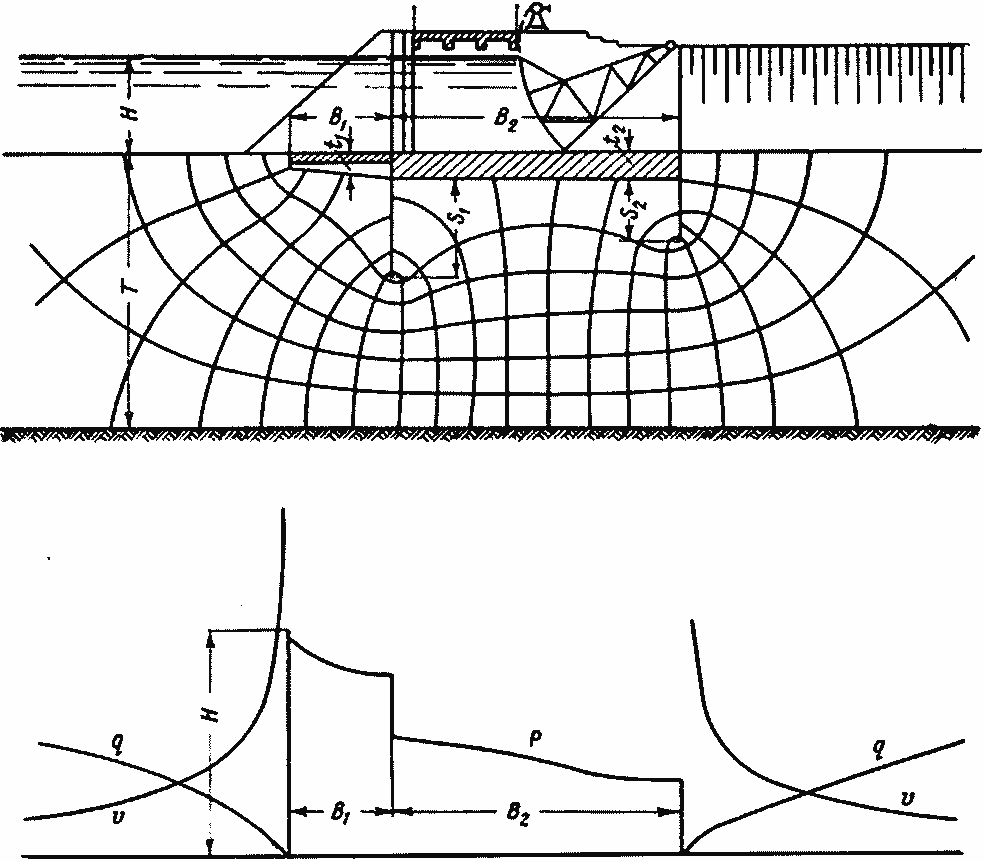
Рис. 3—5. Гидродинамическая сетка для двух шпунтового флютбета, эпюры напоров р скоростей фильтрации и суммарных расходов на фильтрацию q.

Пример графического построения сетки движения приведен па рисунке 3—5, где показаны линии течения (траектории струек) под двухшпунтовым флютбетом и линии равных напоров. Назовем пространство, ограниченное двумя соседними линиями равных напоров (т. е. потенциальными линиями), поясом давлений. Здесь число поясов давлений П = 19, причем построение выполнено так, что при переходе от одной потенциальной линии к другой напор изменяется на, где Н —- действующим напор, равный Н = Н1 — Н2. Так, например, вдоль первой эквипотенциали напор везде равен Н, (принимая за плоскость сравнения дно канала); вдоль последней потенциал и напор везде равен Н2; во внутреннем углу за первым шпунтом, до которого от дна нижнего бьефа имеется примерно 9.7 пояса давлений, напор будет равен
•
Таким образом, семейство эквипотенциален позволяет найти напор, а по нему и давление в любой точке потока, следовательно, и вдоль флютбета.
Назовем пространство, ограниченное двумя соседними траекториями, лентой расхода. На рисунке 3—5 число лент расхода Л = 6, причем они так построены, что в каждой ленте протекает один и тот же расход. Отсюда очевидно, что общий расход па фильтрацию будет равен шести элементарным расходам.

Каким условиям должна удовлетворять сетка движения, чтобы в ней через каждую ленту протекал одинаковый расход и чтобы так терялась одна и та же доля напора? Таких условий существует три: 1) пересечения траекторий и потенциален должны быть нормальны между собой; 2) сетка должна быть составлена из подобных прямоугольников, лучшая форма для таких прямоугольников — квадрат; 3) сетка должна быть непрерывной и заполняющей всю область фильтрации.
Графическое построение сетки движения производится таким образом. Как дно верхнего, так и дно нижнего бьефов являются начальной и конечной потенциалями сетки, поэтому линии тока должны быть им нормальны; далее, так как подземное очертание водонепроницаемых частей флютбета и очертание поверхности водоупора являются первой и последней линиями токов сетки, то потенциал и должны быть им перпендикулярны.
Сетку начинают строить с первой ленты; для этого от начала понура и до рисбермы строят непрерывный ряд криволинейных квадратов, из которых квадраты во внутренних углах флютбета (в углах меньших 180о) превратятся в пятиугольники, во внешних углах флютбета (в углах, больших 180°, например у конца шпунта угол равен 360°) — в треугольники. Построив первую ленту, таким же образом строят вторую, добиваясь выполнения указанных выше трех условий.
При некотором навыке сетки строятся достаточно быстро п точно. Квадратичная форма ячеек сетки наиболее проста в исполнении и наиболее легко контролируема по точности. Криволинейные квадраты обладают рядом свойств, присущих и прямолинейным квадратам: так, у криволинейных квадратов все углы прямые, криволинейные серединные линии равны между собой; равны между собой и криволинейные диагонали. Гидродинамическая сетка является результатом решения уравнения Лапласа методом конформных отображений и, как следствие этого решения, доли погашаемого напора при переходе от любой потенциали к соседней оказываются постоянными и равными Н/П; также оказываются одинаковыми расходы на фильтрацию в каждой ленте.
Гидродинамические сетки, тщательно выполненные графическим путем, дают ту же точность, что п построенные аналитически; сетки, выполненные графическим путем менее тщательно, дают отклонение от аналитического решения около 5%.
Проделав несколько таких приближений, добиваются плавного очертания всех линий, образующих прямоугольную сетку, и совпадения нижней липни тока с поверхностью водоупора; при этом нет необходимости добиваться целого числа лент и поясов.
В теории конформных отображений доказывается, что для заданных очертании флютбета и области проницаемого грунта может быть построена, независимо от коэффициента фильтрации грунта основания, только одна сетка (единственность решения уравнения Лапласа для заданных условий), т. е. отношение для нее (так называемый модуль сетки) будет величиной постоянной.
Любую редкую сетку можно сделать более подробной, проведя в ней дополнительные средние линии токов и потенциален, не изменяя величины модуля сетки. Отметим, что проведение средних линий токов и потенциалей является хорошим средством проверки точности построения сетки.
Построив сетку из криволинейных квадратов, можно по ней определить все элементы потока грунтовых вод. Так, расход воды на фильтрацию под флютбетом будет:
(3-9)
где к — коэффициент фильтрации грунта основания;
Н = Н1 — Н2 — действующий напор;
В — ширина флютбета;

Π — число поясов давлений сетки:
Л — число лент расхода сетки;
Формула (3—9) выведена из следующих соображений.

Если сетка нс квадратичная, а составлена из криволинейных прямоугольников, подобных вследствие конформности их построения, то здесь отношение ∆s к ∆l также постоянно для всей сетки, по не равно единице, как это мы имели для квадратичной сетки.
Отношение ∆s : ∆l называют коэффициентом формы сетки.
Из уравнения (3—11) видно, что расход одной любой ленты будет величиной постоянной.
Относительно определений напоров потока по сетке выше были сделаны пояснения. Укажем здесь на следующее свойство сетки: если бы сквозь кладку флютбета провести пьезометрические трубки в грунт и окончить их все на одном какой-нибудь эквипотенциали, то во всех трубках вода стояла бы па одном уровне. Например, пусть концы трубок будут располагаться в разных точках потенциали, разделяющей 16-й и 17-й пояса, считая от конца водобоя, тогда во всех трубках высота воды будет равна Н2 + 16/19 х Н (рис. 3—5).
По сетке движения можно определить и скорости движения; выше, при определении расхода, мы имели для какого-нибудь квадрата скорость, равную (при прежних обозначениях):
(3-13)
Таким образом, гидродинамическая сетка дает возможность найти все интересующие нас элементы потока грунтовых вод: так, на рисунке 3—5 показаны: кривая давлений на флютбет Р. кривые входных и выходных скоростей фильтрации v вдоль дна верхнего и дна нижнего бьефов, кривые суммарных удельных расходов Σq через дно верхнего и нижнего бьефов.
В тех случаях, когда слой проницаемого грунта Т очень глубок, примерно около длины L — для плоского флютбета и около (1,25—1,5) L — для флютбета одношунтового (т. е. Т = 1,5 L), построение сетки несколько изменяется. Теоретические выкладки и результаты опытов ¹ показывают, что интенсивность движения грунтовых вод по мере удаления от флютбета в глубь грунта быстро затухает и примерно на указанных глубинах движение настолько слабо, что для слоев грунта, еще более низко расположенных, можно этим движением пренебречь. Далее, из теории струйного движения известно, что если мы примем любую из траекторий движения (т. t. линии течений, линий тока) за новую границу области движения, то от этого оно не изменится. Последнее обстоятельство, в связи с затуханием движения по мере понижения в грунт, в применении к построению сеток движения для случаев очень мощных слоев проницаемого грунта используют следующим образом: мы ограничиваем рассмотрение движения активной зоной с глубиной Т = L или 1,25L, задаемся формой пограничном линии течения — для плоских флютбетов эллипсом.
В случае шпунтовых флютбетов за очертание активной зоны принимается плавная кривая, проходящая через точки дна канала, отстоящие от концов непроницаемых частей флютбета (понура и водобоя) на (0,8-1) L и через точку, расположенную на (14-1,5) по вертикали от нижнего конца шпунта длиной S.
Согласно струйной теории, давления воды на флютбет распределяются по кривым, не зависящим от фильтрационных свойств однородного грунта (т. е. от коэффициента к) и далеко отклоняющимся от прямой, построенной по методу линейной контурной фильтрации; в большинстве случаев криволинейное распределение указывает на меньшие давления в верхней части флютбета и большие — в нижней, по сравнению с прямолинейным распределением.
Такое распределение давлений позволяет делать флютбеты меньшей толщины в начале, не всегда увеличивая ее в конце, где толщина определяется не расчетом, а чаще конструктивным минимумом. Аналитическое и графическое решения дают возможность построения эпюр скоростей входа и выхода воды по дну каналов, давлений вдоль подошвы флютбета и построения изотах но области движения.
Вследствие принятого метода решения (конформное преобразование) и очертания флютбета (составленного из прямых линий с резкими углами поворотов) в местах поворотов контура флютбета (например, под шпунтами и зубьями) получаются теоретически бесконечно большие скорости фильтрации.
Акад. Н. Н. Павловский считает, что для зоны вокруг точек с такими теоретическими скоростями ламинарное движение нарушается.
Такие точки, в действительности небольшие области с сосредоточением относительно больших скоростей течения, называются фокусами; для устойчивости грунта они не представляют опасности, кроме тех из них, за которыми вода выходит в нижний бьеф, создавая угрозу выноса частиц грунта (так называемые фокусы размыва).
Для нейтрализации влияния низового фокуса размыва необходимо устройство в конце флютбета зуба или шпунта такой глубины, на которой скорости фильтрация могли бы выровняться и уменьшиться у дна нижнего бьефа до величин, не угрожающих вымыву грунта. На рисунке 3—6 показано влияние концевого шпунта на уменьшение выходных скоростей потока грунтовых вод.
Полезно для усиления устойчивости грунта укреплять его обратными фильтрами (см. рис. 3—19).

¹ Е. А. 3амарин. Движение грунтовых вод под гидротехническими сооружениями. Ташкент, 1928. Активная зона грунта, по опытам, оказалась равной около 0,5— 0,75 L, считая по дну канала в обе стороны от флютбета. В опытах со сквозными флютбетами она оказалась равной 0,75—1,0 L (см. Е. А. Замарин. Расчет сквозных флютбетов. Ташкент. 1932); А. М. Сенков и Н. Ф. Фильчаков. Приближенные методы расчета стационарного движения грунтовых вод под гидротехническими сооружениями. Изд. Академии наук Украинской ССР, Киев, 1952.

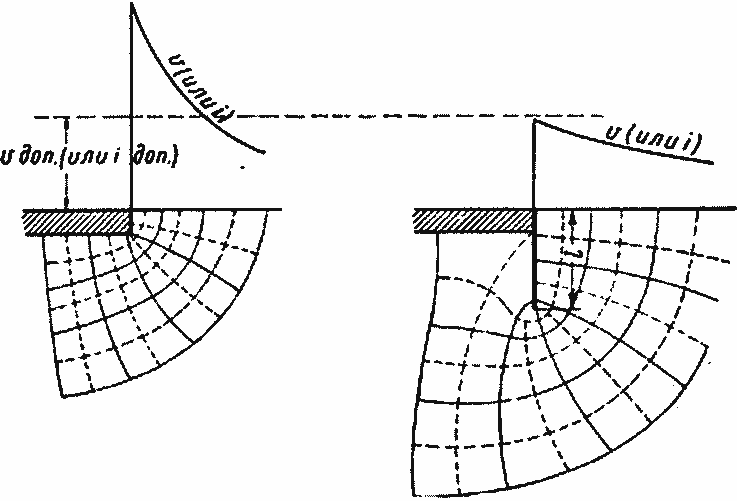
Рас. 3—6. Выходные скорости фильтрационного потока за плоским флютбетом и за шпунтовым флютбетом.

Аналитическое решение уравнения Лапласа позволяет составить номограммы для определения давления фильтрационного потока на флютбет. Ниже приводится несколько номограмм и абак, дающих обобщенные решения, т. е. удельные давления hr фильтрационного потока на флютбет для

Рис. 3—7. График удельных давлений на плоский заглубленный флютбет.
Находим горизонталь через точку t : b = 0,2 и получаем следующее распределение давлений фильтрационного потока по подошве флютбетов относительно плоскости сравнения, проходящей по уровню нижнего бьефа (табл. 3—3).
Таблица 3-3

1. Плоский флютбет, расположенный на водопроницаемом грунте слоем Т. Для отыскания удельных давлений на флютбет построен график (рис. 3—8), пользование которым аналогично предыдущему: находят отношение полудлины флютбета b к глубине Т (или L к 2); соответственно найденному отношению проводят горизонталь, пересечения которой с помеченными линиями удельных давлений укажут приведенные абсциссы точек и удельные давления в них. Как видно из графика, начиная с L = Т, распределение удельных давлений по флютбету мало отличается от распределения соответствующего t — ∞ (нижняя горизонтальная линия).
2. Плоский одношпунтовый флютбет, расположенный на мощном водопроницаемом слое грунта. Выбирается следующая координатная система: положительная ось ОХ направлена по горизонтальной подошве флютбета в сторону нижнего бьефа, ось ОУ — вниз по вертикальному шпунту; за единицу масштаба принимается длина шпунта, т. е. s=1.

Таблица 3—4

Рис. 3—8. График удельных давлении для плоского заглубленного флютбета на проницаемом слое конечной глубины.

На рисунке 3—10 показана система координат и приведена эпюра распределения удельных давлений по флютбету, подсчитанная по номограмме (сплошные кривые линии); там же показана эпюра удельных давлении, построенная по способу линейной контурной фильтрации (прямые пунктирные линии), которая значительно отличается от номографической.

Таблица 3—5

Рис. 3—9. Номограмма удельных давлений для одношпунтового флютбета.

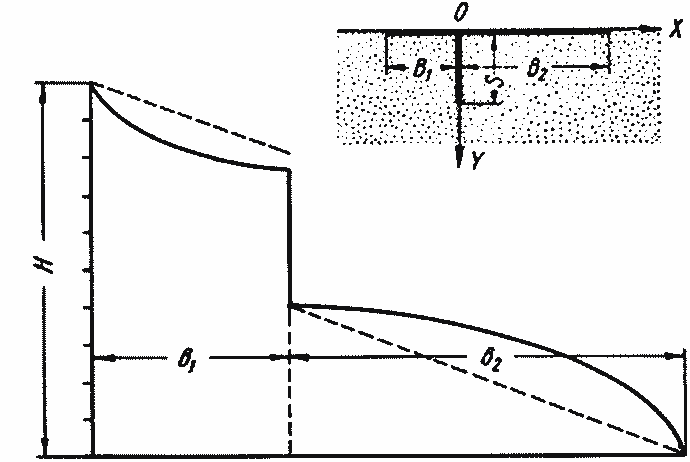
Рис. 3—10. График удельных давлении на одношпунтовый флютбет.

Фильтрационное давление на подземный контур сооружения при наличии двух, трех и более шпунтов может быть определено приближенным гидромеханическим расчетом по методу коэффициентов сопротивления, разработанному Р. Р. Чугаевым¹. 

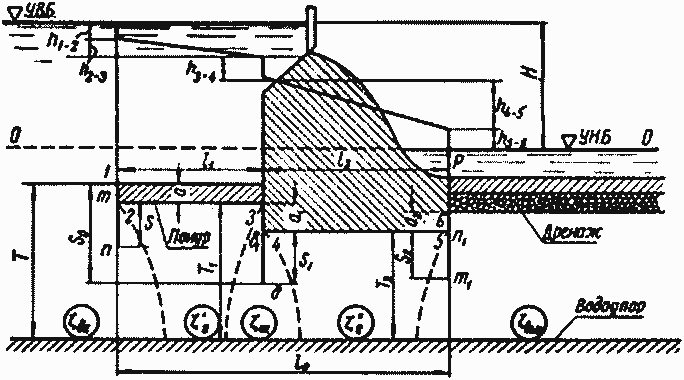
Рис. 3—11. Схема разбивки подземного контура плотины на участки (по Р. Р. Чугаеву).

Подземный контур предварительно делится на отдельные вертикальные и горизонтальные участки (элементы), как показано на рисунке 3—11. Практически все участки можно привести только к трем типовым элементам:

1. входной или выходной элемент в общем случае имеет вид входного и выходного шпунта 1 — п — 2 и 5 — т1 — 6, а при отсутствии шпунта представляет уступ 1 — т = а и — 6 = а2;

Суммарный коэффициент сопротивления:

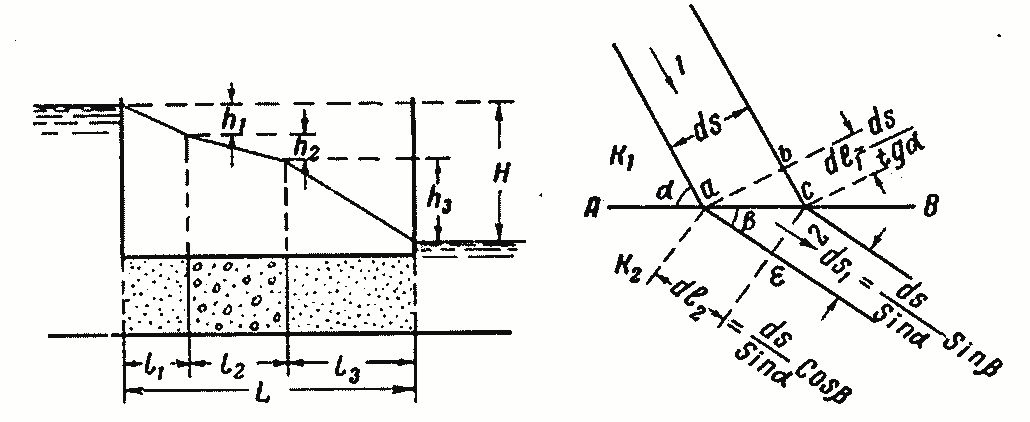
Рис. 3—12. Напорный поток в разнородных грунтах.
Рис. 3—13. Излом линий на стыке разнородных грунтов.