4-5. Методика выравнивания ресурсов по дням ремонта со свободным обменом ресурсами
Задача выравнивания ресурсов сводится к такому распределению по времени работ, входящих в состав сетевого графика в пределах их резервов, чтобы суммарное количество рабочих, ежедневно выполняющих эти работы, было стабильным. Иными словами, надо составить рациональное расписание работ так, чтобы
n=f(t) — const.
Эта задача относится к выравниванию числа рабочих одной специальности, занятых на однородных работах, когда каждую из входящих в график работ могут выполнять любые рабочие из состава бригады. Следовательно, выравнивание числа рабочих применимо к бригаде, выполняющей ремонт узла агрегата, или к нескольким бригадам одной организации, выполняющим ремонт ряда однородных узлов.
Такая задача может быть названа оптимизацией без ограничения в обмене ресурсами, но стабильность в составе каждой отдельной бригады не может быть обеспечена, так как достигается стабильность общего числа рабочих, входящих во все совместно оптимизируемые бригады, причем перемещение рабочих из одной бригады в другую не ограничивается. Совершенно ясно, что совместно нельзя оптимизировать два графика, если каждый из них выполняется рабочими различной специальности или различных организаций.
В действительности даже в пределах одного узла работы не одинаковы по своей сложности, и поэтому их предстоит выполнять рабочим разной квалификации. Однако распределение по работам — задача бригадира, и она не должна решаться при оптимизации ресурсов. Практически целесообразно применять метод группировки, согласно которому предстоит иметь дело с составом бригады условно одинаковой квалификации со средним разрядом, соответствующим сложности ремонта поручаемых бригаде узлов. При этом, если в состав бригады включаются рабочие других профессий, например сварщики, а их полная загрузка в течение всего периода ремонта узла при совместной работе с бригадой очевидна и обоснованна, эти специальности могут не выделяться отдельно и учитываются при оптимизации ресурсов наравне с другими рабочими бригады.
Задача выравнивания ресурсов становится практически доступной для решения при следующих условиях:
а) плотность используемого на работе ресурса остается неизменной на протяжении всей работы. Если же предусматривается, что на работе i, j количество рабочих будет вначале n1, а затем п2 (состав звена будет уменьшен или увеличен), то эта работа должна быть разбита на две работы i, k с длительностью t(i,k) и ресурсом п2 и k, j с длительностью t и ресурсом п2;
б) начало или окончание каждой работы может осуществляться только на границе двух единиц времени, принятых для данного сетевого графика, но не в пределах этой единицы (см. § 3-5).
При соблюдении указанных условий график n = f(t) будет всегда иметь ступенчатый характер с минимальной длиной ступеньки, равной единице времени (смена, сутки). Критерием оптимальности в задаче выравнивания числа рабочих является его равномерность по дням ремонта, которая хорошо характеризуется среднеквадратичным отклонением ежедневно занятого на ремонте числа рабочих от среднего ежедневного их числа за время Т.
Целью оптимизации является минимизация этого отклонения. С учетом условий, указанных выше, при ступенчатом характере зависимости n=f(t) минимизируемая функция будет иметь вид:
![]()
На рис. 4-7 показана зависимость n=f(t) для трех случаев организации работ с одинаковой длительностью Т=4 дня. Для всех трех ступенчатых характеристик среднее количество работающих также одинаково: пср= 4. Значение минимизируемой функции равно:
Для 1-й характеристики φ=4 · 42 = 64;
для 2-й характеристики φ<=2 · 52 + 2 · 32=68;
для 3-й характеристики φ= 2 · 62+2 · 22 = 80.
Для условий данного примера при φ>=64 обеспечивается полное выравнивание кривой. С возрастанием φ увеличивается неравномерность использования рабочих по дням выполнения работы.
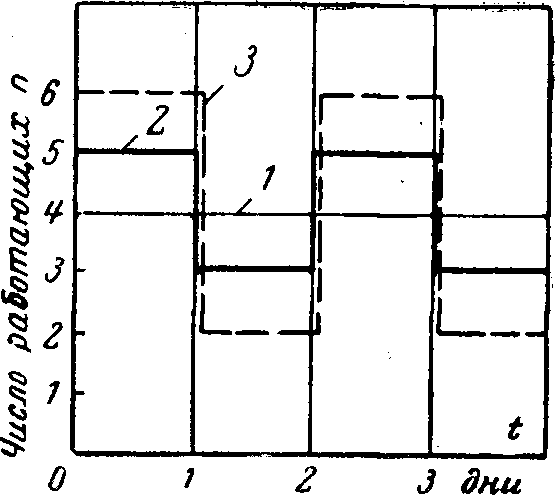
Рис. 4-7. Пример различной формы характеристики изменения числа работающих по дням выполнения работы.
Задача выравнивания ресурсов относится к комбинаторному типу задач, не имеющих строгого аналитического решения. В [Л. 5] предложен алгоритм для выравнивания ресурса, обеспечивающий практически удовлетворительное решение задачи при значительно меньших затратах времени, чем при использовании перебора вариантов, в связи с направленным и организованным порядком действий.
Допустим, имеется работа k, l продолжительностью t дней. Условимся отмечать первый день работы i, а последний j. В этом случае в продолжительность t входят дни i, (i + 1), (i + 2) ... (i + m—2), j, где т — продолжительность работы в днях. Количество рабочих, занятых на работе k, l, обозначим n. Суммарное количество рабочих, занятых на всех работах оптимизируемого графика, — N. В дни, когда выполняется работа k, l, -N приобретает значения Ni, N(i+1)... Nj.
Чтобы установить, будет ли увеличиваться или уменьшаться минимизируемая функция φ при перемещении работы k, l на один день вправо, т. е. когда ее первым днем вместо i будет день i + 1, а последним днем будет не j, а j+1, необходимо вычислить величину
![]()
- (4-1)
При![]() (отрицательное значение) φ уменьшится;
(отрицательное значение) φ уменьшится;
следовательно, сдвиг работы на один день вправо, если это разрешает ее резерв времени, целесообразен.
При ΔN=0 φ не изменится; следовательно, сдвиг работы нецелесообразен.
При ∆Ν>0 (положительное значение) φ увеличится, следовательно, сдвиг работы на один день вправо нецелесообразен.
В случае, когда ∆Ν<0, работа сдвигается на один день вправо, корректируются в соответствии с этим ресурсы дней i— (N'i=Ni—пk, l) и j+1—(N'j+l=Nj+i + nk,l) и исследуется целесообразность последующего перемещения работы на один день вправо тем же способом. При этом первый день работы вновь отмечается как день i (как будто бы первого передвижения вовсе не было).
В случае, когда ∆Ν>0 и сдвиг работы на один день вправо нецелесообразен, необходимо выяснить целесообразность сдвига работы сразу на два, затем на три и больше дней, вплоть до исчерпания ее резерва. Такой сдвиг будет целесообразен в том случае, если на пути передвижения работы по оси времени вправо окажется пик суммарного числа рабочих N, за которым располагается впадина, в пределах которой можно расположить передвигаемую работу k, l. Поэтому, зафиксировав величину ∆N при ее положительном значении
![]()
определяют![]() и затем
и затем ![]()
Такие исследования выполняются и дальше вплоть до полного исчерпания резерва времени работы k, l.
Следует иметь в виду, что при наступлении такого очередного этапа вычисления ∆N, когда предстоит сравнить ресурсы в дни i+m+l и i+m, вычисляют разность
ΔN=Nj+m+1—Nj-i, так как i + m — j+i и ресурс работы k, l в состав ресурсов этого дня не входит. Аналогично производится расчет и в последующие дни.
Для подсчета суммарной ежедневной потребности рабочих и анализа целесообразности перемещения работ по времени и их последующего сдвига строится упрощенная масштабная линейная диаграмма сетевого графика, область использования которой ограничивается решением задачи выравнивания числа рабочих но дням ремонта. Более подробно способ построения линейной диаграммы описан ниже.
Следует иметь в виду, что по выполнении первого шага оптимизации и исследовании целесообразности перемещения всех работ, имеющих резервы времени, и соответствующего их сдвига, следует произвести аналогичный второй, а может быть и третий шаг, каждый из которых улучшит достигнутое на предыдущем шаге качество выравнивания.
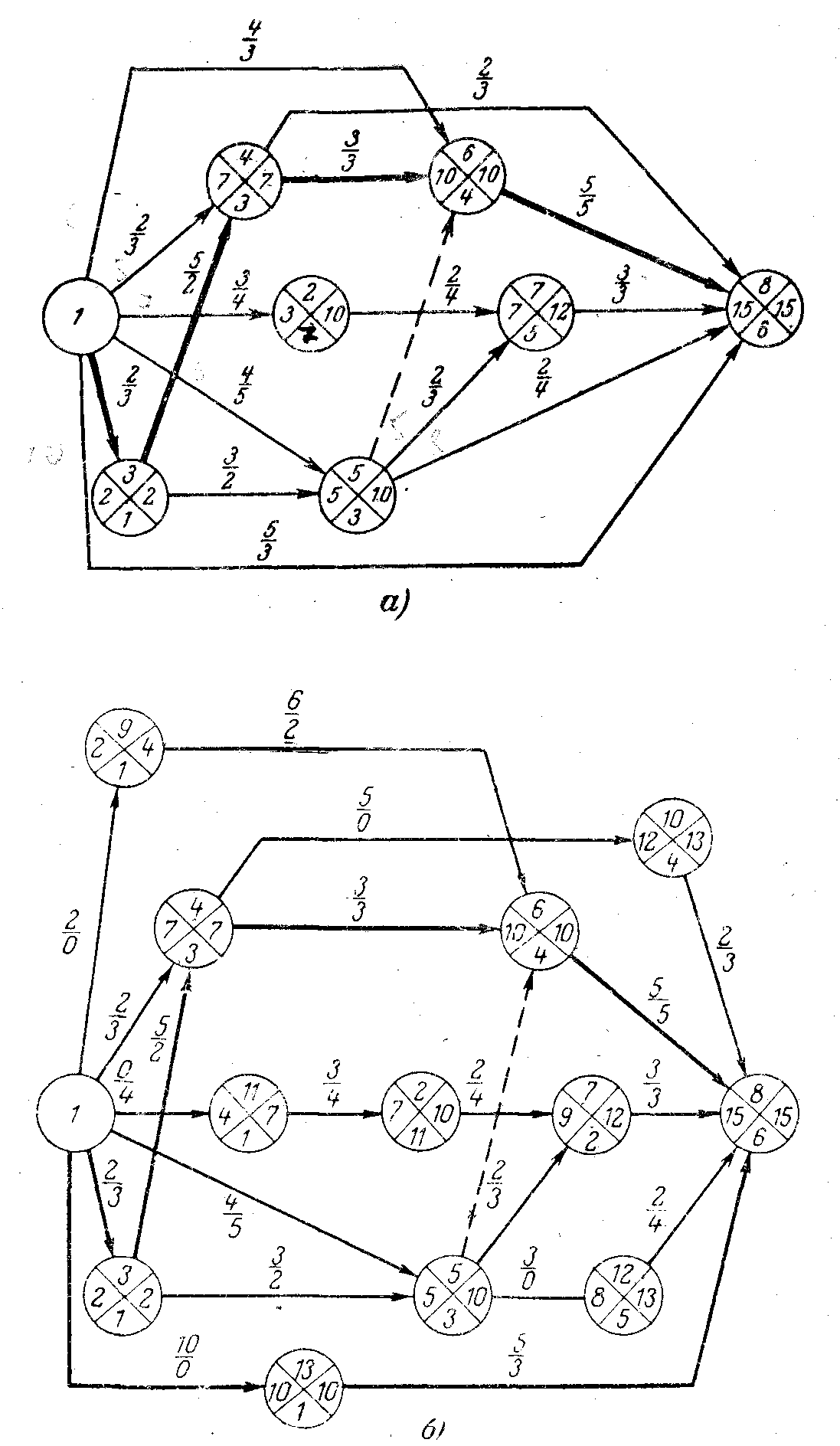
Рис. 4-8. Сетевой график.
а — до оптимизации ресурсов; б — после оптимизации ресурсов.

