Глава 6
ВОЗМОЖНЫЕ ВОЗДЕЙСТВИЯ ЭНЕРГЕТИЧЕСКОГО ОБЪЕКТА
В этой главе рассматриваются способы сопоставления возможна площадок с учетом поставленных целей. Положим, возможные площадки Sj, где j= 1,..., J, идентифицируются так же, как иерарх целей с критериями Хi (где i = 1, ..., n), построенная по принципу понижения уровня цели. В этом случае последствия размещения энергетического объекта на площадке Sj должны описываться вектором х (j) = (j), .... хп (j)), где xi (j) — уровни критерия Xi для площадки Sj.
Если отсутствует неопределенность, т. е. известны воздействия да всех площадок, выбор площадки сводится к выбору лучшего значения x(j). Сначала, однако, должны быть определены значения для каждой площадки и критерия. В данной главе рассматривается определение этих значений.
На практике, однако, чаще оказывается невозможным точно оценить последствия воздействий, так как из-за недостатка информации или чрезмерной стоимости ее получения воздействие энергетически) объектов на окружающую среду бывает известно неточно. Неопределенность в оценке как стихийных событий (например, землетрясений), так и аварий, вызванных деятельностью человека, влечет за собой неопределенность в оценке влияний энергетических объектов на здоровье и безопасность людей. Сложность социальных процессов приводит к неопределенности в оценке социально-экономических воздействий и воздействий на общественное мнение. Оценки же затрат, как известно, сильно зависят от степени детерминированности оценок. Можно описать эту неопределенность оценок, используя вероятностные методы. Каждая площадка Sj характеризуется несколькими возможными последствиями Xj и их вероятностями. Формализованно возможное воздействие на площадки Sj определяется распределением вероятности рj (х), j = 1, ...., J.
Как подчеркивалось в § 1.4, учет временного фактора, часто осуществляемый при анализе размещения энергетических объектов, усложняет описание возможных воздействий. Это происходит по двум причинам. во-первых, одно и то же воздействие, происходящее в различные
периоды времени, необязательно оценивается одинаково. Это можно пояснить на примере денежных затрат: 1 млн. долл, сегодня не тоже самое, что 1 млн. долл, через 10 лет. Во-вторых, неопределенность в оценке воздействий для отдаленного будущего обычно больше, чем для близкого. Вследствие этого желательно иметь распределение вероятности, описывающее возможные воздействия во времени.
Построение главы. В § 6.1 описываются методы количественной оценки воздействий для отдельных площадок. В основном глава посвящена иллюстрации этих методов. Параграфы 6.2—6.6 касаются воздействий соответственно на окружающую среду, экономику, социальную экономику, здоровье и безопасность людей и, наконец, общественное мнение. В § 6.7 и 6.8 более подробно рассмотрено применение методов, изложенных в § 6.1, касающихся наиболее важных проблем, не поддающихся общему формализованному описанию.
МЕТОДЫ КОЛИЧЕСТВЕННОЙ ОЦЕНКИ ВОЗДЕЙСТВИЙ
По существу имеются три различных подхода, используемых для описания возможных воздействий энергетического объекта:
сбор и анализ данных;
моделирование процессов, вызывающих воздействия;
прямая экспертная оценка.
Часто используются их комбинации. Для наглядности каждый подход будет рассмотрен отдельно. Но приводятся примеры и комбинированного их использования. Обсуждаются методические и практические результаты рассматриваемых подходов.
Сбор и анализ данных
Иногда отсутствие или очень незначительная степень неопределенности в оценке какого-либо воздействия энергетического объекта позволяет сразу выбрать площадку Sj. Так было, например, при исследовании по размещению АЭС компании WPPSS, рассмотренном в гл. 3, где исследовались факторы населенности площадки и протяженности линий электропередачи. Обычно для критериев, у которых отсутствует существенная неопределенность, можно подобрать данные, характеризующие воздействие. В исследовании для WPPSS плотность населения на расстоянии до 80 км от предполагаемого объекта была табулирована. Расчеты по формуле (3.1) позволяют определить значения фактора плотности населения в окрестности данной площадки. Протяженность линий электропередачи была измерена по карте, где были обозначены возможные площадки и главные электрические сети.
При наличии неопределенности и для количественной оценки распределения вероятности воздействия только сбор данных обычно недостаточен — одновременно должны использоваться и другие подходы. Например, в исследовании для компании WPPSS были собраны данные, касающиеся окружающей среды в районе возможных площадок, количества лососевых, использующих ближайшие реки для нереста, размеры и финансовое состояние городов вблизи площадок и т. п. Эта информация использовалась при оценке биологического воздействия, воздействия на лососевых и социально-экономического воздействия. В § 6.2 первые два из них рассмотрены более подробно. По биологическому и социально-экономическому воздействиям вероятностей, оценки делались с помощью непосредственной экспертной оценки, имеющихся данных. Была построена небольшая модель для включений данных по лососевым в оценку воздействий. Различные иллюстрации социально-экономических воздействий, использующие более подробные модели, имеются и кратко обсуждаются в §6.5.
6.1.2. Моделирование процессов, вызывающих воздействия
Моделирование используется для количественного описания как детерминированных, так и вероятностных воздействий. При исследовании размещения ГАЭС, приведенном в гл. 9, экономическая модель используется для детерминированной оценки денежных затрат по каждой площадке, приведенных к первому году ее освоения. Вводимые в модель данные включают затраты на строительство объекта и линий электропередачи, приобретение необходимых земель, проектирование, управление строительством, обслуживание и лицензирование, эксплуатацию, а также накладные расходы и т. д. Результатом расчетов на модели является ряд затрат, приведенных к первому году. Подобная детерминированная экономическая модель использовалась в исследованиях для компании WPPSS.
Весьма значительное число неуправляемых факторов, влияющих на стоимость энергетических объектов, делает более предпочтительным построение вероятностной модели затрат. В качестве исходных данных для такой модели используется стоимость земель, геологические и сейсмологические данные, стоимость строительных материалов, данные по возможным задержкам в лицензировании различных компонентов объекта, производительности труда строительных рабочих, климатические условия (так как дожди или снегопады могут замедлить строительство), нормы процента на капитал и некоторые другие данные. Очевидно, каждый из этих факторов может оказывать значительное влияние на стоимость предполагаемого объекта и каждый из них может быть довольно неопределенным. Неопределенность может быть количественно оценена либо с помощью имеющихся в распоряжении или собранных данных, либо путем экспертных оценок.
Вероятностная модель может быть либо аналитической, либо имитационной. Ее назначение — описание взаимосвязи между набором входных и выходных экономических переменных. Входными переменными являются, например, строительные и эксплуатационные затраты на объекте по годам в течение его строительства и срока службы. Если входные данные имеют вероятностный характер, то и выходные данные модели также имеют вероятностный характер.

Рае. 6.1. Схема вероятностной модели воздействия
Графическая иллюстрация схемы вероятностной модели воздействия приведена на рис. 6.1. Эта схема обобщает третий этап анализа решений (т. е. описание возможного воздействия каждого объекта), показанного на рис. 2.1. Что должно быть включено во входные переменные, с какими они связаны критериями и каково распределение вероятности по всем входным переменным, должна определить экспертная оценка. По моделям воздействия существует обширная литература. Она содержит большой материал по имитационным и вероятностным методам, а также статистические данные. Эта литература указывается в данной главе по мере необходимости.
6.1.3. Прямая экспертная оценка
Как правило, прямая экспертная оценка необходима, когда существует неопределенность. При использовании распределения вероятности такая оценка была бы количественной. Имеются два основных способа выполнения этого: прямое определение всего распределения вероятности, а .также выбор стандартного распределения вероятности и прямое определение параметров для вида этого распределения. Из-за возможности больших разночтений при проведении анализа решений важным моментом является формализация экспертных оценок. Поскольку такая оценка необходима для решения ряда важных вопросов проблемы размещения, необходимо уделить этому достаточное внимание.
Прямая оценка дискретного распределения вероятности. Подход к оценке для переменных с дискретными и непрерывными уровнями разный.
Предположим, критерий (или входная переменная) Y имеет возможные дискретные уровни yk, где k = 1, ..., К. В некоторых случаях уровни у могут быть ранжированы. Однако каждый г/д должен существовать и встречаться только один раз. Это означает, что они взаимоисключающи и совокупно исчерпывающи. Задача заключается в определении вероятности Рk, k = 1,.... К., имеющихся уровней yk. Теоретически задача проста. К эксперту, чье мнение нас интересует, обращаются с просьбой количественно оценить Pk. Однако на практике эксперт может потребовать помощи в виде разъяснения условий поставленной задачи. Для типичного случая, когда необходима помощь, процесс оценки может быть следующим.
Во-первых, вероятности для различных индивидуальных уровней у должны быть упорядочены и расположены от больших вероятностей к меньшим. Предположим, что порядок такой последовательности У1, У2, ...., Уk. В таком случае
![]() (6.1)
(6.1)
Если же вероятности ук и ук+1 равны, то
![]() (6.2)
(6.2)
Следующий шаг может заключаться в некоторых сравнениях. Например, эксперт может считать, что ух более вероятен, чем у2 или у3, т. е.
![]() (6.3)
(6.3)
Кроме того, сумма этих вероятностей должна быть равна 1, так как у к взаимоисключающие и коллективно исчерпывающие. Поэтому
![]() (6.4)
(6.4)
Набор таких уравнений, как (6.1) — (6.3), вместе с (6.4) должен значительно ограничить диапазон возможных вероятностей. И этого было бы достаточно для качественных сравнений и нахождения более вероятного результата.
Обычно, однако, требуются количественные оценки того, насколько один результат более вероятен, чем другой. К примеру, эксперт может считать, что у2 в 2 раза вероятнее, чем у с
![]() (6.5)
(6.5)
Для проверки и оценки Рк чаще используется внешняя характеристика. Такой подход иллюстрируется на рис. 6.2. Эксперту предлагают на выбор две лотереи. Одна из них имеет непосредственное отношение к проблеме, другая совершенно не имеет к ней отношения.
Если эксперт выбирает лотерею I, он получает выигрыш при исходе ук, в противном случае не получает ничего. Если выбрана лотерея II, вероятность выигрыша q, отсутствия выигрыша 1 — q.
Вероятность q может быть установлена с помощью урны с красными и белыми шарами. Например, если 40 из 100 шаров красные, вероятность q равна вероятности вытаскивания красного шара 0,4. Изменением числа красных и белых шаров вероятность q варьируется до тех пор, пока результаты эксперта не станут равноценны в этих двух лотереях. Определим вероятность, соответствующую этому моменту, как qk. Вследствие равноценности лотерей вероятность yк соответствует qk, когда вероятности выигрыша в обоих лотереях равны
![]() (6.6)
(6.6)
Набор уровней q, который следует ожидать для Рк, значительно уменьшается, если начинать издалека. Если положим, что Рк может быть примерно равным 0,2, можно принять значение q = 0,9 (рис. 6.2) и попросить эксперта сделать выбор. Конечно, в этой ситуации будет выбрана лотерея II. Это поможет обеспечить лучший контакт с экспертом и позволит ему начать решать задачу с более легкого вопроса. Все это позволяет эксперту вдуматься в трудности поставленной задачи.
Следующий уровень q для сравнения может быть принят 0,6. Снова лотерея II оказывается предпочтительнее. Это уже прямой намек на то, что Pк <0,6. Затем можно сделать скачок к q = 0,05, и если Рк действительно близко к 0,2, то предпочтительнее лотерея I и, значит, Рк> 0,05. Вероятность q возрастает, когда предпочтительнее лотерея I, и падает, когда предпочтительнее лотерея II. При использовании метода схождения эксперт должен в конечном счете стать безразличным к выбору лотереи. Если это произойдет при q = 0,25, то следует положить Рк = 0,25.
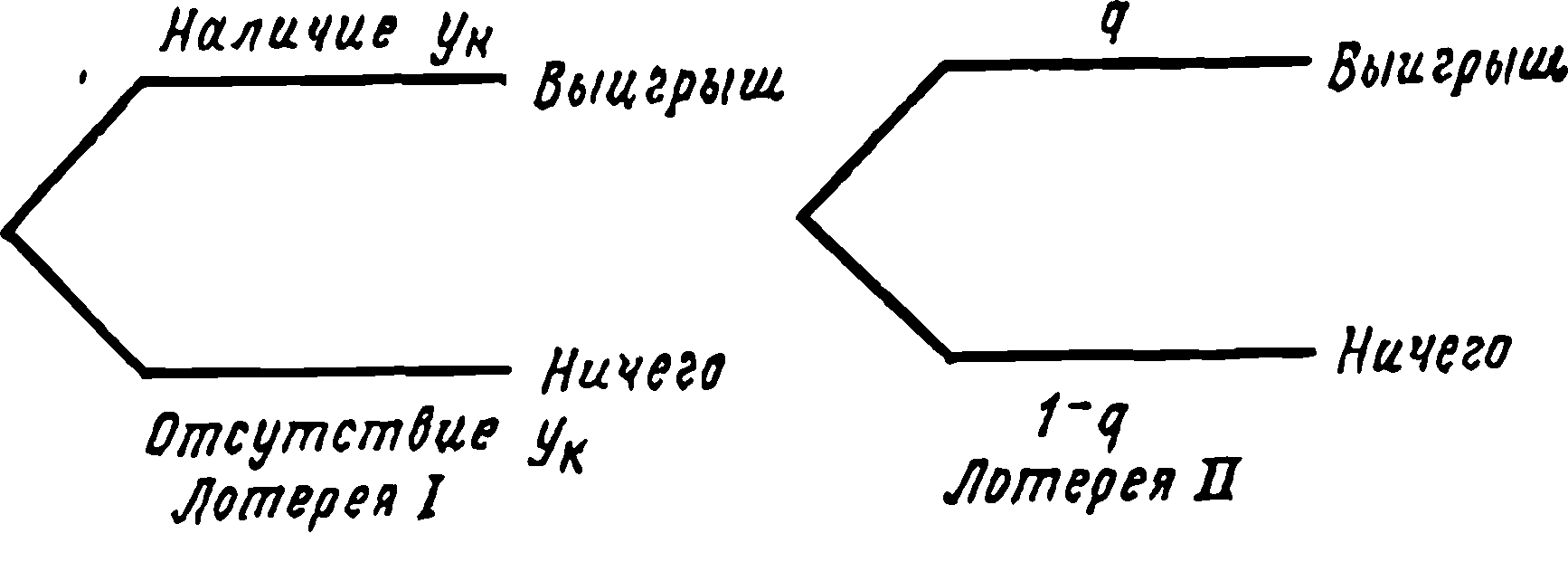
Рис. 6.2. Оценка вероятности исхода ун в лотерее
С использованием таких уравнений, как (6.1) — (6.6), могут быть получены достаточно точные или точные оценки для Р1,..., Рк. Затем должна быть проведена последовательная проверка. Она заключается в постановке большего числа вопросов (аналогичных вышеуказанным) и преследует цель выяснения того, насколько оценки Ph соответствуют поставленным вопросам. Если эксперт сказал, что ух по крайней мере в 3 раза вероятнее, чем у2, то Р1>3 Р2. Если у1 или у2 более вероятно, чем все другие возможные уровни, то Р1+ Р2 >0,5; а если у6 на 10% более вероятно, чем ут, то очевидно, что Р6 = 1,1 Р7. Если обнаруживается непоследовательность оценок, необходимо принять меры для устранения этого.
Не исключено, что непоследовательность будет обнаружена. Фактически главная цель формализации мнений заключается в идентификации и устранении непоследовательности. Проблема связана с индивидуальными качествами эксперта и его способностью держать в голове последовательность использования всей необходимой информации. Как правило, большинство людей предпочитают умножать восемь чисел на бумаге, а не в уме, из-за боязни ошибки. Поэтому более разумно, например, написать восемь вероятностей (т. е. к = 8) на бумаге для того, чтобы оценить их, сопоставить и исключить какую-либо непоследовательность в оценках.
Прямая оценка непрерывного распределения вероятности. Для непрерывного распределения рассмотрим критерий (или входную переменную) Y с уровнями у. Определим вероятность того, что уровень Y меньше или равен у для каждого возможного у.
Рассмотрим конкретный пример, используя недавнее исследование по размещению нефтеприемного порта в Кодиак Айленд, штат Аляска 1. Этот энергетический объект необходим в связи с добычей нефти в прибрежных районах западной Аляски. С точки зрения воздействия на окружающую среду предметом заботы были морские птицы, обитающие вблизи предполагаемого объекта. Критерием было количество морских птиц, гнездящихся по соседству с объектом. Необходимо было получить распределение вероятности для этого критерия, т. е. получить кривую, подобную той, которая показана на рис. 6.3. Вопрос заключается в том, как получить эту кривую.
Для наглядности положим, что местный орнитолог живет близко от района, где гнездятся птицы. Исследователи хотели бы оценить его мнение относительно имеющегося числа морских птиц.

Рис. 6.3. Распределение вероятности, что число морских птиц а окрестности объекта равно у или меньше (экспертные оценки):
А — точка, характеризующая оценку эксперта
Сначала можно попросить эксперта оценить число птиц таким образом, чтобы он был уверен, что действительное число наверняка превышает его оценку. Очевидно, что ответ «нуль птиц» является одним из правильных ответов. Но можно пожелать увеличить оценку, насколько это возможно. Положим, что эксперт ответил, что число птиц 25 тыс. Это число устанавливает нам первый нижний предел. Далее эксперта просят дать верхнюю оценку, которая заведомо выше действительного числа. Эта оценка может быть 120 тыс. Каждая из таких оценок является предметом изучения в выполняемой нами процедуре.
На следующем этапе эксперта просят дать среднюю оценку, обозначенную у, такую, чтобы он считал: вероятность того, что у< у, равна 0,5. Можно прямо попросить сделать такую оценку или использовать в качестве аналога схему рис. 6.2. Это показано на рис. 6.4. При выборе лотереи III орнитолог получает желаемый выигрыш, если подлинное число птиц у меньше или равно произвольно выбранному числу у', в противном случае он не получает ничего. В лотерее IV орнитолог имеет вероятность 0,5 либо получить выигрыш, либо не выиграть. Такое значение вероятности обеспечивается при бросании монеты.
Идея заключается в том, чтобы начать с легких вопросов о выборе, используя оценку у', а затем перейти к более трудным. Две лотереи равноценны, когда вероятность того, что у < у', равна 0,5, а это значит, что у = у'. Сначала значение у' может быть установлено в 30 тыс.
Орнитолог, вероятно, выберет лотерею IV, так как 30 тыс. только не намного больше его минимальной оценки 25 тыс. Если выбрана лотерей IV, оценка у' увеличивается, скажем, до 50 тыс. Опять лотерея IV оказывается предпочтительнее. Теперь у' принимается равным 90 тыс. и орнитолог предпочитает лотерею III. Затем оценка снижается, допустим, до 70 тыс. Здесь лотерея IV может оказаться предпочтительнее, но при 75 тыс. снова предпочтительнее лотерея III. Это означает
![]() (6.7)
(6.7)
Таким образом, у = 75 тыс. Точка, соответствующая у = 75 и р = 0,5, наносится на график, как это показано на рис. 6.3.
В приведенной последовательности оценок значение у соответствует вероятности 0,5. Рассмотрим теперь другие значения вероятностей: 0,01; 0,25; 0,75 и 0,99 и получим соответствующие точки. 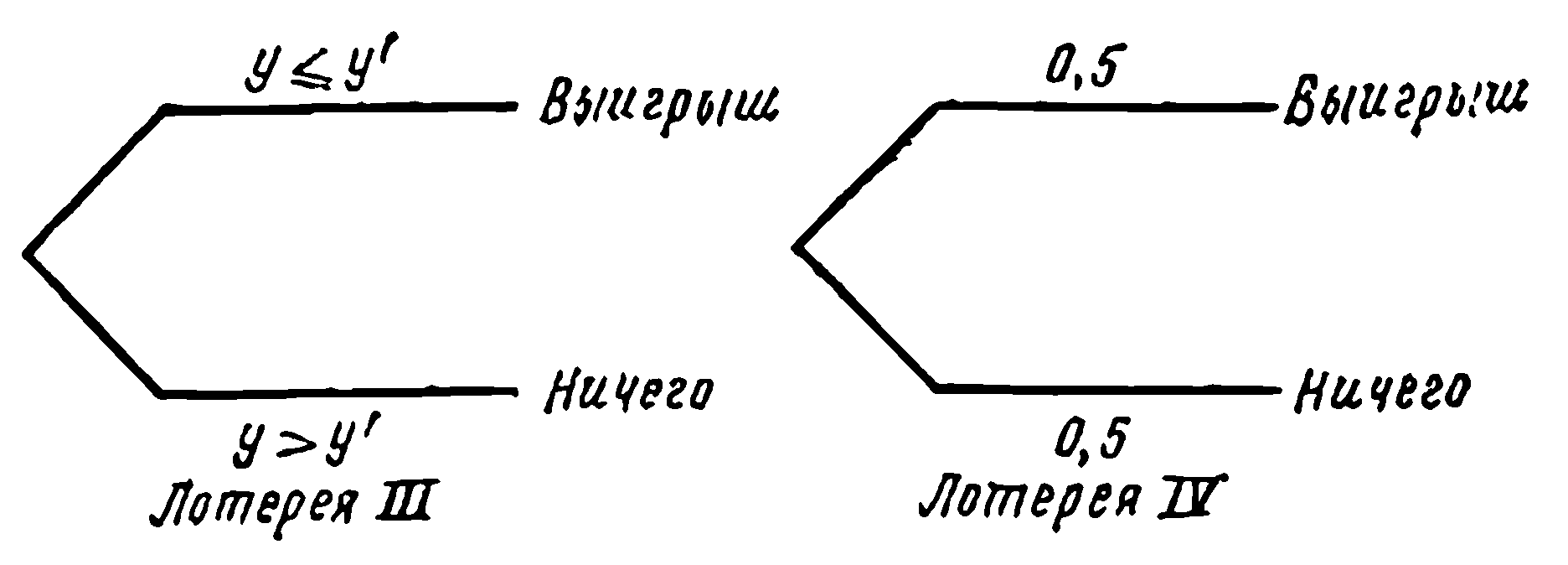
Рис. 6.4. Оценка среднего значения непрерывного распределения вероятности
Это может быть сделано аналогичным путем, но с заменой 0,5 в лотерее IV рис. 6:4 на 0,01 для значения вероятности 0,01 и т. д. Предположим, что вероятностям со значениями 0,01; 0,25; 0,75 и 0,99 соответствуют оценки 40, 60, 85 и 100 тыс. птиц. Тогда
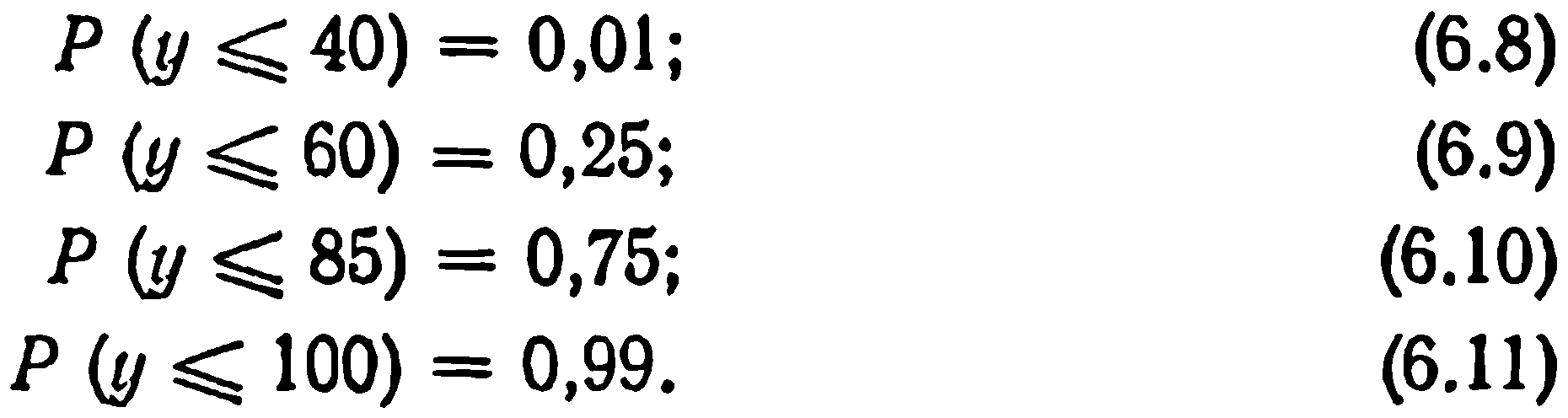
Соответствующие точки также нанесены на график рис. 6.3. Кривая, которую они образуют, является распределением вероятностей числа морских птиц, гнездящихся в рассматриваемом районе, с точки зрения орнитолога. Используя кривую, можно указать вероятность того, что число морских птиц меньше любого установленного их количества.
Как и при дискретном распределении-вероятностей, необходимо позаботиться об обеспечении последовательности суждений. Например, из рис. 6.3 следует, что вероятность определения точного числа морских птиц меньше 60 тыс. равна вероятности того, что точное число находится между 60 и 75 тыс. Другой пример: число птиц большее 75 тыс. равновероятно их числу, большему или меньшему 85 тыс. Кроме того, по кривой можно установить, что вероятность того, что в районе обитает меньше 50 тыс. птиц, должна быть около 10% (т. е. 0,1). Когда обнаруживается непоследовательность эксперта в его оценках, как и в случае дискретного распределения вероятностен, должны быть сделаны изменения в некоторых оценках. Если это необходимо, привлекаются дополнительные варианты. Процесс можно считать оконченным, когда эксперт станет последовательным в его оценках.
Оценка параметров распределения вероятностей. Часто есть основания полагать, что представляющий интерес критерии (или переменная) может быть адекватно описан стандартным распределением вероятностей, таким как нормальное распределение или распределение Бернулли. В этом случае для получения полного распределения необходимо только определить его параметры.
Покажем это на примере. Положим, было решено, что для рассмотренных оценок популяции морских птиц подходит нормальное распределение. Распределение вероятности в этом случае будет иметь вид
 (6.12)
(6.12)
где у и σ — среднее и стандартное отклонения у. Они могут быть оценены различными путями. Например, вероятности 0,5 и 0,25 из (6.7) и (6.9), подставленные в (6.12), дают два уравнения с неизвестными у и σ. Они могут быть решены относительно у и σ с использованием обычных таблиц для у и σ.
В качестве альтернативы возможна оценка у и σ с помощью непосредственного опроса. Поскольку нормальное распределение вероятности симметрично, наиболее вероятный уровень Y равен среднему значению. Следовательно, наиболее вероятным уровнем Y будет у в (6.12). Стандартное отклонение не имеет такой простой интерпретации. Вероятность того, что действительное число птиц попадает в пределы одного стандартного отклонения от среднего значения, составляет приблизительно 0,64. Возможен прямой вопрос для такой оценки, но для профессионала, вероятно, легче ответить на вопрос о значении вероятности, с помощью которой стандартное отклонение может быть легко вычислено. Оценки воздействия на лососевых в случае исследования для компании WPPSS, описанного в п. 3.3.2, производились путем определения среднего и стандартного отклонений для нормального распределения вероятностей. Более подробно это обсуждается в п. 6.2.3.
В некоторых случаях сама вероятность является искомым параметром распределения. Это, например, имеет место в случае распределения Бернулли. Здесь рассматривается ситуация, когда какое-то событие либо происходит, либо не происходит и необходимо знать вероятность того, что оно произойдет. В качестве иллюстрации можно привести анализ риска при сооружении порта по приемке импортного сжиженного природного газа, обсуждаемый в § 6.8. Он включает вероятность столкновений судов, приводящих к разливу сжиженного газа. Газ может либо немедленно воспламениться, либо нет. Вероятность этого может быть установлена с помощью схемы, приведенной на рис. 6.2, в которой у определяется как «воспламенение разлившегося сжиженного газа».
Обобщение распределения вероятностей. В некоторых случаях, когда краппе затруднены или невозможны сбор данных и (или) разработка модели какого-либо процесса, получение функции распределения вероятностен также представляет трудную задачу. В этих случаях возможно достаточно простое обобщение информации с помощью «лучшей оценки». Затем с использованием анализа чувствительности можно проверить, насколько она точна.
Например, «лучшей оценкой», касающейся морских птиц, может быть определение количества таких птиц, живущих поблизости, допустим в пределах 8 км от предполагаемого энергетического объекта. Другой пример, используемый в оценке возможных значений критериев в исследовании для компании WPPSS, касается количества домашних хозяйств вблизи возможной площадки, для которых дополнительно появится определенное количество туманных дней в году вследствие существования энергетического объекта. Метеоролог с профессиональным знанием местной погоды, рельефа местности и сведениями о предлагаемой системе охлаждения конденсаторов турбин электростанции чертит контуры районов, в которых ожидается 1,2 ... дополнительных туманных дней в году. Рассматривая эти районы на карте, просто подсчитывается количество учитываемых домов для установления «лучшей оценки». Формально метеорологическая модель в таком случае не разрабатывается; обобщение информации производится непосредственно самим метеорологом.
Может существовать воздействие, не имеющее неопределенности в уровнях. Такое воздействие в сущности является частным случаем воздействий, содержащих неопределенность (т. е. она равна нулю). Тогда многое из того, что было сказано о последовательности и технике оценки общего случая, имеет также отношение и к этому частному случаю.
Вопросы методологии определения воздействий
Рассмотрим два вопроса, играющих важную роль в анализе воздействий: вероятностные зависимости между критериями и предубежденные или ошибочные мнения.
Вероятностные зависимости между критериями. О сложности вероятностных зависимостей между критериями можно судить по п. 2.3.3. Суть дела заключается в том, что для данной площадки знание уровня одного критерия будет влиять на оценку уровней других критериев. Важно знать, присуща ли эта зависимость данной конкретной площадке. Может быть, что два (или более) критерия являются зависимыми для одной площадки и независимыми для другой. Рассмотрим два примера воздействий, в которых можно ожидать такой зависимости, и два различных способа решения этого вопроса. Для первого примера используем исследования для компании WPPSS (гл. 3). Напомним, что воздействие на лососевых для каждой площадки описывалось двумя критериями: количеством рыбы в реке и процентом ежегодных потерь вследствие миграции, отлова, гибели и т. д. Количество лососевых в реке было определено по многолетним статистическим данным, тогда как процент потерь был оценен с помощью вероятностных методов с использованием экспертных оценок. Предположим, что необходимо оценить то и другое с помощью вероятностных методов.
Назовем количество рыбы в реке критерием Y, а процент потерь, критерием Z. Их уровни будут соответственно у и z. Положим, что в то время как оценки количества рыбы увеличиваются, оценки процент потерь уменьшаются. (Отметим, что это может быть, так же как может иметь место и увеличение абсолютных потерь рыбы при увеличении количества рыбы в реке.) Подобная зависимость может, например, объясняться большим количеством рыбы, связанным с большим количеством воды в реке, что в свою очередь обусловливает меньшую долю ее, используемую на охлаждение конденсаторов турбин электростанции. Следовательно, тепловое воздействие на единицу объема воды уменьшается и для каждой рыбы снижается вероятность того, что она будет подвергаться отрицательному воздействию. Это снижает процент потерь рыбы. Для использования такой зависимости необходимо, во. первых, оценить функцию плотности вероятности fу (у) для количества рыбы в реке. Затем для каждого значения у в реке необходимо оценить условную функцию плотности вероятности fy/z (z/y) для потерь. Объединенная плотность вероятности, используемая в анализе,
![]() (6.13)
(6.13)
Из (6.13) можно вычислить вероятности для у и г в рассматриваемом диапазоне.
Второй пример касается последствий воздействий от различных факторов, вызываемых общими причинами. Рассмотрим проблему размещения мощной электростанции на угле. Предположим, что проблема оценивается по двум критериям Q и R, характеризующим соответственно количество дней болезни жителей с респираторными заболеваниями и количество жителей, страдающих от загрязнения воздуха. Непосредственно оценка плотности суммарной вероятности h для этих двух критериев затруднительна из-за вероятностного характера проявления этих последствий. Вместо этого можно определить однокритериальную плотность вероятности для hQ и из распределения вероятностей, метод получения которого рассмотрен в п. 6.1.3.
Уровни Q и R зависят от загрязнения воздуха двуокисью серы, которое обозначим через S c уровнями s. Решение заключается в оценке плотности вероятности hs уровней загрязнения и затем в оценках плотностей вероятности для Q и R в зависимости от S. При этом предполагается, что Q и R вероятностно условно взаимонезависимы для данного S. Это менее сильное допущение, чем допущение о полной независимости. При таком допущении
![]() (6.14)
(6.14)
Данные, собранные в исследовании для WPPSS по нескольким возможным площадкам (табл. 3.5), подтверждают такую зависимость: большее количество рыбы в реке — меньший процент ее потерь.
Этим выражением 2 взвешиваются различные вероятности q и r парами по критерию S с учетом вероятности s. Подробно эти вероятностные зависимости представлены в стандартных таблицах, например в 121, 221.
Эти примеры касаются главным образом ситуации, когда для получения распределений вероятностей используются экспертные оценки. Если имеются достаточно представительные данные и модель процесса воздействий разработана, нет необходимости в разработке специальной методологии количественного определения вероятностных зависимоcтей. Систематизация и табулирование данных должны включать и вероятности их значений. Систематизация данных должна также предусматривать и повторяемость во времени различных комбинаций уровней критериев (или переменных) в большей степени, чем повторяемость уровней отдельных критериев. Модель воздействия должна описывать механизм, который приводит к результирующим зависимостям. Если все это сделано надлежащим образом, то результатами моделирования будут вероятностные зависимости.
Предубежденные мнения. Предубеждение в экспертных оценках встречается часто. Превосходное обсуждение многих вопросов такого предубеждения дается в 123]. Здесь мы рассмотрим некоторые важные аспекты этой стороны дела. Предубеждения полезно разделить на те, в которых эксперты, высказавшие мнение, признаются, и на те, в которых не признаются.
Иногда эксперт намеренно высказывает предубежденное мнение, неизменно не соглашаясь с оценками других экспертов. Например, эксперт может предпочитать площадку площадке S2, и как следствие этого предубеждение может выражаться в том, что оценка стоимости для площадки S1 занижается, а для площадки S2 завышается. Другой причиной предубеждения является игнорирование анализа или, возможно, приверженность групповому ложному мнению. Если при опросе даются «странные» ответы, то их анализ может вызвать недоверие к эксперту. В любом случае возможность предубеждения должна иметься в виду вне зависимости от используемой методологии. При этом, очевидно, должны быть предусмотрены условия для того, чтобы другие эксперты или заказчики могли выявить предубежденную информацию.
1 Краткое описание этого исследования приводится в п. 7.7.3.
2 Главное достоинство выражения (6.14) заключается в возможности учета в логического объединения информации из разных источников. Так, инженер может лучше информировать о выбросе двуокиси серы и характеризовать hs. Медик — относительно заболеваемости и Hqjs, а социолог может оценить, основываясь на общественном мнении.
Другим источником намеренной предубежденности может быть система вознаграждений, которая содействует нечестности. Если представители проектно-строительной фирмы заявляют, что фирма может построить объект за 100 млн. долл., а не за 125 млн. долл., которые действительно потребуются, они имеют больше шансов заключить контракт на строительство объекта. С другой стороны, вознаграждение за строительство объекта стоимостью в 100 млн. долл, значительно ниже, чем за объект стоимостью 125 млн. долл.
Из-за такой системы вознаграждении «де-факто» сначала возникают низкие оценки стоимости, так как в результате профессионального предубеждения первоначальные оценки занижаются. В исследованиях по размещению энергетических объектов для уменьшения предубежденности экспертов необходимо просвещение руководства относительно вероятностного характера задачи. Эксперты и исследователи могут существенно способствовать объективности оценок путем формулирования ясных предположений, исходя из которых делаются экспертные оценки, а также проведения оценки предположений, касающихся возможных площадок
Типичным предубеждением, которое часто не признается экспертами, является наблюдающаяся приверженность экспертов к первоначальным оценкам. Такие случаи относятся к ситуациям, в которых делается серия оценок. Случается, что более поздние оценки в серии оценок находятся ближе к первоначальным оценкам, чем они должны были бы быть при отсутствии предубеждения.
Для примера обратимся к рис. 6.3, где обсуждались оценки числа морских птиц в окрестностях предполагаемого нефтеприемного порта, Первая точка определялась для вероятности 0,5, что соответствовало 75 тыс. птиц, и она определялась выражением (6.7). Следующая точка определялась для вероятности 0,25. Обычно процесс оценки начинается со значения 75 тыс. птиц, а затем числа уменьшаются до тех пор, пока не достигается значение вероятности 0,25. Большое количество данных показывает, что отдельные эксперты не продвигаются далеко от начальной точки, привязываясь к ней, «как к якорю» (в данном случае к вероятности 0,5, соответствующей 75 тыс. птиц).
Другой пример — оценка затрат на приобретение воды для различных площадок. Поскольку одна и та же процедура экспертных оценок используется для всех площадок, все предубежденные оценки экспертов могут тяготеть к первоначальной оценке.
Имеется и другой механизм формирования предубежденности в экспертных оценках. В анализах размещения порта по приемке импортной нефти может оказаться необходимой оценка количества разлившейся нефти в результате катастрофы. Если случай большого разлива нефти произошел недавно и имел широкую огласку, то оценки, вероятно, будут завышенными по сравнению с тем случаем, когда гласность отсутствует. Проводившиеся оценки подтвердили это. Существуют и другие разновидности предубеждений в мнениях экспертов. Понимание процедур, используемых экспертами при формировании их мнений, может облегчить задачу выявления предубеждения. Предлагая эксперту рассмотреть проблему с другой точки зрения, можно избавить его от предубеждения. Пример такого подхода, направленного на схождение оценок путем приближения к результату с двух сторон, приведен в п. 6.1.3.
6.1.5. Результаты количественной оценки воздействий
Практически во всех задачах по определению возможных воздействий энергетических объектов для каждой рассматриваемой площадки используются комбинации данных о воздействиях, их моделей и мнений экспертов. Эти комбинации могут использоваться как отдельно для некоторых критериев, так и для их совокупности.
В каждой проблеме размещения и, конечно, в каждом анализе решении экспертные оценки должны прямо или косвенно использоваться. Если для оценки воздействия имеются количественные данные, мнения экспертов должны использоваться для определения необходимого объема таких данных и их отбора. Если строится модель воздействий, мнения экспертов используются для разработки модели и обеспечения входной информации. И, конечно, если при решении проблемы используется прямая оценка информации, то без мнения экспертов обойтись невозможно. Необходимо выработать позицию относительно баланса рассмотренных подходов при оценке воздействий. Правильный баланс основывается на учете времени и стоимости анализа в каждом отдельном случае. Важное значение для окончательного выбора площадки имеет правильная оценка роли различных воздействий. Поскольку такая оценка делается до того, как становятся известны результаты анализа, группе экспертов по оценке размещения объекта после получения предварительных результатов может быть предложена переоценка роли воздействий. Вследствие этого некоторые этапы исследований иногда повторяются для учета более полных и точных данных, чтобы использовать лучшую модель или сделать более тщательную прямую оценку.
Таким образом, для корректного решения задачи большое значение имеют тщательность и правильная направленность исследований. Например, может быть легко установлено, что три из девяти площадок значительно хуже других шести, даже если принимать во внимание только худшие значения показателей последних. В этом случае, очевидно, нецелесообразно тратить усилия на изучение этих трех площадок. Если мнения экспертов при оценке площадок расходятся, существенным является вопрос — оправданы или нет попытки согласования этих мнений (см. гл. 7).
В каждом методе оценки площадки для энергетического объекта используются какие-либо данные, модели и мнения экспертов. Когда все это используется должным образом, все методы, включая анализ решений, позволяют ясно судить о том, где и как получить данные и как должна строиться модель.
Задача может быть решена более успешно, если:
определены и устранены умышленные или неумышленные предубеждения;
выявлению лучшей площадки будет хорошо помогать модель размещения;
корректность процесса выбора площадки и справедливость самого выбора будут поддержаны административными органами.
В § 6.2—6.6 обращено особое внимание на пять главных групп факторов проблемы размещения: окружающей среды, экономики, социально-экономических, здоровья и безопасности людей, общественного мнения.
Основные подходы к оценке воздействий, рассмотренные в§6.1, могут быть использованы при анализе всех этих групп факторов. Группы моделей, разработанных для каждой группы факторов, рассматриваются в § 6.2—6.6, где показаны их главные отличия и общие черты. В § 6.7 и 6.8 более подробно рассмотрены два важных случая применения моделей.

