Контакт расплавленного топлива с теплоносителем, возможный в процессе аварии реактора с жидкометаллическим теплоносителем, рассматривается как один из опасных эффектов, поскольку он может привести к быстрому нагреву натрия и взрыву натриевых паров. Как уже говорилось, в течение неконтролируемого аварийного процесса возникают ситуации, когда взаимодействие жидкого топлива с теплоносителем может повлиять на ход аварии. Особый интерес представляет роль натриевого теплоносителя в разрушении активной зоны.
При взаимодействии расплавленного топлива с теплоносителем дае среды перемешиваются между собой настолько, что теплоотдача к натрию становится во много раз больше, чем при кипении натрия в каналах ТВС. При этом давление паров натрия быстро растет, и происходит расширение натрия, находящегося в двухфазном состоянии. Поскольку температура кипения натрия значительно ниже температуры плавления топлива, в процессе взаимодействия натрий становится более эффективной рабочей жидкостью, чем расплавленное топливо. Следовательно, если считать, что разрушение активной зоны происходит под действием расширяющегося натрия, повреждения внутриреакторных конструкций будут более серьезными, чем в случае расширения жидкого топлива.
Считается, что взаимодействие расплавленного топлива с теплоносителем может быть двух видов: сильное взаимодействие (взрыв паров) и слабое взаимодействие (интенсивное кипение). При взрыве паров передача тепла от топлива к натрию осуществляется значительно быстрее, чем при расширении смеси топлива с натрием. При этом значительная доля тепловой энергии, содержащейся в топливе, преобразуется в механическую и передается внутренним конструкциям реактора. В случае слабого взаимодействия теплообмен между топливом и натрием менее интенсивен, и механическое воздействие на конструкции, оказываемое расширяющимся натрием, мало. Хотя масса натрия над активной зоной сдерживает расширение паров в области взаимодействия топлива с натрием, тем не менее даже при слабом взаимодействии механическая энергия, выделяемая при испарении натрия, будет больше, чем только при расширении топлива.
Исследования, касающиеся разрушительных последствий взаимодействия расплавленного топлива с натрием, проводятся в двух направлениях. Во-первых, исследуется влияние различных явлений, характеризующих процесс взаимодействия, на количество выделяемой механической энергии. Во-вторых, большое внимание уделяется физике процесса взрыва паров. Ниже приводится описание некоторых моделей процесса расширения натрия, затем рассматриваются вопросы, связанные с процессом взрыва паров.
А. МОДЕЛИ ПРОЦЕССА РАСШИРЕНИЯ НАТРИЯ
Модель Хикса—Мензиса
Впервые количественные исследования процесса взаимодействия расплавленного топлива и теплоносителя в реакторах БН были проведены Хиксом и Мензисом [3], которые на основе законов термодинамики рассчитали максимально возможное значение механической энергии, выделяемой натрием при определенном значении тепловыделений активной зоны. На рис. 16.4 приведены результаты расчетов, выполненных для начальных значений температуры топлива 3450 К и температуры натрия 1150 К. На рисунке представлена зависимость механической работы расширения натрия от отношения масс натрия и топлива, а также конечного значения давления в активной зоне1.
Как предполагалось, максимально возможное значение высвобождаемой механической энергии увеличивается с уменьшением конечного давления. Нелинейный характер зависимости энергии от отношения масс натрия и топлива можно объяснить следующим образом. Если доля натрия в смеси с топливом мала, количество совершенной механической работы PdV незначительно. Если же доля натрия очень велика, то большая теплоемкость препятствует повышению температуры натрия. Максимальное значение выделяемой механической энергии соответствует отношению масс натрия и топлива, равному приблизительно 0,1 (такое соотношение масс натрия и топлива характерно для реакторов БН).
При проведении расчетов предполагалось, что процессы проходят в условиях термического равновесия. Принималось также, что свойства материалов не зависят от температуры, отсутствует выделение тепла за счет ядерной реакции деления в топливе. Пары натрия рассматривались как идеальный газ. Наиболее важную роль играет первое допущение, которое означает, что в процессе расширения натрия обеспечивается эффективный теплообмен между топливом и натрием. Таким образом, расчеты можно считать чисто термодинамическими.
В соответствии с моделью, предложенной Хиксом и Мензисом, процесс взаимодействия расплавленного топлива с натрием можно разделить на два этапа. На первом этапе происходит смешивание топлива с натрием, сопровождаемое обменом тепла между ними, который заканчивается, когда температуры обоих компонентов смеси выравниваются, т. е. наступает тепловое равновесие. На втором этапе натрий испаряется и, увеличивая свой объем, совершает работу PdV, за счет которой происходит деформация или перемещение внутриреакторных элементов, прилегающих к активной зоне. В процессе расширения, когда температура натрия падает, тепло продолжает поступать к натрию от топлива, за счет чего поддерживается тепловое равновесие двух жидкостей. (Физический смысл этого состоит в предположении, что перенос тепла осуществляется с бесконечно большой скоростью на участке, характеризуемом бесконечно малым перепадом температур. Именно поэтому расчеты дают предельную оценку количества выделяемой энергии.)
На рис. 16.5 приведена схема процесса нагревания и расширения натрия в диаграмме Т — s. Точка 1 диаграммы соответствует начальному состоянию жидкого натрия при температуре насыщения. За счет тепла расплавленного топлива происходит разогрев натрия до состояния, обозначенного точкой 2, или до сверхкритической температуры (точка 3)1. Процесс расширения, сопровождаемый переносом тепла от топлива к натрию (в соответствии с моделью Хикса—Мензиса), показан линиями 2—2Б и 3—ЗБ.
1 Критическое значение температуры для натрия составляет 2509 К. Уравнение насыщенных паров натрия приведено в §11.4.
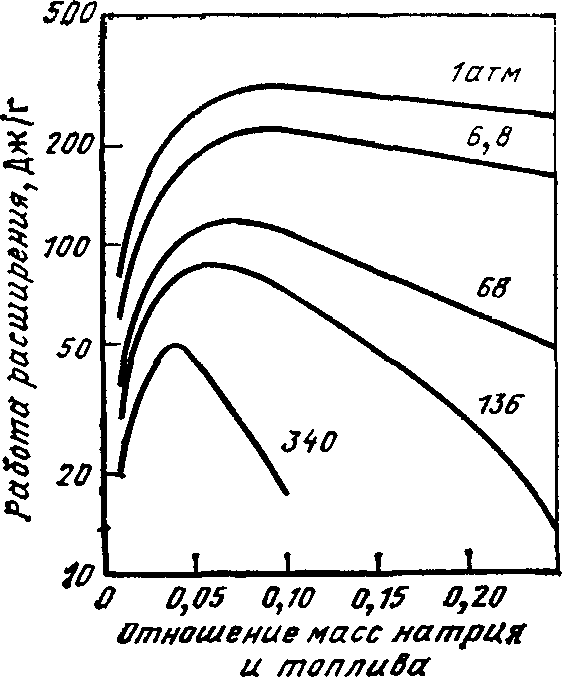
Рис 16.4 Работа, совершаемая при расширении топлива (данные Хикса—Мензиса при начальных значениях температуры топлива 3450 К и температуры натрия 1150 К и различном конечном давлении) [3]
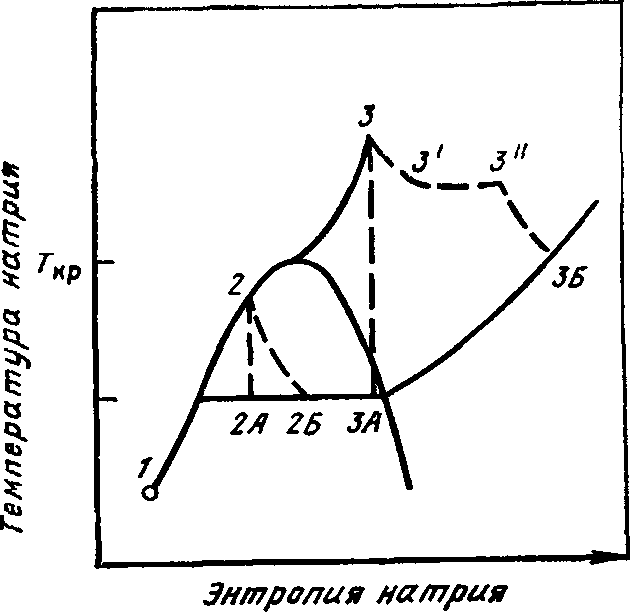
Рис. 16.5. Гипотетический аварийный процесс разрушения активной зоны, построенный в Г — s-диаграмме для натрия (Ткр — критическая температура; 3А—3Б — линия постоянного давления)
Однако можно предположить, что расширение нагретого натрия происходит так быстро, что энтропия натрия остается постоянной (линии 2—2А, 3—ЗА). В этом случае количество высвобожденной механической энергии будет значительно меньше по сравнению с предельной оценкой по методу Хикса—Мензиса. На участке 3—3' тепло к натрию передается от расплавленного топлива, на участке З'—З" расширение натрия происходит при постоянной температуре, в то время как топливо затвердевает; участок 3"—ЗБ соответствует теплообмену натрия с твердым топливом.
Если предположить, что в процессе смешивания топлива с натрием фазовых изменений не происходит и удельные теплоемкости веществ постоянны, то температура натрия в смеси перед началом расширения определяется следующим выражением:
![]() (16.7)
(16.7)
где индексы f и Na означают, что параметры относятся к начальному состоянию топлива и натрия соответственно. Величина т есть отношение массы натрия к массе топлива. Механическая энергия, передаваемая внешним элементам конструкции, выделяется при расширении натрия. Топливо передает тепло натрию, и температура двух составляющих смеси поддерживается одинаковой. Процесс расширения можно считать адиабатическим. Уравнение первого закона термодинамики для процесса расширения заданной массы смеси натрия и топлива можно записать в следующем виде:
![]() (16.8)
(16.8)
где dW — PdV— работа расширения натрия: dll = dUNa + dUf.
Это уравнение было использовано Хиксом и Мензисом. Значение W определяется равновесной температурой Тeq смеси перед началом расширения.
Маловероятной представляется возможность достижения критической температуры натрия Ткр. Если происходит взрыв паров, температура натрия.
не превысит значение, при котором происходит спонтанное образование пузырьков кипения (0,9Ткр, см. § 16.3). Если взаимодействие расплавленного топлива с натрием происходит менее интенсивно (слабое взаимодействие), теплоперенос от топлива к натрию ухудшается, что ограничивает нагрев натрия. В этом случае нельзя принимать бесконечно большое значение скорости теплопереноса, как в модели Хикса—Мензиса, в связи с чем расчетное значение механической энергии расширения натрия уменьшается. Основными причинами уменьшения теплопередачи от топлива к натрию являются низкая теплопроводность топлива, а также термическое сопротивление паров натрия и газообразных продуктов деления.
Модели, учитывающие нестационарный характер процесса взаимодействия топлива с натрием
Процессы теплопередачи и массопереноса при взаимодействии топлива с натрием — нестационарные. Учет зависимости от времени интенсивности этих процессов приводит к снижению расчетного значения выделяемой механической энергии по сравнению с ее значением, полученным по методике Хикса—Мензиса. Ниже рассматриваются основные особенности расчетных моделей нестационарных процессов.
Прежде всего необходимо учитывать влияние термического сопротивления топлива на скорость теплопередачи. За счет температурного градиента внутри топлива обеспечивается перепад температур между топливом и натрием. Дополнительное термическое сопротивление представляет зона контакта топлива и натрия, в особенности — при наличии паров натрия и газообразных продуктов деления. Кроме того, время, необходимое для дисперсии топлива и смешивания его с натрием также увеличивает общую продолжительность процесса расширения.
Перемещение расширяющегося натрия в зоне его взаимодействия с топливом сдерживается неподвижными прилегающими элементами, а также массой более холодного натрия над активной зоной. Различают две фазы действия сдерживающих факторов в процессе расширения натрия.
В начале процесса сопротивление движению натрия создается за счет передачи давления от зоны взаимодействия через массу натрия, расположенного над активной зоной, в виде звуковой волны. Для этого этапа зависимость давления Р от скорости V верхней границы зоны расширения можно представить как
![]()
(16.9)
где Р0, ρ0 и с0 — соответственно давление, плотность натрия и скорость звука в неподвижном натрии.
Затем натрий над зоной взаимодействия движется вверх как несжимаемая инерционная масса. На этом этапе расширение натрия сдерживается за счет сил инерции. Следовательно, зависимость давления от скорости движения натрия получается из уравнения F =ma и имеет вид:
![]()
(16.10)
где H — высота столба натрия над зоной взаимодействия; Р0 — давление защитного газа в реакторе; g — ускорение свободного падения.
Расчетная модель SOCOOL
Оценка уменьшения расчетного количества выделяемой механической энергии за счет нестационарных процессов теплопереноса и механических сдерживающих факторов была впервые сделана Падиллой [5]. В использованной им расчетной модели SOCOOL предполагалось, что первый этап расширения длится до возвращения в зону взаимодействия волны давления после достижения ею верхней кромки массы натрия. Этот этап называется периодом разгрузки. Считается, что до начала периода разгрузки тепло от поверхности капель топлива свободно передается натрию, однако учитывалась низкая теплопроводность оксидного топлива путем ввода в программу уравнений нестационарного процесса теплопереноса внутри сферической капли топлива. После завершения периода разгрузки капля топлива окружена оболочкой натриевых паров, и теплообмен топлива с натрием резко уменьшается. Поэтому количество совершенной натрием работы рассчитывается из уравнения термодинамического, не зависящего от времени, процесса расширения. Для данной расчетной модели уравнение первого закона термодинамики в производных по времени имеет вид:
![]() (16.11)
(16.11)
где Q — скорость переноса тепла от топлива к натрию.
Скорость теплопереноса и совершенная механическая работа, рассчитываемые по программе SOCOOL, зависят от размеров капель топлива. Для выполнения условий теплового равновесия (как это принято в модели Хикса—Мензиса) необходимо, чтобы капли топлива обладали нулевым объемом. Результаты экспериментальных исследований показывают, что средний диаметр частиц UO2 при смешивании топлива с натрием составляет от 100 до 1000 мкм (см. рис. 16.9). Для таких размеров частиц расчетное значение выделяемой механической энергии значительно меньше, чем в условиях термического равновесия. Нельзя не учитывать также наличие частиц топлива меньших размеров, поскольку существует вероятность появления детонационной волны, о чем будет сказано ниже, при рассмотрении расчетной модели процесса, предложенной Бордом и Холлом.
Параметрическая модель процесса
Чо и Райт предложили более общий вариант модели Падиллы [6]. Во-первых, ими было введено обобщенное описание сдерживающих факторов в зоне взаимодействия расплавленного топлива с натрием (звуковая волна и силы инерции). Кроме того, были уточнены уравнения теплопереноса, а также введена постоянная времени, позволяющая учесть задержку процесса расширения за счет дробления топлива и смешивания его с натрием. Введение этих модификаций в программу привело к дальнейшему уменьшению расчетного значения выделяемой механической энергии. Дополнительные усовершенствования коснулись параметрических моделей.
Основной трудностью, связанной с применением параметрических расчетных моделей переходных процессов, было отсутствие экспериментальных данных, необходимых для сравнения с результатами расчета. Только в конце 70-х годов Якобс (Карлсруэ, ФРГ) разработал расчетную программу MURTI параметрического типа [7]. Результаты расчетов процесса взаимодействия расплавленной UO2 с натрием сравнивались с данными экспериментальных исследований, проведенных в Центре ядерных исследований в Гренобле и в Лаборатории в Сэндиа [9].

