Для оценки количества механической работы, совершенной в процессе расширения топлива, используются два метода. Первый из них — метод предельной оценки, предполагает расчет максимально возможного значения энергии, которая передается стенкам корпуса реактора. Второй метод — детерминистический, который учитывает потери энергии в элементах конструкции реактора.
А. МЕТОД ПРЕДЕЛЬНОЙ ОЦЕНКИ ВЫДЕЛЯЕМОЙ ЭНЕРГИИ
Одним из способов оценки механической энергии, передаваемой стенкам бака, является расчет величины PdV, т. е. энергии, выделяемой при расширении топлива, находящегося в двухфазном состоянии, до достижения в системе конечного давления. Для определения максимально возможного количества выделяющейся энергии задают значение конечного давления, равное 1 ат, хотя в действительности давление внутри корпуса реактора после расширения топлива будет существенно выше.
Теоретически возможное значение энергии, выделяемой при расширении испаряющегося топлива, можно оценить, рассмотрев процесс на Т — s-диаграмме для топлива (рис. 16.2). За исходное состояние системы принимаем стационарный номинальный режим активной зоны; при этом топливо находится в твердой фазе и существует его равновесие с парами при данной температуре (точка 1 на диаграмме).
Аварийный процесс начинается с вводом реактивности в активную зону, что вызывает рост мощности и температуры (линия 1— 2). Участок 2—3 соответствует процессу плавления топлива. Дальнейшее увеличение мощности приводит к росту температуры топлива, начинается его испарение, и под действием растущего давления активная зона разрушается. Когда мощность активной зоны достигает максимального значения, точка, характеризующая состояние топлива на диаграмме, очевидно, будет незначительно ниже линии насыщения (так как количество вещества и объем расширения невелики). Согласно другой теории топливо может находиться в жидкой фазе, если, расширяясь, заполнит весь объем активной зоны (см. § 15.7).
В расчетах чаще всего рассматривается первый вариант. Поэтому на рис. 16.2 состояние топлива в момент достижения максимальной мощности изображено точкой 4.
Предполагается, что вслед за этим происходит адиабатическое расширение топлива (обратимый процесс при постоянном значении энтропии, обозначенный отрезком 4—5), в результате которого высвобождается механическая энергия, а давление в активной зоне падает. Расплавленная масса активной зоны, расширяясь и разрушая внутренние конструкции, увеличит давление на стенки бака и трубопроводов первого контура.

Рис. 16.2. Процесс разрушения активной зоны, изображенный в Т — s-диаграмме для топлива Температура плавления топлива (UO2—PuO2) Tпл =3040 К, температура насыщения при атмосферном давлении равна приблизительно 3500 К; критическая температура Ткр=8000 К
I — твердое топливо; II — твердое н жидкое топливо; III- жидкая фаза; IV — жидкость и пар; V—пар; VI — твердое топливо и пар, а -завершающая стадия разрушения активной зоны; б — процесс адиабатического расширения
Натрий, находящийся над активной зоной, под действием давления топлива поднимается до верхней крышки бака, тем самым нагружая ее дополнительными внутренними усилиями. Более подробно эти процессы обсуждаются в § 16.4. Расширение будет продолжаться до того момента, когда уровень натрия достигнет крышки реактора, а активная зона займет все пространство, ограниченное натрием и стенками бака (точка 5 на рисунке). Работа, совершенная в процессе расширения топлива, может быть рассчитана из уравнения первого закона термодинамики, записанного для заданного количества топлива в двухфазном состоянии:
![]() (16.1)
(16.1)
где dQ — количество тепла, отведенного от топлива в процессе расширения; dU — изменение внутренней энергии; dW — энергия, сообщаемая топливом окружающим его объектам (т. е. натрию и стенкам бака). Если предположить, что процесс расширения — адиабатический, тогда dQ = 0, а расчетное значение энергии будет максимально возможным при расширении топлива. При таком допущении получим
![]() (16.2)
(16.2)
В процессе расчета обычно известен какой-либо термодинамический параметр состояния системы в точке 5: давление Р5 или удельный объем υ5, рассчитываемый для данного объема контура. Параметры топлива (U4 и удельная энтропия s4) в конце процесса расширения определяются расчетным путем. Используя величину s4 (которая равна s5), а также Р5 или υ5 из уравнения состояния топлива, можно получить конечное значение внутренней энергии U5. Таким образом, теперь можно рассчитать совершенную топливом работу.
Из уравнения (16.2) можно получить другое выражение для Wмакс используя параметры, которые рассчитываются проще, чем U4 и U5, при следующих допущениях: пары топлива рассматриваются как идеальный газ;
скрытая теплота парообразования топлива имеет постоянное значение; удельный объем жидкого топлива значительно меньше, чем удельный объем его паров; удельная теплоемкость расплавленного топлива — постоянная величина. Уравнение имеет следующий вид;
![]() (16.3)
(16.3)
где Mf — количество топлива в процессе расширения, кг; ср — удельная теплоемкость жидкого топлива, Дж/(кг · К); hfg — скрытая теплота парообразования, Дж/кг; х — степень сухости пара; R — газовая постоянная паров топлива [для UO2 — PuO2 R = 8317/270 Дж/(кг · К)].
Степень сухости в точке 4 определяется выражением
![]() (16.4)
(16.4)
где V4 — объем, который занимает количество топлива Mf в момент, предшествующий расширению; v — удельные объемы насыщенного пара (vg) и жидкости (vl) при температуре Т4.
Степень сухости в точке 5 определяется выражением
![]() (16.5)
(16.5)
Если известно Р5, из уравнения состояния газа (15.23) можно найти T5. Затем рассчитывается х5 и, наконец, Wмакс. Если для конечного состояния процесса (точка 5) известен объем V5, а давление Р5 не известно, задача усложняется. Пренебрегая величиной vl и полагая vg5 — RT5/P5 (как для идеального газа), получаем
![]()
Выражая отсюда xs и подставляя это выражение в (16.5), находим
![]() (16.6)
(16.6)
где Р5 (Т5) определяется из уравнения (15.23). Это уравнение решается относительно Т5, чтобы найти х5, а затем Wмакс.
Необходимо рассмотреть еще одну особенность процесса расширения топлива. Уравнения (16.2)—(16.6) составлены исходя из условия, что в точках 4 и 5 процесса температурное поле активной зоны однородно, т. е. вся масса активной зоны имеет одинаковую температуру. Однако в действительности температура в центре активной зоны выше, чем на периферии. Если представить, что расширение ячеек активной зоны происходит независимо друг от друга, совершенная работа будет значительно больше, чем в том случае, когда перед началом расширения температура в активной зоне выравнивается за счет теплообмена и перемешивания топлива. В статье [11 приводятся результаты количественных оценок этого эффекта. Различие значений механической энергии объясняется тем, что выравнивание температуры топлива — это необратимый процесс, в результате которого потенциальная энергия массы топлива уменьшается. Такое выравнивание, предшествующее процессу расширения (или происходящее одновременно с расширением), называют самоперемешиванием. Если в уравнении (16.3) используется среднее значение температуры в активной зоне, расчетное значение выделяющейся энергии будет низким.
Б. ДЕТЕРМИНИСТИЧЕСКИЙ МЕТОД РАСЧЕТА ВЫДЕЛЯЕМОЙ ЭНЕРГИИ
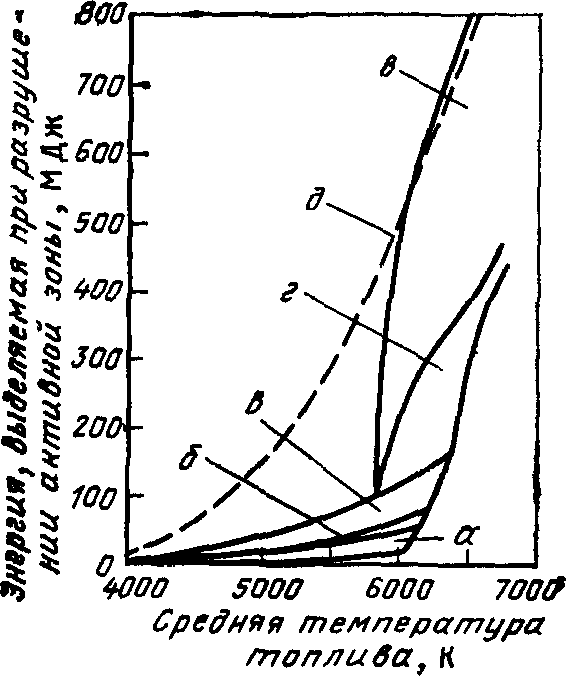
Рис. 16.3 Влияние детерминистического подхода и различных вариантов исходных данных на результаты расчета количества энергии, выделяемой в процессе разрушения активной зоны: а - зависимость результатов от используемых расчетных моделей, б — различный характер распределения массы натрия в реакторном баке, в — эффект перемешивания топлива с натрием; г — возможные повреждения верхних элементов активной зоны и внутриреакторных конструкций, д — энергия, выделяемая в процессе адиабатического расширения топлива
Действительный процесс увеличения объема топливной массы при гипотетической аварии разрушения активной зоны реактора с жидкометаллическим теплоносителем сопровождается явлениями, которые существенно снижают величину выделяемой энергии. К ним относятся, например, тепловые и механические потери на прилегающих к активной зоне элементах конструкции. За счет самоперемешивания топлива и градиентов давления в жидком топливе возникают дополнительные потери в процессе преобразования тепловой энергии в механическую.
Кроме того, конечное значение энергии снижается в результате местных гидравлических потерь потока, обусловленных сложной геометрией
внутриреакторных конструкций. Верхние части тепловыделяющих сборок, включающие в себя газовую полость и зону воспроизводства, частично гасят энергию расширяющейся топливной массы.
Первые расчеты режима расширения топлива и сопровождающих его гидродинамических процессов в двухмерной геометрии выполнялись по программам REXCO и ICECO1. Экспериментальные исследования проводились в США и в европейских странах как на стендах, так и на реакторах: TREAT (Аргоннская национальная лаборатория, Айдахо Фоллз), ACPR (Сэндиа, Альбукерке) и CABRI (Центр ядерных исследований, Кадараш).
Наиболее совершенной программой является SIMMER, которая описана в § 15.6. Первые расчеты, проведенные по этой программе, показали, что факторы, о которых говорилось выше, снижают на порядок значение энергии, передаваемой на стенки бака реактора. На рис. 16.3 представлены результаты расчетов гипотетической аварии реактора с жидкометаллическим теплоносителем по программе SIMMER; для сравнения приведены данные, полученные по методу предельной оценки (при адиабатическом расширении топлива). Приведена также зависимость выделяющейся энергии от средней температуры топлива на последней стадии разрушения активной зоны. Нижние кривые показывают изменение значений энергии, рассчитанных по программе SIMMER, за счет упомянутых выше явлений. Над ними расположена область, характеризующая изменение значения механической энергии за счет взаимодействия топлива с натрием и испарения теплоносителя.
Расчеты показывают, что при средней температуре топлива, не превышающей 6000 К, выход энергии значительно меньше, чем в случае адиабатического процесса расширения. Это может быть учтено при разработке проекта активной зоны.
1 Программы типов REXCO и ICECO описаны в § 16 4.

