7.9. Применение вычислительного эксперимента для анализа результатов испытаний термоэмиссионных электрогенерирующих сборок
Одним из эффективных средств изучения физических явлений и процессов в сложных технических объектах, к которым относятся и термоэмиссионные ЭГС, является вычислительный эксперимент. Применение вычислительного эксперимента на этапе проектирования позволяет сократить материальные затраты за счет выбора оптимальной конструкции на основе проведения многовариантных расчетов. Велика роль такого эксперимента и при испытаниях ЭГС, когда информация о внутренних параметрах ЭГС, как правило, определяется косвенными методами на основе измерения ограниченного числа параметров. Практически лишь с привлечением вычислительного эксперимента удавалось получить количественную информацию при регистрации аномальных характеристик.
В настоящее время накоплен достаточно успешный опыт использования вычислительного эксперимента при проведении петлевых испытаний ЭГС [44, 46, 107, 270, 274—276]. Для проведения вычислительного эксперимента необходимы математическая модель (ММ) ЭГС для разных режимов работы, алгоритмы решения различных задач и пакет прикладных программ, реализованный на ЭВМ. При моделировании характеристик ЭГС принимаются определенные допущения, которые позволяют обобщенную модель ЭГС разбить на ряд частных моделей, описывающих эмиссионно-адсорбционные, плазменные, тепловые, электрические и другие процессы. Все частные модели процессов в ЭГС можно условно разбить на два уровня. К первому относятся модели эмиссионно-адсорбционных и плазменных процессов в ЭГС. Математические модели этого уровня представляют собой системы уравнений, описывающие процессы прохождения тока через цезиевую плазму [61, 62, 277—280]. Результатом работы![]() этих моделей являются серии МЭЗ; pCs — давление пара цезия; υ — напряжение между электродами, TCs — температура цезиевого термостата.
этих моделей являются серии МЭЗ; pCs — давление пара цезия; υ — напряжение между электродами, TCs — температура цезиевого термостата.
Второй уровень состоит из моделей тепловых, электрических, гидравлических, магнитных и т. п. процессов, учитывающих конкретную геометрию и неоднородность распределения внутренних параметров вдоль ЭГС [281—283]. Применительно к рассматриваемой задаче использования ММ при петлевых испытаниях дополнительно особое внимание должно уделяться моделированию нерасчетных и аварийных режимов работы, например, связанных с утечками тепла и тока между электродами и элементами, пробоя коллекторной изоляции, образования «ложного» термостата и т. п. Основным результатом работы моделей второго уровня являются интегральные ВАХ ЭГС, температурные и электрические поля, поля давлений рабочего тела и откачиваемых газов и т. п. для различных режимов работы.
Реализованное в [272, 283] представление полной ММ ЭГС в виде двух уровней частных моделей позволило упростить и ускорить процесс моделирования характеристик ЭГС при проведении вычислительного эксперимента, так как зависимости, используемые в моделях второго вида, при развитом банке данных могут быть получены предварительно. Кроме того, разбиение модели ЭГС на ряд частных случаев позволяет использовать эффективные численные алгоритмы при решении обыкновенных дифференциальных уравнений, уравнений в частных произвольных и нелинейных алгебраических уравнений, описывающих соответствующие процессы. Алгоритмы численного моделирования характеристик ЭГС основаны, как правило, на использовании теории конечных разностей и реализованы в виде отдельных программ.
Накопленный опыт работы с программами комплекса позволяет выделить в качестве типовых следующие задачи:
расчет изотермических ВАХ точечного ТЭП в вакуумном, диффузионном и разрядном режимах работы;
расчет температурных полей ЭГС;
расчет электрических полей ЭГС;
расчет распределения давления пара цезия по тракту подачи и в самой ЭГС;
расчет ВАХ ЭГС в вакуумном, диффузионном, разрядном и переходном от диффузионного к разрядному режиму;
определение внутренних параметров ЭГС по экспериментальным ВАХ в различных режимах работы;
моделирование аномальных явлений, предполагаемых причин отказов.
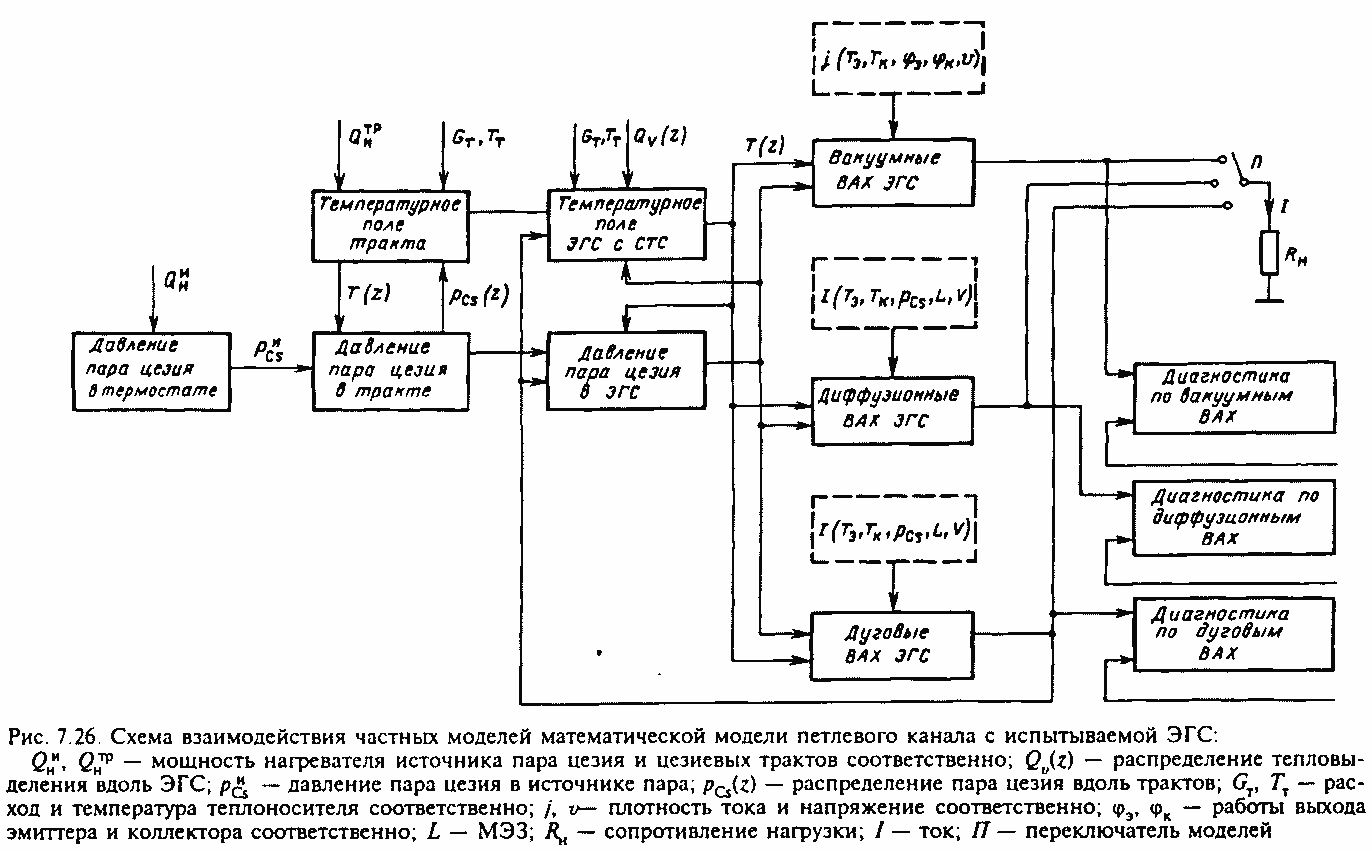
Для решения каждой типовой задачи разработаны отдельные программы, называемые функциональными модулями. Каждый модуль имеет внешние управляющие параметры и выходные характеристики. Взаимный обмен между модулями информацией осуществляется через банк данных. На основе использования специальных программных средств формируется список функциональных модулей и программ общего пользования, необходимых для решения конкретной задачи. Типовой модуль формируется в ЭВМ с помощью запускающей программы, в которой задаются соответствующие управляющие параметры и условия обмена с банком данных числовой информацией. Управление комплексом программ производится с помощью диалоговой системы. В качестве иллюстрации работы с комплексом программ на рис. 7.26 представлена схема взаимодействия модулей, запускающих программ и банка данных при моделировании ВАХ ЭГС в составе ПК или ТРП.
Необходимо отметить, что модульная структура построения комплекса программ позволяет проводить модернизацию отдельных модулей, их замену, подключение новых модулей, формирование расчетных путей и т. п.
Алгоритм вычислительного эксперимента. Собственно вычислительный эксперимент начинается после отладки и тестирования отдельных модулей комплекса программ и состоит из следующих этапов:
- Определяются условия работы испытываемой (или проектируемой) ЭГС и выбирается набор функциональных модулей, необходимых для решения задачи.
- Проводится настройка модели на объект исследования путем задания исходных данных (геометрических размеров, теплофизических свойств материалов, эмиссионных характеристик электродов и т.п.). Часть исходной информации по испытываемой ЭГС может быть оценена с помощью модулей диагностики ЭГС по экспериментальным данным.
- Задаются внешние воздействия на модель, аналогичные экспериментальным, например, профиль и уровень тепловыделения в сердечниках ЭГС, давление (температура) источника пара цезия, закон изменения нагрузки.
- Проводится математическое моделирование на ЭВМ рассматриваемых процессов путем запуска соответствующих программ.
- Сравниваются расчетные и экспериментальные характеристики ЭГС, проводится их анализ и разрабатываются предположения о возможных причинах их несоответствия.
- Проводится коррекция либо расчетной схемы, либо исходных данных.
- Определяется программа повторных численных экспериментов.
- В некоторых случаях разрабатываются рекомендации по проведению целенаправленных экспериментов при осуществлении соответствующего этапа испытаний ЭГС как для уточнения модели, так и для обеспечения более надежной идентификации обнаруженных аномалий. Одновременно может быть выполнено и обоснование безопасности проведения намечаемых экспериментов.
Рассмотренная технология вычислительного эксперимента, разработанная Ю.В. Бабушкиным, широко использовалась при проведении испытаний энергонапряженных ЭГС по программе РКК «Энергия» на реакторе ВВР-К, на котором был внедрен рассмотренный комплекс и создана АСНИ при проведении петлевых испытаний [46, 283, 284].
В качестве примера рассмотрим эффективность использования численного эксперимента для анализа гистерезисных статических ВАХ, причины образования которых непосредственно по результатам испытаний выяснить не удалось.
Качественное и количественное совпадения результатов вычислительного эксперимента с данными испытаний подтвердило, что ухудшение характеристик было связано с возникновением тепловых и электрических утечек по конденсату топлива между электродами ЭГЭ. Гистерезисный характер ВАХ, полученный в результате вычислительного эксперимента, подтвердил гипотезу о замыкании электродов при низких температурах эмиттеров (область короткого замыкания) и размыкании при высоких температурах (область холостого хода). Послереакторные исследования этой ЭГС показали наличие участков в МЭЗ с аномально высоким выносом оксида урана. Кроме интегральных характеристик, моделирование позволило во всех точках ВАХ получить информацию о температурных полях ЭГС, распределении токов и напряжений.
Диагностика на основе идентификации математических моделей
Применительно к наземным ядерно-энергетическим испытаниям космических ЯЭУ «Топаз» и «Топаз-2» в ГНЦ РФ ФЭИ и РНЦ «Курчатовский институт» были разработаны и успешно применялись методы диагностики испытываемых ЯЭУ на основе идентификации их математических моделей [45, 274, 275]. В принципе подобный подход может быть использован и при проведении петлевых испытаний ЭГС, и в особенности ЭГП из нескольких ЭГС.
Задача идентификации определяется как задача восстановления (уточнения) структуры известной теоретической ММ и ее внутренних непосредственно неизмеряемых параметров по внешним измеряемым при испытаниях параметрам Постоянное слежение в ходе испытаний за изменением внутренних параметров на основе идентификации, и интерпретация этих изменений являются наиболее эффективными способами диагностики сложных объектов.
Приступая к исследованию объекта испытаний, исследователь использует априорную теоретическую ММ (подходы к разработке которой могут быть различными) в качестве первой либо пробной модели и стремится прежде всего ответить на вопрос: учитывает ли ММ все связи, проявляющиеся в реальном объекте, и справедливы ли вносимые упрощения. При решении задачи структурной и параметрической идентификации важно, чтобы форма (структура) модели и по учету причинно-следственных связей, и по пространственной распределенности соответствовала содержанию экспериментальной информации. Предполагается, что сбор, обработка информации с датчиков и информационная поддержка оператора и исследователей осуществляются АСНИ и существует возможность реализации различных режимов испытаний. Способ решения задачи идентификации состоит в осуществлении минимизации невязки между экспериментальной и расчетной информациями с помощью одного из методов оптимизации. Отметим кажущийся парадокс: применительно к ТРП (или ЯЭУ) в условиях измерения только интегральных параметров по току и напряжению использование распределенной ММ для идентификации и диагностики теряет смысл и для описания ЭГС можно принять в качестве априорной теоретическую ММ в сосредоточенных параметрах. Однако в результате решения задачи идентификации с использованием ММ с сосредоточенными параметрами восстанавливаемые параметры являются характеристиками распределенной модели [45].
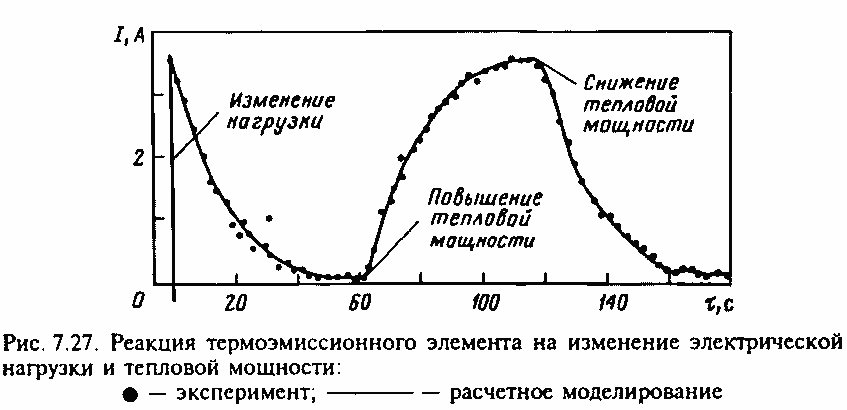
Представляет интерес решение задачи идентификации в рамках линейной модели статики, которое позволило получить аналитические выражения для ряда непосредственно неизменяемых параметров через измеряемые параметры [45]. План такого эксперимента (изменение тепловой мощности и сопротивления нагрузки) приведен на рис. 7.27.

