Если рассмотреть распределение затрат во времени по крупному объекту, то для начального периода строительства годовые затраты Зt=Kt, а после окончания строительства в процессе эксплуатации. В общем случае, когда строительство еще не завершено, а эксплуатация уже начата, Зt=Kt+Иt.
Прямое суммирование годовых капитальных вложений и издержек производства основано на тезисе о равенстве рубля капитальных вложений и рубля текущих издержек, высказанном и рассмотренном в [7, 25]. Такое суммирование не означает смешения понятий капитальных вложений и текущих издержек, хотя и разделение этих понятий также часто является условным. Так, составляющая амортизации, направляемая на капитальный ремонт, может трактоваться двояко. По источнику образования — это издержки производства, а по направлению использования — капитальные вложения, так как результатом капитального ремонта является обновление элементов основных фондов.
В рассматриваемом случае суммирование капитальных вложений и издержек производства выполняет лишь функцию учета затрат, a Kt и Ht принимаются в соответствии с конкретными показателями каждого сравниваемого варианта. При этом необходим учет затрат за весь период. Однако непосредственно складывать затраты разных лет нельзя, так как средства, израсходованные в разные годы, неравноценны между собой. Покажем это на примере.
Допустим, имеются три варианта развития объекта, которые отличаются один от другого только тем, что часть затрат осуществляется в разные годы. Все остальные технико-экономические показатели у всех вариантов одинаковы и поэтому не влияют на их сравнительную экономичность, а следовательно, могут не рассматриваться. Графики затрат, различающихся по времени, представлены на рис. 1.1.
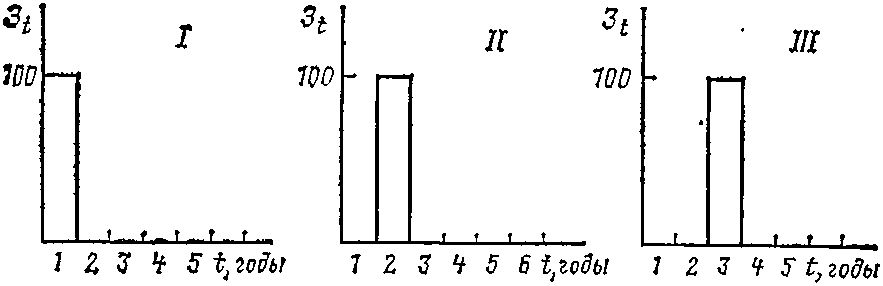
Рис. 1.1. Распределение затрат во времени по вариантам строительства второй очереди объекта
Рассматриваемый (или близкий к нему) случай может быть, когда сооружается, например, двухцепная линия электропередачи. Если в первые 3 года ее эксплуатации нагрузка мала даже по отношению к пропускной способности одной цепи, а в 4-м году она резко увеличивается и требуется одновременное использование обеих цепей, то номинальные (сметные) затраты, связанные с сооружением второй цепи, можно принять не зависящими от того, когда осуществляется это сооружение: в 1, 2 или 3-м году. В результате варианты различаются лишь распределением капитальных вложений во времени.
Из сравнения вариантов по сметным затратам нельзя сделать вывода о явных преимуществах какого-либо из вариантов на рис. 1.1. Можно лишь отметить, что исходя из разумных предпосылок следует отдать предпочтение варианту III, так как в более раннем вложении средств (варианты I и II) производственной необходимости не имеется. Однако если бы варианты различались также по номинальным (сметным) затратам и более раннее вложение средств позволило уменьшить сметные затраты, то предсказать заранее ответ было бы невозможно.
Приведенный пример позволяет в «чистом» виде оценить неравноценность разновременных затрат. Для этого рассмотрим сначала отличие варианта II от варианта III. В варианте II затраты осуществляются на 1 год раньше и в течение этого года не используются для выпуска продукции. Они оказываются изъятыми из народнохозяйственного оборота. Использование этих средств на других участках народного хозяйства позволило бы получать относительную годовую прибыль. В данном рассуждении иногда пытаются обнаружить парадокс, указывая на то, что и при использовании на других участках народного хозяйства деньги будут расходоваться в первую очередь для строительства и также окажутся «замороженными». Однако этот парадокс мнимый. Направление высвобожденных на рассматриваемом объекте средств на строительство другого объекта означает, что может быть увеличен общий объем капитального строительства в период между вводом в строй первой очереди рассматриваемого объекта и сооружением второй очереди. Если не перераспределять капитальные вложения во времени на данном объекте и не направлять их на другие объекты, то для увеличения общего объема капитального строительства потребовалось бы дополнительное финансирование. Отсюда следует, что сдвиг затрат во времени на более поздний срок равноценен получению дополнительной прибыли, и, наоборот, более раннее вложение средств без отдачи означает потерю возможности получения прибыли.
Таким образом, осуществление варианта II вместо варианта III наносит народному хозяйству ущерб, с учетом которого приведенные затраты по варианту II
где Зн — номинальные (сметные) затраты по варианту II; р— норматив приведения затрат.
В варианте I по сравнению с вариантом III затраты «замораживаются» на 2 года. Приведенные затраты по этому варианту 
Здесь учитывается, что во 2-м году наносится ущерб народному хозяйству не только от отвлечения номинальных (сметных) затрат, но и от потерянной прибыли 1-го года.
Таким образом, в основу расчета приведенных величин, учитывающих неравноценность разновременных затрат, положен закон сложных процентов. Допустим для примера, что номинальные (сметные) затраты равны 100 тыс. руб., а р = 0,12.
Тогда для варианта III, по отношению к которому рассматриваем ЗIII=ЗIII = 100 тыс. руб. В варианте II: ЗII= 100·1,12= 112 тыс. руб.; в варианте I: ЗI= 100·1,122=125,44 тыс. руб. Эти результаты дают возможность количественно оценить неравноценность разновременных затрат.
Все рассуждения вели до сих пор по отношению к варианту III, для которого принимали равенство приведенных затрат номинальным (сметным). Однако рассмотрение можно вести и по отношению к любому другому варианту, допустим, к варианту I, приняв ЗI=ЗI. При этом переход к варианту II будет означать, что на год высвобождаются затраты, которые дадут на других участках народного хозяйства дополнительную прибыль. На следующий год ее можно использовать для финансирования варианта II. Тогда ЗII=ЗII/(1+р).
В варианте III по сравнению с вариантом I затраты высвобождаются на 2 года. Поэтому ЗIII=ЗIII/(1+р)2.
Подставив численные значения, получим:
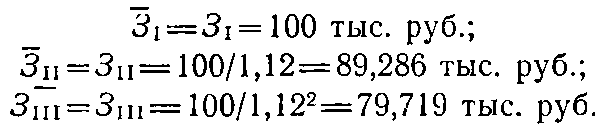
В данном случае получили иные приведенные затраты. Так, в варианте I — 100 тыс. руб. вместо 125,44 тыс. руб., в варианте II 89,286 тыс. руб. вместо 112 тыс. руб. Однако, соотношения приведенных затрат по сравниваемым вариантам при этом не изменились, так как ЗI/ЗII=125,44/112= 100/89,288=1,12.
Следовательно, в обоих случаях минимум приведенных затрат сохраняется за одним и тем же вариантом. Различие же в приведенных затратах объясняется тем, что в первом случае все затраты приводились к 3-му году, а во втором — к 1-му году.
Если обозначим год, к которому приводятся затраты, через τ и возьмем номинальные (сметные) затраты Зt для некоторого произвольного года, то
(1-1).
где 
коэффициент разновременности затрат. Анализ формулы (1.1) показывает, что она характеризуется следующими свойствами:
- при τ>t показатель степени коэффициента разновременности затрат больше нуля и Зt>Зt;
- при τ<t имеем Зt<Зt;
- при τ=t получается
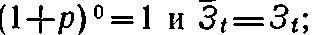
- при t→∞ коэффициент
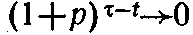и соответственно Зt→0.
Три первых свойства наглядно иллюстрируются рассмотренным выше примером, где номер варианта совпадает с годом затрат. В первом случае за базу принимали вариант III и τ=3, во втором случае — вариант I и τ=1.
Четвертое свойство указывает, что чем более отдалены затраты во времени, тем меньше их приведенные значения в расчете. Отсюда видно, что отдаление затрат выгодно для экономики страны, если при этом, конечно, не нарушаются планы развития народного хозяйства. Применительно к отдельным объектам или производственным системам это означает, что заведомо выгодным является отдаление тех или иных видов (либо составляющих) затрат при условии, что обеспечивается заданный производственный эффект. Сдвиг затрат на более поздние сроки равноценен увеличению ресурсов в период, когда эти затраты намечалось осуществлять по первоначальному варианту.
Выражение (1.1) можно представить в виде
Отсюда видно, что коэффициент (1+ρ)τ при заданном τ является постоянным множителем, изменяющим масштаб приведенных затрат. Если этот множитель одинаков для всех сравниваемых вариантов, то независимо от значения τ ранжироваться по затратам варианты будут одинаково. Следовательно, теоретически в расчетах можно принимать любое значение τ, и это не повлияет на выбор оптимального варианта, если для всех сравниваемых вариантов принято одно и то же значение τ.
В общем виде зависимость коэффициента разновременности от времени при р=0,12 и τ=0 показана на рис. 1.2. Высота ординаты каждой горизонтальной ступеньки отражает значение коэффициента приведения для соответствующего года. Такое графическое представление рассматриваемой зависимости соответствует годовой схеме учета затрат, которая широко используется в экономических расчетах. Это обусловлено тем, что финансирование народного хозяйства осуществляется в годовом разрезе.
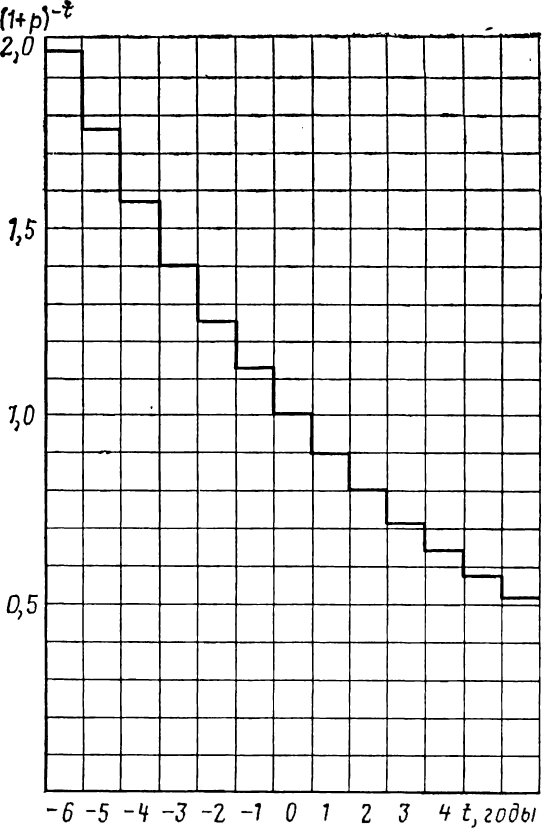
Рис. 1.2. Зависимость коэффициента разновременности затрат от времени
Основой в хозяйственной практике является и годовая отчетность.
Рассматриваемый закон приведения затрат характеризуется важным свойством, вытекающим из отношения приведенных затрат двух смежных лет. Так, для некоторого произвольного года t приведенные затраты определяются (1.1), а для следующего за ним года t+l
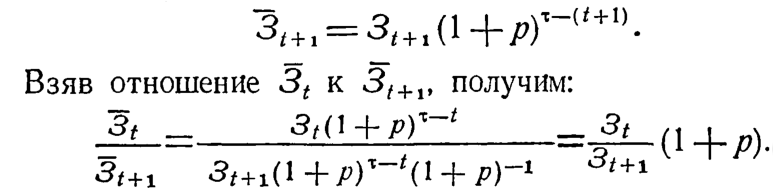
Если при этом 
Из последнего соотношения следует, что сдвиг затрат по времени на 1 год (на более ранний срок) равноценен их увеличению в 1+р раз. Эта кратность характерна для любых 2 смежных лет и не зависит от длительности периода, за который учитываются затраты.
Одним из первых, предложивших рассмотренный способ учета неравноценности затрат во времени, был А. Л. Лурье [41]. В конце 50-х годов этот способ был рекомендован для использования при сравнении вариантов в «Основных методических положениях техникоэкономических расчетов в энергетике» [59], а затем в первой Типовой методике [70]. В настоящее время учет неравноценности затрат по сложным процентам получил широкое распространение и используется во всех методиках технико-экономических расчетов.
Здесь не рассматриваются другие возможные или предложенные ранее способы соизмерения затрат во времени. Некоторые из этих способов проанализировал В. П. Браилов в [25]. Там же показано, что способ учета неравноценности затрат во времени по закону сложных процентов, т. е. по геометрической прогрессии, хорошо согласуется с общими зависимостями, отражающими характер экономического развития: изменением во времени производства валовой продукции промышленности, ростом стоимости основных производственных фондов.
Не нашел пока полного решения вопрос о размере норматива р. Строгого теоретического обоснования численного значения этого норматива пока не имеется. Поэтому р принимается различным в разных методиках. Норматив приведения в «Методике технико-экономических расчетов в энергетике» [49] принят равным 0,15. При этом и норму реновации рассчитывают с учетом фактора времени, в связи с чем она получается значительно меньше действующих (утвержденных) норм. В «Методике определения экономической эффективности использования в народном хозяйстве новой техники, изобретений и рационализаторских предложений» [46] норматив приведения принят равным 0,1 и норму реновации также рассчитывают с учетом фактора времени (§ 3.3). Однако коэффициент эффективности капитальных вложений предлагается принимать в 1,5 раза большим норматива приведения, т. е. равным 0,15. В Типовой методике [70] и ее последующей редакции [69] при действующем порядке определения норм реновации рекомендуется норматив приведения затрат в размере 0,08. Одновременно с этим предлагается принимать нормативный коэффициент эффективности капитальных вложений равным 0,12.
Аналогичные рекомендации содержатся и в отраслевой инструкции Минэнерго СССР [30], которая является основным методическим документом при обосновании плановых и проектных решений в энергетике.
В Инструкции по определению экономической эффективности капитальных вложений в строительстве (СН 423—71) для районов Крайнего Севера нормативный коэффициент эффективности капитальных вложений рекомендуется в размере 0,08. В [51] эта рекомендация распространена также на крупные комплексные гидроузлы, оказывающие влияние на формирование инфраструктуры района размещения ГЭС.
В энергетике многие специалисты склоняются к тому, что р=0,12. Это значение рекомендовано, например, бюро совета по комплексным проблемам энергетики (при отделении физико-технических проблем энергетики АН СССР) для проведения экономических сравнений вариантов в энергетике.
При выборе размера норматива приведения следует иметь в виду, что он используется в условиях единой социалистической экономики. Средства, высвобождающиеся в результате сдвига затрат во времени, должны быть использованы там, где это наиболее рационально для народного хозяйства. Следовательно, норматив приведения необходимо принимать единым для всех отраслей и тем более для всех типов задач. По нашему мнению, такая позиция теоретически наиболее правомерна, а р=0,12 соответствует требованиям настоящего времени и ближайшей перспективы.
Значение 0,12 корреспондирует с показателем прироста основных производственных фондов, т. е. с потребностями народного хозяйства в средствах, необходимых для осуществления процесса расширенного воспроизводства. Применительно к коэффициенту эффективности аналогичное толкование содержится в [76], где рассматривается связь между коэффициентом эффективности и долей национального дохода, направляемого на накопление.
Ниже в примерах и расчетах используется, как правило, р=0,12. Отдельные же зависимости рассматриваются также при значениях норматива приведения 0,08—0,1—0,12—0,15.
