Решения, принимаемые на основе сравнения вариантов по приведенным затратам и рентабельности, в ряде случаев не совпадают, на что неоднократно указывалось еще в 60-х годах Л. А. Ваагом. Тем не менее в типовой методике [69] и отраслевой инструкции [30] рекомендуются одновременно два критерия: минимум приведенных затрат и максимум рентабельности. В [25] сделана попытка рассмотреть условия, при которых решения по этим критериям получаются различными. В результате установлено, что существуют зоны несовпадения решений, однако, от каких факторов зависят и как изменяются размеры этих зон, до конца не было выяснено. Вместе с тем эти вопросы имеют большое практическое значение, так как в проектной и плановой практике используются оба критерия.
Сопоставление критериев минимума приведенных затрат и максимума рентабельности было затем выполнено В. П. Браиловым. Задачу он рассматривает применительно к оптимизации развития производственной системы и исследование проводит в координатах капиталовложения — издержки с помощью геометрических построений. Основной вывод, полученный в [6], заключается в том, что критерии минимума приведенных затрат и максимума рентабельности дают одинаковый результат при оптимизации, если выручка от реализации продукции равна минимальным приведенным затратам.
Излагаемый ниже подход дополняет выполненное В. П. Браиловым исследование, так как позволяет также проанализировать показатели зон несовпадения решений, получаемых по критериям минимума приведенных затрат и максимума рентабельности.
Для обобщенного решения поставленной задачи необходимо прежде всего найти выражение приведенных затрат, позволяющее представить в упорядоченном виде всю возможную совокупность их значений. Приведенные затраты З=ЕпК+И зависят от капитальных вложений и отношения издержек к капитальным вложениям.
Рис. 9.1. Характеристики зон несовпадения решений, получаемых при сравнении вариантов по приведенным затратам и рентабельности: а — частная характеристика; б — общая
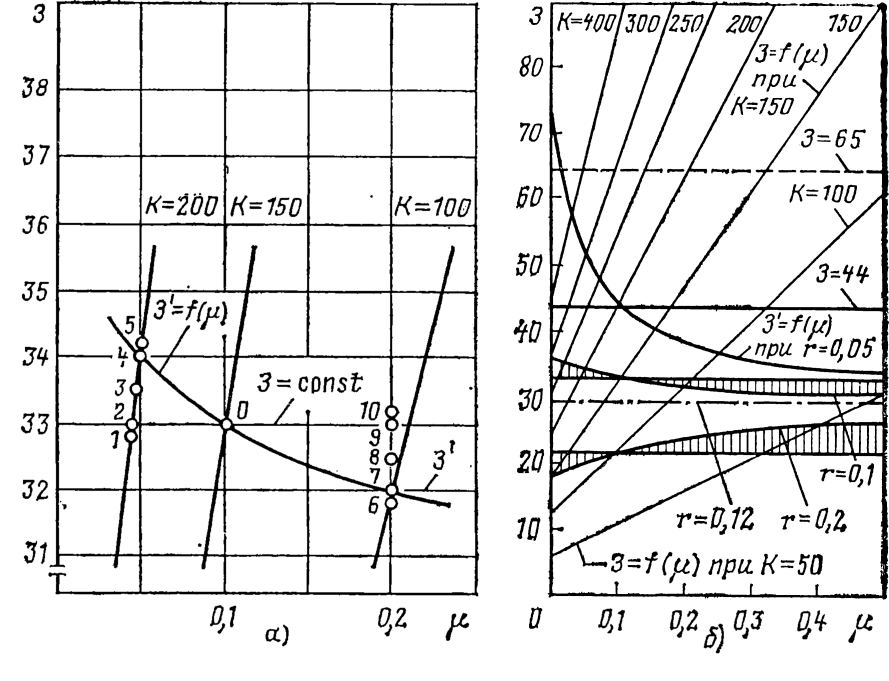
Если И/К обозначить через μ, то З=(Ен+μ)К. Уровень К удобно задавать в процентах, и тогда легко построить серию прямых З=f(μ) для различных значений К.
При этом для энергетических объектов характерны следующие значения:
![]()
Рассмотрим сначала ограниченную совокупность значений приведенных затрат в предложенной системе координат. На рис. 9.1,а представлены зависимости З=f(μ) для трех уровней капитальных затрат: 100, 150 и 200. Прямая З=const не зависит от μ, однако равноценные по приведенным затратам решения характеризуются при этом разной капиталоемкостью. Возьмем в качестве исходного (точка 0) решение с μ=0,1 и З=33, чему соответствует = 150. Рентабельность этого решения при цене Ц=30.
Если теперь найти все значения приведенных затрат З', при которых r=0,1, то получим кривую, характеризующую решения, равноценные по рентабельности. Построение этой кривой осуществляется следующим образом.
Из r=Ц/К —μ определим μ=(Ц/К) — r. При заданных Ц и r находим р для разных значений К. Затем для каждого сочетания μ и К рассчитываем З'. Так, при К= =200 μ=30/200—0,1=0,05 и З'= (0,05+0,12) 200=34, а при К= 100 μ=30/100—0,1 =0,2 и З'= (0,2+0,12)x100= 32.
Зависимости З=const и З'=f(μ) являются границами зон несовпадения решений по критериям минимума приведенных затрат и максимума рентабельности. Другими словами, любое решение в этих зонах при сравнении с исходными оказывается экономически оправданным по одному из критериев и неэффективным по другому критерию.
Общая характеристика зон расхождения результатов представлена на рис. 9.1,б. Кривые равнорентабельных решений
З'=f(μ) построены для r=0,05:0,1:0,12:0,2. Основные зоны расхождений рассматриваются применительно к случаям пересечения З и З' при μ=0,1, чему соответствуют З=44:33:30:22. Кроме того, для кривой З'=f(μ) при r=0,05 показаны также зоны расхождений для случая пересечения З и З' при μ=0,01 и соответственно З=65.
Как следует из рисунка, площадь зон расхождений зависит от кривизны 3'=f(μ), которая в свою очередь определяется рентабельностью исходного варианта r0. Если r мало отличается от Ен, то зоны расхождений относительно невелики. При r>Ен увеличение размеров зон расхождения с ростом r происходит медленно. Если же r<Ен, то с уменьшением r резко расширяются зоны расхождения результатов, что видно из рассмотрения кривой З'=f(μ) для r=0,05. Различие относительных зон расхождения при r>Ен и r<Ен подтверждается и специальным расчетом, выполненным для условия, когда r2=1,667Ен и r2=Ен/1,667.
Из рис. 9.1 следует, что при любых значениях r≠Ен имеются две зоны расхождения результатов, смыкающиеся в точке пересечения З=const и З'=f(μ). Для З'=f(μ) с заданной r площадь каждой зоны зависит от значения μ в исходном варианте.
На кривой с r=0,05 при исходном варианте с μ=0,1 (З=const показаны сплошной линией) площади расхождения решений в обеих зонах соизмеримы. Если же исходный вариант имеет μ= 0,01, то соотношение площадей зон резко изменяется.
Как отмечено выше, общая площадь зон расхождения результатов зависит от различия r и Ен. Если же исходный вариант характеризуется r=Ен, то любой другой неравноценный ему вариант отличается от него как по приведенным затратам, так и по рентабельности, т. е. решения по обоим критериям совпадают. В этом случае З'=f(μ) выражается прямой, сливающейся с З=const, так как цена и приведенные затраты совпадают. На рис. 9.1.б этот случай описывается штрих-пунктирной линией.
При анализе зон несовпадения решений важно отметить еще одну особенность, обусловленную характером кривизны. При r<Ен эта кривая обращена
выпуклостью вниз, а при r>Ен — выпуклостью вверх. В результате если вместо решения по минимуму приведенных затрат в зонах расхождения ориентироваться на максимум рентабельности, то это следующим образом повлияет на капиталоемкость:

Если имеется решение с r=Ен, то из возможных альтернативных вариантов в общем случае могут быть выделены две совокупности, для которых результаты сравнения с исходным вариантом по критериям минимума затрат и максимума рентабельности будут не совпадать.
Решение во всех случаях должно быть выбрано по критерию минимума приведенных затрат. Это обусловлено тем, что сравнение по приведенным затратам позволяет получить представление о народнохозяйственной эффективности вариантов. Рентабельность же отражает лишь отраслевую эффективность рассматриваемых вариантов. Разность между ценой и себестоимостью продукции по любому отдельно взятому решению—это прибыль, получаемая отраслью, размер которой непосредственно зависит от выбранного уровня цены. Поэтому и отношение прибыли к капитальным вложениям характеризует лишь отраслевую эффективность технического решения.
Расхождение решений, принимаемых по минимуму приведенных затрат и максимуму рентабельности, может получаться по двум причинам: во-первых, из-за различия нормативных рентабельности и коэффициента эффективности; во-вторых, когда цена связана с выбором решения, например при размещении электростанции в случае различия тарифов по энергосистемам.
Для анализа зон расхождения решений по рентабельности и приведенным затратам рассмотрим серию вариантов, представленных на рис. 9.1,а.
Таблица 9.5. Сравнение сходимости решений по минимуму приведенных затрат и максимуму рентабельности при r0<Ен
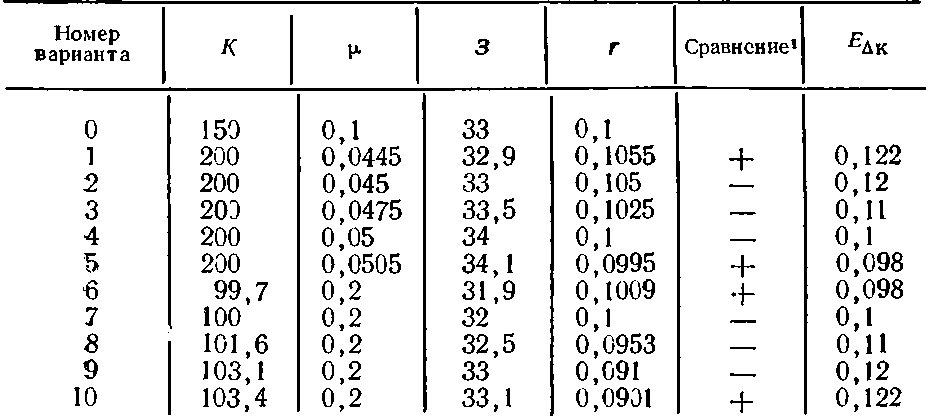
1 Знак плюс означает, что результаты сравнения решения в заданной точке с исходным вариантом получаются одинаковыми по обоим критериям; знак минус указывает на расхождение результатов.
Варианты 1—5 — это решения при K=const и μ=var, а варианты 6—10 относятся к решениям с μ=const и K=var. Каждый из этих вариантов сравнивается с исходным решением (точка 0). Количественная характеристика всех вариантов содержится в табл. 9.5, из которой видно, что совпадают результаты сравнения только по решениям, находящимся за пределами зон расхождения, т. е. по вариантам 1, 5, 6 и 10. По остальным вариантам, лежащим внутри и на границе зон, при сравнении их с исходным получаются различные решения по приведенным затратам и рентабельности.
В табл. 9.5 определены также коэффициенты эффективности дополнительных капитальных вложений ЕΔк, возникающих при переходе от нулевого варианта к любому другому. Так, переход к варианту З требует
ΔΚ=50, но приводит к уменьшению издержек ∆И=5,5, что обеспечивает ЕΔк= 0,11.
Рассмотрение показателей табл. 9.5 позволяет для случая r0<Ен сформировать условие, при котором результаты сравнения по приведенным затратам и рентабельности не совпадают:
![]() (9.15)
(9.15)
Нетрудно убедиться, что невыполнение хотя бы одного из неравенств означает совпадение результатов. Так, в варианте 5 Ен>ЕΔк, но ЕΔк<r0, а в варианте 10Eн<ЕΔк при ЕΔк>r0, что достаточно для расхождения решения.
Таблица 9.6. Сравнение сходимости решений по минимуму приведенных затрат и максимуму рентабельности при r0>Ен
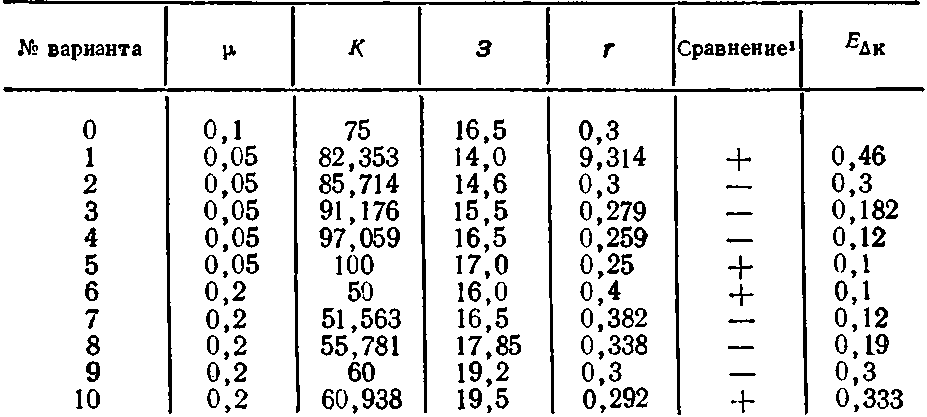
1 См. сноску к табл. 9.5.
При r0>Ен в условии, определяющем зоны расхождения результатов, меняются знаки неравенства, т. е. должно быть
![]()
(9.16)
В справедливости этого условия можно убедиться, если рассмотреть табл. 9.6, в которой расчеты выполнены для r0=0,3.
Необходимо отметить, что рассмотрение зон расхождения решений по критериям минимума приведенных затрат и максимума рентабельности выполнено на основе попарного сравнения вариантов относительно наперед заданного (произвольно выбранного) нулевого варианта. Если согласиться, что оптимальным является вариант с минимальными приведенными затратами и таким вариантом является нулевой, то по смыслу при r0<Ен на рис. 9.1,а и в табл. 9.5 выпадают из рассмотрения вариант 1 (точка 1) и вся правая зона расхождения решений.
В случае r0>EH из рассмотрения выпадает левая зона расхождения. При такой постановке в зону расхождений попадают все варианты, которые по максимуму рентабельности вступают в противоречие с оптимальным. Рентабельность (абсолютную эффективность) необходимо использовать только для ее сравнения с рентабельностью аналогичных действующих предприятий или с установленным нормативом с целью выявить влияние принимаемого решения на рентабельность отрасли.

