Системы тепловидения - Сокращенная система обозначений в фурье-анализе

3.6. Сокращенная система обозначений в фурье-анализе
Прежде чем обратиться к рассмотрению конкретных импульсных реакций и их преобразований полезно остановиться на системе обозначений в фурье-анализе. Во многих задачах для описания процессов формирования изображения в области частот используются ряды и интегралы Фурье, записанные в явной форме. К сожалению, такие соотношения часто трудно наглядно представить, с ними трудно манипулировать в сложных задачах, когда приходится свертывать или перемножать множество функций. Дело значительно упрощается, если использовать сокращенную систему обозначений, введенную Брейсуэллом [3] и Гудменом [1]. Эта система содержит два элемента — математические операторы и пары преобразований основных функций.
В предыдущих разделах было показано, что оператор двумерного преобразования Фурье определяется формулой

(3.26)
Свертка двух функций / {х, у) и g {х, у) обозначается f*g, где
(3.27)
Свертки применяются также к частотным функциям и обладают свойствами ассоциативности, коммутативности и дистрибутивности. Скалярное произведение обозначается знаком •, например f-g. Операции свертки и умножения представляют собой пары преобразований; таким образом,
(3.28)
Основные функции, применяемые в тепловидении, представлены на фиг. 3.12 в мнемоническом виде; даны их определения, графическое представление и преобразования Фурье. Для сохранения простоты обозначений фильтрующее свойство
г) Всякий раз, когда процесс получения изображения подвергается временной фильтрации, будем рассматривать только стационарные картины
и,   не оговаривая особо, производить преобразование координат в область пространственных частот, так что необходимо только двумерное преобразование.

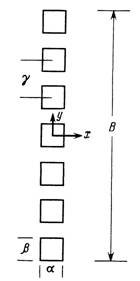
Фиг. 3.13. Линейка чувствительных элементов приемника излучения.

дельта-функции Дирака
(3.29)
представлено в виде
При использовании приведенных выше пар преобразований полученное выражение сводится к виду

Данный пример показывает порядок обычно проводимых манипуляции»
3.7. Оптические передаточные функции типичных элементов
Полезными аппроксимациями функций рассеяния, присущих обычным элементам систем изображения, являются следующие три функции. Это, во-первых, двумерная прямоугольная функция [Rect (#/a)-Rect (z//|3)], профиль которой по оси х показан на фиг. 3.14. В первом приближении можно полагать, что такую пространственную импульсную реакцию имеют чувствительные элементы прямоугольной формы. В действительности чувствительность приемника излучения может описываться далеко не прямоугольной функцией, однако точно контролировать форму функции при изготовлении приемника обычно не представляется возможным и большей частью принимают указанное первое приближение.
Если сканирование производится только в направлении х, то ОПФ приемника излучения есть преобразование Rect (х/а)
Таблица 3.1

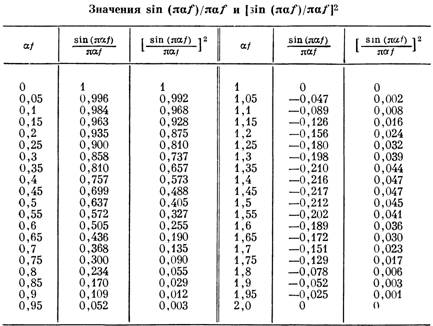
Фиг. 3.14. Профиль пространственной импульсной реакции прямоугольного приемника излучения.

и является действительной функцией вида
(3.31)
Значения этой функции и ее квадрата приведены в табл. 3.1 и представлены графически на фиг. 3.15. Прямоугольная функция может также описывать прямоугольные элементы индикаторных устройств, например светодиоды или ячейки газоразрядных индикаторных панелей.
Вторая употребительная функция рассеяния — двумерное гауссово распределение; в простейшем случае это гауссоида с круговой симметрией, сечение которой по оси х показано на фиг. 3.16. Функция рассеяния имеет следующий вид:
(3.32)

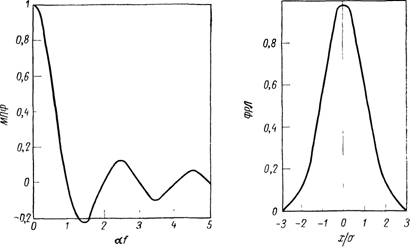
Фиг. 3.15. МПФ в виде Sinc-функции.
Фиг. 3.16. Обобщенная ФРЛ в виде гауссоиды.

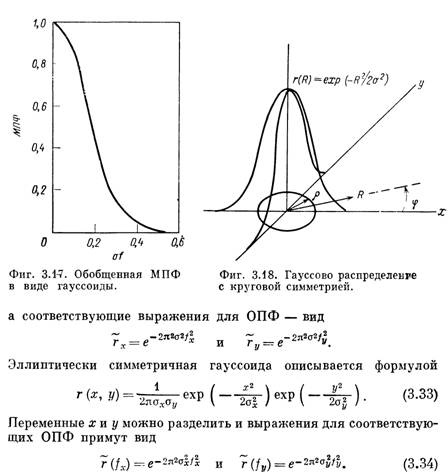
Нормированная МПФ в виде гауссоиды представлена на фиг. 3.17. В табл. 3.2 приведены три гауссоиды, причем значения а выражены в единицах углового размера приемника а, а частоты — в единицах /о = 1/а. Данные таблицы можно использовать для быстрой оценки влияния на МПФ приемника излучения видеоконтрольного устройства или других элементов системы, имеющих МПФ в виде гауссоиды.
Хотя импульсные реакции редко в точности описываются гауссоидой, часто бывает полезно аппроксимировать их гауссоидой. Например, размер пятна рассеяния оптики обычно характеризуют циаметром кружка 2р, в пределах которого заключен определенный процент полной энергии излучения. Если распределение энергии в пятне допустимо считать гауссовым, можно применить
Таблица 3.2
Значения МПФ элементов, имеющих гауссовы функции рассеяния. Величины а выражены в единицах углового размера приемника а.

и решая полученное уравнение относительно а, получаем
(3.36)
Таким образом, для гауссова пятна легко перейти от процентного содержания энергии Р в пределах заданного диаметра к среднеквадратичному отклонению а. Например, если 85% энергии заключено в кружке радиусом р, то а = 0,51р.                                                                                              $
Примерами явлений, импульсные реакции которых часто удовлетворительно описываются гауссоидой, являются симметричное аберрационное пятно оптической системы, случайные погрешности положения сканирующего устройства, вибрации чувствительного элемента, пятно на экране электронно-лучевой трубки. Шаде [34] привел множество практических примеров функций рассеяния электронно-лучевых трубок гауссова типа и их преобразований. Обычно подробные сведения такого рода у изготовителей электронно-лучевых трубок отсутствуют. Вместо этого размер пятна определяется по полусубъективным испытаниям, в ходе которых оценивается размер растра, воспринимаемый на пороге различения отдельных линий. При испытаниях размер растра плавно уменьшается электронным способом. В случае когда пятно представляет симметричную гауссоиду, величина а связана [35, 36] с расстояниями между центрами соседних строк s соотношением
а = 0,545.                                     (3.37)
Если разрешение оценивается по частоте прямоугольной миры, величина о связана с периодом миры р соотношением
о = 0,42р.                                        (3.38)
Дженнис и др. [35] рассчитали картину растрового фона, получающуюся в телевизионном растре из линий гауссовой формы. Они нашли, что для hi а = 0 -н 4 картина синусоидальна (h — расстояние между линиями, а — среднеквадратичное отклонение). Процентная глубина растрового фона £ зависимости от hlo показана на фиг. 3.19.
Третья употребительная функция рассеяния — круговая функция (фиг. 3.20), которая определяется уравнением
(3.39)
ОПФ является действительной функцией и имеет вид
(3.40)
где J1 — функция Бесселя первого рода первого порядка, a fR — пространственная частота в любом радиальном направлении; х — сечение круговой функции (3.40) — показано на фиг. 3.21.

Фиг. 3.20. Круговая функция

Фиг. 3.21. Усеченная Bessinc-функция.

Фиг. 3.19. Процентная глубина растрового фона для растра, построенного из линий, распределение яркости которых имеет гауссову форму, в зависимости от отношения расстояния между линиями h к величине а [35].

Круговая функция может описывать сильно расфокусированную оптику, приемник излучения круглой формы или круглый индикаторный элемент. Bessinc-функция достаточно точно аппроксимируется [30] формулой
(3.41)

3,3 Ухудшение модуляционной передаточной функции вследствие движения и неопределенности положения изображения

Помимо источников потерь разрешающей способности, рассмотренных в разд. 3.5, которые всегда существуют в системах тепловидения, имеются еще четыре источника, которые будут рассмотрены ниже. Это — вибрации приемного устройства относительно рассматриваемой картины, вибрации индикатора относительно наблюдателя, погрешности положения точки изображения во времени при сканировании (в процессе записи) и на индикаторном устройстве (в процессе воспроизведения). Движение приемного устройства относительно рассматриваемой картины наблюдается, когда устройство недостаточно стабилизировано, чтобы скомпенсировать колебания платформы и ветровую нагрузку. Вибрации индикатора относительно наблюдателя происходят, когда скорости и амплитуды колебаний платформы столь велики, что перемещения тела и головы наблюдателя уже не могут быть скомпенсированы зрительным аппаратом. Погрешности при сканировании возникают, когда от кадра к кадру несколько меняется угол наклона сканирующего зеркала относительно его номинального значения. Ошибки воспроизведения возникают, когда положение линии сканирования на индикаторе неточно соответствует положению линии сканирования на входе.
Случайные перемещения с частотами, не превышающими ~2 Гц, не вызывают заметного размытия изображения, поскольку постоянная времени глаза слишком мала, чтобы воспринять эти перемещения слитно. В связи с тем что механизм, позволяющий глазу выделять информацию при наблюдении движущегося изображения объекта, в настоящее время недостаточно хорошо понят, невозможно определенным образом связать движение с ухудшением ОПФ. Однако чисто случайные перемещения и ошибки положения можно, по-видимому, описать фурье-преобразованием функции плотности вероятности положения изображения, когда эта функция непрерывна. Например, сигналы датчика положения сканирующей системы или ошибки синхронизации с гауссовым распределением плотности вероятности с центром, соответствующим правильному положению, должны иметь МПФ в форме гауссоиды с таким же среднеквадратичным отклонением сигма, что и у функции плотности вероятности.