Глава 6 Оптика
- Элементы оптических систем
Используя простейшую классификацию оптических систем, можно разделить их на линзовые, зеркальные и комбинированные зеркально-линзовые. Выбор оптической системы на основании предъявляемых к ней требований осложняется тем, что каждому типу систем присущи свои достоинства и недостатки.
При определенном диаметре и фокусном расстоянии потери на отражение и поглощение в линзовой системе будут больше, чем в зеркальной, однако суммарная эффективность зеркальной системы может оказаться выше или ниже эффективности линзовой системы в зависимости от степени экранирования зеркала в центре. Зеркальная (отражающая) оптическая система обычно легче по весу и дешевле, чем линзовая оптическая система тех же размеров, однако зеркальные системы могут и не обеспечить столь качественное изображение, как линзовые. Например, сферические зеркала нельзя исправить по внеосевым аберрациям, не применяя преломляющую коррекционную пластину, в то время как систему линз со сферическими поверхностями легче сбалансировать по аберрациям при расчете. Поскольку сферические поверхности изготовлять дешевле, чем асферические, это важное преимущество. С другой стороны, линзовые системы в отличие от зеркальных имеют хроматические аберрации. При проектировании систем FLIR существует тенденция отдавать предпочтение линзовым системам в связи с тем, что в этом случае существует много способов получить в компактных конструкциях изображение высокого качества. Однако преимущество отражательной оптики по стоимости заставляет вновь пересматривать обоснованность этой тенденции всякий раз, когда начинается разработка новой оптической системы.
Рассматривать оптическую систему независимо от системы сканирования трудно, поскольку обе системы тесно связаны: выбор второй в значительной мере влияет на разработку первой и наоборот. Таким образом, нужно кратко рассмотреть системы сканирования. Они разделяются на два типа в зависимости от

Фиг. 6.1. Сканирующие устройства в параллельном (а) и сходящемся (б) пучках.
того, осуществляется сканирование в сходящемся или параллельном пучке лучей.
В первом случае сканирующее устройство работает в той части оптической системы, где лучи сходятся, т. е. вблизи фокуса. В типичных схемах сканирующее устройство располагается между ближайшим к фокусу преломляющим элементом и линейкой чувствительных элементов приемника излучения. При работе сканирующего устройства в параллельном пучке оно располагается в той части оптической системы, где лучи параллельны или специально коллимируются. Если сканирующее устройство рас-
положено перед оптической системой, его иногда называют сканирующим устройством в пространстве объектов. Сканирующее устройство может быть также расположено между парой линз оборачивающей системы. Два примера приведены на фиг. 6.1.
Выбор того или другого вида сканирующей системы для конкретного применения производится по результатам сравнительного анализа. Для сканирующей системы в сходящемся пучке в общем случае требуется меньше элементов, однако она вносит аберрации и искажения в сходящийся пучок, которые необходимо корректировать.
Для системы сканирования в параллельном пучке в общем случае требуется более сложная и громоздкая оптика, но качество изображения не столь чувствительно к отклонениям зеркал от плоскостности, как в сходящемся пучке. Сканирующий элемент в параллельном пучке должен соответствовать максимальному размеру проекции входного зрачка, поскольку обычно требуется разместить сканирующее устройство в пределах оптической системы. Имея в виду эти различия, можно перейти теперь к рассмотрению оптических систем.
- Основные законы геометрической оптики
Рассмотрим в идеализированном виде два интересующих нас оптических явления: преломление на границе двух прозрачных диэлектрических сред, как в линзе, и отражение от поверхности идеального проводника, как в зеркале. Рассмотрим фиг. 6.2, на которой показана граница между двумя диэлектриками. Каждый материал характеризуется параметром, который называется показателем преломления п и представляет собой отношение скорости света в вакууме к скорости света в материале. Для немагнитных
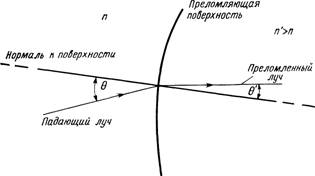
Фиг. 6.2. Преломление.
материалов величина п равна корню квадратному из диэлектрической постоянной, соответствующей данной оптической частоте. Показатели преломления оптических материалов, применяемых в тепловидении, приведены в разд. 6.8.
На фиг. 6.2 иллюстрируется закон преломления (закон Снеллиуса), согласно которому углы падения 0 и преломления 0', измеряемые от нормали к поверхности, связаны при переходе из среды с показателем п в среду с показателем п соотношением
sin 07sin 0 = п/п', (6.1)
или
![]()
(6.2)
Преломленный луч приближается к нормали, когда п* > п.
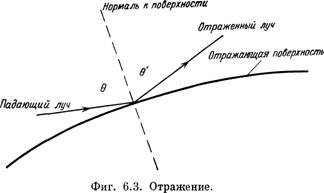
Отражение от идеального проводника (зеркала) иллюстрируется на фиг. 6.3. Согласно закону отражения,
![]()
(6.3)
- Оптический клин
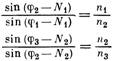
Полезным оптическим элементом является преломляющий клин (фиг. 6.4). Формулу, определяющую отклонение луча клином, можно вывести следующим образом. С учетом обозначений, приведенных на фиг. 6.4, используя закон преломления для первой и второй поверхностей, получаем
(6.4)
(6.5)

Фиг. 6.4. Преломление луча оптическим клином.
W — угол при вершине клина; ф4, ф2, ф3 — углы между падающим, преломленным и выходящим лучами соответственно и горизонталью; Ni, N2 — углы между нормалями к поверхности и горизонталью; nit п2, п3 — показатели преломления.
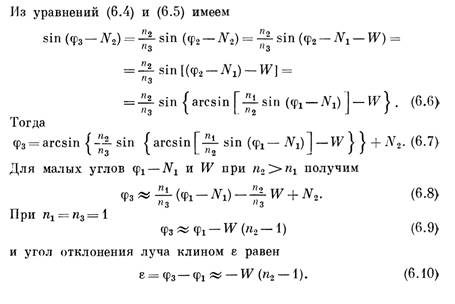

Ф1 | Фя | Фз (приблизительные значения) |
0° | —32,526° | -30,03° |
5 | —26,564 | -25,03 |
10 | -21,026 | -20,03 |
15 | — 15,840 | — 15,03 |
Таким образом, данное приближение является не очень точным даже для малых значений углов.
Клин является полезным оптическим элементом, поскольку при вращении клина вокруг какого-либо выходящего луча происходит сканирование падающего луча в пространстве объектов по кругу. Как показано в разд. 7.5, это свойство можно использовать в сканирующих системах.
- Простая линза
Простейшая преломляющая фокусирующая оптическая система состоит из одиночной линзы со сферическими поверхностями (фиг. 6.5). Простая линза характеризуется четырьмя параметрами: радиусами кривизны R1 и /?2, показателем преломления п и толщиной t. В соответствии с общепринятым правилом знаков радиус поверхности считается положительным, когда центр кривизны расположен справа от поверхности, и отрицательным, когда центр кривизны расположен слева от поверхности. R1— положительный радиус левой, a R2 — отрицательный радиус правой поверхности.
Простая линза называется тонкой, если толщиной t можно пренебречь. Представляют интерес три способа получения изображения с помощью простой линзы (фиг. 6.6). В первом случае параллельный пучок лучей от бесконечно удаленного точечного источника фокусируется за линзой на расстоянии / от нее. Отре-

Фиг. 6.5. Простая линза со сферическими поверхностями.

Фиг. 6.6. Способы получения изображения с помощью простой линзы.

Фиг. 6.7. Фокусирующее действие типичной линзы инфракрасной системы.
зок / называется фокусным расстоянием линзы. В первом приближении величина / определяет сдвиг s в изображении бесконечно удаленного объекта, лучи от которого попадают на линзу под небольшим углом а к оси (фиг. 6.7):
(6.11)
s = of.
Во втором случае точечный источник, находящийся на расстоянии / перед линзой, дает параллельный пучок лучей за линзой. В третьем случае точечный объект, находящийся на расстоянии О от линзы, отличающемся от бесконечности и от /, дает изображение в виде точки на расстоянии i от линзы, определяемом уравнением тонкой линзы
![]()
(6.12)

где
(6.13)
или
![]()
(6.14)
Эти соотношения выводятся в разд. 6.4.
Из приведенных уравнений видно, что важную роль играет величина показателя преломления материала, из которого сделана линза. Чем больше показатель преломления, тем больше могут быть радиусы для обеспечения данного фокусного расстояния. С увеличением радиусов облегчается изготовление линзы, появляется возможность получить более равномерное просветляющее покрытие на ее поверхности и уменьшить толщину линзы, что приводит к уменьшению потерь на поглощение излучения.
На фиг. 6.8 показаны все возможные типы простых линз. Линза называется положительной, или собирающей, если она фокусирует падающий на нее параллельный пучок лучей, и отрицательной, или рассеивающей, если она рассеивает падающий на нее параллельный пучок лучей. Заметим* что из восьми линз, изображенных на фиг. 6.8, две отличаются только тем, что они перевернуты, так что имеется только шесть типов простых линз. Фокусное расстояние толстой линзы толщиной t определяется формулой
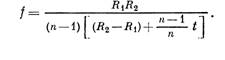
Можно показать, что увеличение фокусного расстояния Д/ линзы с увеличением ее толщины t описывается соотношением
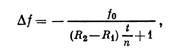 (6.16)
(6.16)
где /о — фокусное расстояние тонкой линзы с t = 0. Вывод уравнений для толстой линзы приводится в разд. 6.4.

