- Обнаружение объектов на фоне случайных шумов
Обнаружение простых объектов на фоне случайных шумов является хорошо изученным визуальным процессом. Исследовано маскирующее действие двух основных типов шумов. Это — не зависящие от сигнала аддитивные гауссовы шумы, типичные для фотонных приемников излучения, работающих при высоком уровне фона, и зависящие от сигнала мультипликативные пуассоновы шумы, присущие оптическим сигналам и типичные для приемников излучения, работающих при низком уровне фона. Попытки объяснить сущность обнаружения визуальной системой оптических сигналов на фоне шумов, распределенных по законам Гаусса и Пуассона, и теоретически предсказать результаты эксперимента делаются на основе флуктуационной теории. История развития и основные положения флуктуационной теории рассмотрены Jlero [53]. В последующих разделах данной главы рассмотрены отдельно два типа шумов, суммированы результаты экспериментов и показана их взаимосвязь.
- Обнаружение на фоне не зависящих от сигнала шумов
Вероятность обнаружения различных простых объектов на фоне аддитивных белых гауссовых шумов исследовалась Кольтманом [54], Кольтманом и Андерсоном [32], Шаде [38], а также Розеллом и Вильсоном [39]. Кольтман и Андерсон получали прямоугольную волну на телевизионном экране на фоне белого гауссова шума и определяли порог обнаружения в зависимости от пространственной частоты. Шаде определял условия обнаружения на фотографиях трехштрихового тест-объекта на фоне шумов. Розелл и Вильсон определяли пороги обнаружения прямоугольных тест-объектов на фоне «живых» шумов на телевизионном экране. Некоторые из этих экспериментальных результатов представлены на фиг. 4.20 для конкретных значений постоянной времени глаза Те, частоты обновления информации F, площади объекта на индикаторе At, площади корреляции шумов на индикаторе Ас (номинально соответствующей элементу разрешения), спектра напряжения шума g (/) и МПФ видеоконтрольного устройства гш. Все эти эксперименты убедительно показывают, что вероятность
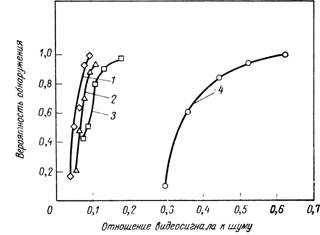
Фиг. 4.20. Вероятность обнаружения в зависимости от отношения видеосигнала к шуму для прямоугольных тест-объектов [39].
Размеры тест-объектов: 1 — 4 х 180 строк; 2 — 4 х 128 строк; з—4 х 64 строк; 4 — 4x4 строк.
обнаружения является однозначной функцией отношения сигнала к шуму, если остальные параметры качества изображения остаются постоянными.
Кольтман с Андерсоном, Шаде, а также Розелл с Вильсоном обобщили эти результаты на широкий класс условий, используя концепции о пространственных и временных интегрирующих свойствах системы. Эффект пространственного интегрирования учитывается предположением, что глаз улучшает отношение сигнала к шуму изображения в (AtlAc)1/*раз, а улучшение за счет временного интегрирования учитывается коэффициентом (TeF)1!2. Тогда можно определить воспринимаемое отношение сигнала к шуму (С/Щ)р1) формулой
(4.14)
где (С/Ш)i — отношение сигнала к шуму в точке изображения, т. е. в области корреляции Ас, а
(4.15)
Экспериментальные данные такого рода описываются универсальной кривой, показанной на фиг. 4.21 и устанавливающей связь между вероятностью обнаружения и (С/Ш)р. Нормализованные данные с фиг. 4.20 показаны в виде точек, наложенных на теоретическую кривую фиг. 4.21.
*Розелл относит эту величину к индикатору (С/Ш). Мы считаем такое обозначение неточным, поскольку речь идет об отношении сигнала к шуму, воспринимаемому визуальной системой.
Эта кривая представляет интегральный закон распределения гауссовой плотности вероятности. Обозначая вероятность обнаружения как функцию (С/Ш)р через Р(с/ш)р, имеем
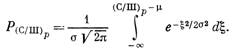(4.16)
Данные Розелла и Вильсона [39] дают среднеквадратичное отклонение а порядка 1 и среднюю величину \х порядка 3,2. Уравнение (4.16) можно сформулировать следующим образом. Величина Р(с/т) есть вероятность того, что сигнал плюс мгновенное значение шума превышают 3,2а. Другой смысл этой функции распределения вероятности заключается в том, что вероятность правильного обнаружения сигнала на экране индикатора равна вероятности того, что отношение сигнала к шуму равно 3,2 или больше.
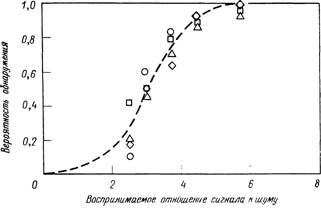
Фиг. 4.21. Вероятность обнаружения прямоугольных тест-объектов в зависимости от (С/Ш)р [39].
Размеры тест-объектов: О 4 X 180 строк; д 4х 128 строк; □ 4 х 64 строк;0 4x4 строк.
Различные эквивалентные выражения для этой функции имеют вид
Для (С/Ш)р > 1 эта функция может быть аппроксимирована более простым выражением
(4.17)
(4.18)
(4.19)
(4.20)
(4.21)
где пары параметров А и В могут иметь различные значения. Проще всего принять А = 1, В = 0,15. Использование при анализе приближенной формулы (4.21), по-видимому, внесет небольшую погрешность по сравнению с точной формулой.
При этом принимается гипотеза, что визуальная система устанавливает порог отношения сигнала к шуму как средство оценки
значимости нервных импульсов. В результате при низком отношении сигнала к шуму оптические сигналы не обнаруживаются, однако и шумы очень низкого уровня не принимаются за сигналы. Таким образом, мы не воспринимаем периодически возникающие несуществующие объекты (ложные тревоги).
Необходимо отметить, что данные Розелла и Вильсона [39] дают среднюю характеристику для различных наблюдателей. Интервал изменения отношения сигнала к шуму от условий обнаружения с малой вероятностью к условиям обнаружения с высокой вероятностью для отдельных наблюдателей может быть уже, чем это следует из фиг. 4.21, и полученное гауссово распределение является следствием различий в индивидуальных порогах и изменений условий наблюдения во времени. Читатели, имеющие дело с тепловизионными системами, могут экспериментально определить собственный порог, используя регулируемый тепловой источник для получения различных значений отношения сигнала к шуму.
- Обнаружение на фоне зависящих от сигнала шумов
Источник света, испускающий N фотонов в секунду, характеризуется пуассоновым распределением эмиссии фотонов со средним значением N и среднеквадратичным отклонением УN. Поэтому любой оптический сигнал не свободен от шумов; шумы всегда присутствуют как следствие случайного характера эмиссии фотонов. Отношение средней величины сигнала к среднеквадратичной величине шума равно N/УN = У N; такой фотонный шум называется зависящим от сигнала. Любая оптическая система обнаружения, в том числе и глаз, в конечном счете ограничивается шумами оптических сигналов [41, 55, 56].
Блэкуэлл [44, 57—59] опубликовал результаты многочисленных экспериментов, в которых он определял способность глаза выделять простые сигналы на равномерном фоне в условиях, когда источники не имели других шумов, кроме фотонных. Эти классические эксперименты позволили определить предельные способности глаза обнаруживать простые объекты на равномерных фонах. Объекты представляли собой круглые диски различных размеров и яркости, фоном служили большие (от 10 до 60°), равномерно освещенные поля переменной яркости. В ходе экспериментов изменялись яркость фона (поля адаптации) LB, продолжительность предъявления объекта t и угловой диаметр объекта 0. Для группы наблюдателей определялась 50%-ная вероятность обнаружения объекта за время наблюдения. Все данные выражены в величинах порогового контраста С = (LT — LB)/LB.
В первой серии экспериментов 1946 г. наблюдателям предлагалось определить, в каком из восьми возможных положений на-
ходится объект, предъявляемый в известный наблюдателю момент времени. Яркость фона изменялась от 3*10“6 до 4-102 кд/м2, угловые размеры объектов — от 1,05 до 35,1 мрад, продолжительность предъявления составляла 6 с. Результаты представлены графически на фиг. 4.22. Аналогичные результаты были получены для отрицательных контрастов. Во второй серии экспериментов 1946 г. наблюдателю были известны положение объекта и момент его предъявления, а продолжительность предъявления t выбиралась достаточной для максимально возможной временной суммации, но не превосходила 15 с. Угловые размеры объектов изменялись от 0,173 до 105 мрад, а яркость — от 3 -10~6 до 2,5 -102 кд/м2. Результаты представлены на фиг. 4.23.
В экспериментах, проводившихся в период с 1950 по 1952 г., наблюдателям предлагалось выбрать интервал времени предъявления объекта с известным положением и размером из четырех известных интервалов. Яркость изменялась от 0 до 300 кд/м2, размеры объекта — от 0,233 до 14,9 мрад, продолжительность предъявления — от 10~3 до 1 с. В экспериментах 1956—1957 гг. диапазон изменения яркости фона составлял 0,3—1000 кд/м2, диапазон размеров объекта 0,29—16,98 мрад, а время предъявления составляло 1, 0,1 и 0,01 с. Результаты этих экспериментов аналогичны данным 1946 г. Интересно представить данные 1950—1952 гг. в координатах, использованных для построения фиг. 4.24 и 4.25. На фиг. 4.24 зависимость порогового контраста от углового размера объекта при постоянной яркости фона ясно показывает, что механизм пространственной суммации действует до угловых размеров ~10 мрад. Из фиг. 4.25 следует, что временное суммирование также оказывает существенное влияние до интервалов времени 0,5 с.
Из опытов 1946 г. Блэкуэлл сделал важный вывод, что вероятность обнаружения в функции контраста имеет форму нормальной кривой, описываемой уравнением
(4.22)
где среднеквадратичное отклонение о равно 0,5, а Си0р — измеренный пороговый контраст.
Таким образом, обнаружение сигналов на фоне зависящих от сигнала шумов описывается как случайный гауссов*процесс, механизм которого сходен с механизмом, наблюдаемым в случае аддитивных шумов. Блэкуэлл предположил, что среднее воздействие на нервную систему, или возбуждение Е стимулом L, есть линейная функция L.
Фиг. 4.23. Пороговый контраст в зависимости от яркости фона и размера объекта [57].
Продолжительность предъявления до 15 с; размеры объекта, мрад: 1 — 0,173; 2 — 1,05; — 2,81; 4 — 5,29; 5 — 16,1; 6 — 35,1.
Фиг. 4.24. Пороговый контраст в зависимости от размера объекта и яркости фона [44].
Продолжительность предъявления, с
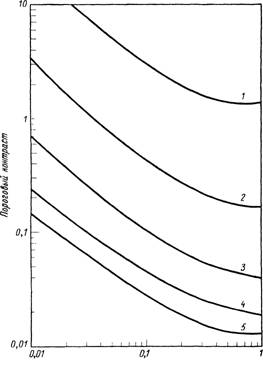
Фиг. 4.25. Пороговый контраст в зависимости от продолжительности предъявления и яркости фона [44].
Размер объекта 1,16 мрад; яркость фона, кд/л?2; j — 0,03; 2 — 0,3; 3 — з; 4 — 30; 5 — 300.
Продолжительность предъявления 1 с; яркость фона, кд/м2;
- —0,03; 2 — 0,3; з — З; 4—30; 5—300.
Фиг. 4.22. Пороговый контраст в зависимости от яркости фона и размера объекта [57].
Продолжительность предъявления 6 с; размеры объекта, мрад: 1 — 1,05; 2 — 2,81; 3 — 5,29; 4 — 16,1; 5 — 35,1.
/ в,пд/м2
При решении задачи обнаружения AL на фоне L в по предположению Блэкуэлла визуальная система оценивает разброс Е относительно среднего значения Ев, соответствующего яркости фона L в, и устанавливает критерий сравнения Ес, пропорциональный Ев. Критерий Ес используется затем для оценки, насколько существенны отклонения мгновенных значений Е от Ев. Предполагается, что каждое возбуждение Е == = Е в -г АЕ сравнивается с Еси время (в процентах от общего времени наблюдения), в течение которого Е превышает Ес, определяет вероятность принятия решения о присутствии сигнала AL, соответствующего АЕ. Другими словами, величина ДЕ должна превысить Ес — Ев, чтобы вероятность обнаружения превысила 50%. Такой же механизм предлагался Шаде [38], а также Розеллом и Вильсоном [391 для объяснения своих экспериментов.
В более поздней статье [59] Блэкуэлл указал, что кривые порога AL в функции L в, углового размера объекта и продолжительности предъявления достаточно точно описываются уравнениями вида
(4.23)
где аг и а2 — сложные функции продолжительности предъявления и размера объекта.
Рассмотрим теперь выводы Ори [601, относящиеся к проблеме визуального обнаружения объектов. Выше было указано, как эксперименты Шаде, Розелла и Вильсона, а также Блэкуэлла подтверждают гипотезу, что визуальная система обнаруживает наличие или отсутствие оптического сигнала на фоне гауссовых шумов на основе принципов теории статистических решений. Ори выдвинул гипотезу, что вероятность обнаружения Р (т. е. принятия правильного решения о присутствии или отсутствии сигнала) определяется в пространстве нервных возбуждений, так что
(4.24)
где Е — нервные возбуждения. Величины Е или £ представляют собой переменные интегрирования; Ет — мгновенное значение общего числа нервных возбуждений, состоящих из Ев возбуждений, соответствующих фону, и АЕ возбуждений, соответствующих сигналу; Ет =Ев-\-АЕ. Среднеквадратичное отклонение изменений (шума) относительно Ет равно от. Величина Р, определяемая уравнением (4.24), есть вероятность того, что мгновенное значение общего числа нервных возбуждений Ет превосходит пороговую величину К. Смысл величины К в том, что глаз устанавливает порог, при превышении которого возбуждение имеет природу сигнала. Это прямое развитие гипотезы Шаде и Блэкуэлла с тем отличием, что Ори постулирует сложную зависимость порогового критерия от уровня освещенности, что позволяет глазу работать в диапазоне изменения яркости на шесть порядков. Используется
нормальный (гауссов) закон распределения шумов, поскольку считается, что на всех уровнях яркости фотонный поток достаточно велик, чтобы можно было аппроксимировать распределение Пуассона распределением Гаусса. Таким образом, как фотонный шум, связанный с дискретной природой света, так и электронные шумы системы могут рассматриваться как процессы, подчиняющиеся нормальному (гауссову) закону. В случае чисто фотонных шумов
(4.25)
Ори предположил, что пороговая величина К описывается выражением вида К = ЕВАГС, где С зависит от шума и может быть выражена формулой
(4.26)
При такой записи верхний предел второго интеграла в уравнении (4.24) равен
(4.27)
Первый член в правой части формулы (4.26) определяет абсолютный нижний предел обнаружения сигнала; второй — порог обнаружения компоненты сигнала, пропорциональной шумам, так что обнаружение зависит от определенного уровня отношения сигнала к шуму; третий — зависимость порога от контраста. Таким образом, модель Ори объясняет три известных из литературы случая зависимости обнаружения сигнала от уровня яркости:
- Абсолютный порог обнаружения.
- Зависимость обнаружения от отношения сигнала к шуму при средних уровнях яркости.
- Ограниченное значением контраста обнаружение при высоких уровнях яркости.
Анализ исследований и данных Блэкуэлла проводился также Бейли [61], Оврингтоном и Лейвином [62], Корнфельдом и Лоусоном [63]. В этих работах приведены формулы, согласующиеся с данными Блэкуэлла и связывающие пороговую яркость объекта, его угловой размер, время наблюдения и яркость фона.
Испытания Блэкуэлла [571 проводились в идеальных лабораторных условиях, и поэтому полученные результаты нельзя непосредственно применять к практическим задачам обнаружения объектов, ограниченных значением контраста. Блэкуэлл привел рекомендации для практического использования в более поздней работе [44]. Де Вое и др. [641 провели эксперименты, аналогичные опытам Блэкуэлла, но в условиях, более близких к реальным. Они указали верхний и нижний пределы порогов (вместо одного
(50%) у Блэкуэлла), требуемые для решения различных практических задач.
Основы флуктуационной теории были в первом приближении изложены Роузом [56]. По его наблюдениям квантовые флуктуации шумов становятся практически незаметными при яркости порядка 3-10"2 кд/м2. При этой и более высокой яркости белая поверхность кажется ровной и свободной от шумов. Роуз указал, что статистические флуктуации играют важную роль в диапазоне яркостей от 3 -10"6 до 3 -10"2 кд/м2, а при яркости более 3 -102 кд/м2 в области, ограниченной значением контраста, роль флуктуаций сравнительно невелика.
