Глава 3 Теория линейной фильтрации
- Области применения
В практике тепловидения часто требуется описать реакцию системы на различные сигналы, оценить пространственное разрешение, разработать схемы для повышения качества изображения. Математический аппарат, применяемый для этих целей,— теория линейной фильтрации [1, 2], являющаяся ветвью фурье-анализа, используемого для изучения реакции на сигнал линейных инвариантных устойчивых систем. Теорию линейной фильтрации можно применять к оптическим, оптико-электронным, механическим и электронным приборам. Разработанная первоначально для описания электрических цепей и следящих систем, эта теория была распространена затем на оптические системы. Теория линейной фильтрации является частью теории анализа изображения и необходима при разработке и оценке любой тепловизионной системы.
Определяя систему, Гудмен [1] считает основным ее признаком способность преобразовывать ряд входных функций в ряд выходных функций. Будем рассматривать здесь только системы однозначных функций или взаимно однозначных преобразований, т. е. системы с шумами исключаются из рассмотрения. На фиг. 3.1 показана система координат и применяемые обозначения. Точка в пространстве объектов определяется угловыми координатами (#си У о), отсчитываемыми от оптической оси. Координаты (xiy yt) в плоскости изображения для системы без искажений определяются соотношениями xt = Мх0 и г/г = Му0, где М — угловое увеличение.
Теория линейной фильтрации применима только к таким оптическим системам, которые преобразуют распределение яркости объекта в распределение яркости изображения в результате свертки. В большинстве изображающих систем в максимально возможной степени осуществляются процессы свертки, так как именно эти процессы обеспечивают изображение наилучшего качества. Следовательно, понимание сущности процессов свертки является весьма важным; нужно также уметь отличать процессы, не подчиняющиеся закономерностям свертки.
Фиг. 3.1. Пространственные координаты в плоскости объекта и изображения.
3.2. Интеграл свертки
Рассмотрим двумерный объект, энергетическая яркость которого описывается распределением О (х0, у0) в координатах (х0, у0) в пространстве объектов. Действие изображающей системы на объект обозначим оператором S. Тогда распределение яркости в пространстве изображения
будет S {О (.х0, г/0)} «
Следствием линейности системы является возможность представления функции распределения яркости объекта в виде ряда более простых функций или в пределе в виде интеграла. Чтобы быть уверенным, что это важное упрощение возможно, ограничим рассмотрение системами, которые являются или могут быть аппроксимированы. линейными операторами во времени и пространстве, воздействующими на представляющие интерес сигналы.
В общем случае функции распределения яркости объекта являются четырехмерными функциями пространства и времени, однако при анализе обычно считают, что глубина не имеет значения, и описывают объекты функциями двух угловых пространственных координат и одной временной координаты. Функцию распределения яркости объекта удобно разложить на комбинацию взвешенных дельта-функций Дирака, используя так называемое фильтрующее свойство дельта-функции б (х). Математически это записывается в двух измерениях в виде
(3.2)
а геометрическая интерпретация дана на фиг. 3.2. Смысл рассматриваемого интеграла заключается в том, что любую функцию можно представить как бесконечную сумму взвешенных и смещенных дельта-функций.
Распределение яркости изображения I (xh yt) определяется следующим образом:
(3.3)
Предполагая, что выполняется свойство линейности, получаем
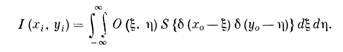(3.4)
Таким образом, функция распределения яркости изображения представляет собой взвешенную сумму реакций системы на дельтафункции, являющиеся компонентами объекта.
Функция
называется функцией рас
сеяния точки или импульсной реакцией системы. Соотношение (3.4) называется интегралом суперпозиции, так как функция I (xt, yt) выражается как интеграл от наложенных друг на друга реакций на дельта-функцию, соответствующих бесконечно малым пространственным интервалам. В теории электромагнитного поля количественным аналогом функции рассеяния точки является функция Грина для точечного заряда или источника тока, а в теории электрических цепей — реакция на импульс тока или напряжения.
Фиг. 3.2. Фильтрующее свойство дельта-функции.
а _ распределение яркости объекта; б'—дельта-функция; в — интеграл от произведения распределения яркости объекта на дельта-функцию.
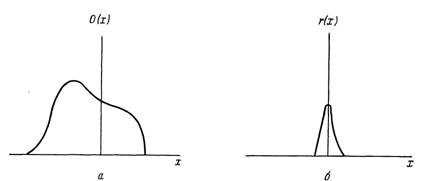
Фиг. 3.3. Распределение яркости объекта (а) и функция рассеяния (б).
Обобщим записанный результат на трехмерный случай, полагая, что временная задержка реакции на входной сигнал пренебрежимо мала:
Интеграл суперпозиции упрощается в случае пространственной инвариантности системы, т. е. если импульсная реакция системы не зависит от времени и положения импульса 1). Полагая для простоты увеличение М равным единице, получим
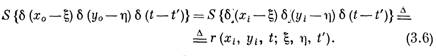
Приведенный ниже графический пример показывает, что интеграл суперпозиции приобретает упрощенную форму, называемую интегралом свертки, в случае, когда система пространственно инвариантна, т. е. когда форма импульсной реакции г не меняется при смещении относительно осей координат. Рассмотрим распределение яркости объекта и функцию рассеяния, показанные на фиг. 3.3. Распределение яркости изображения можно найти, разлагая распределение яркости объекта на взвешенные дельта-функции, заменяя каждую из этих дельта-функций функцией рассеяния и производя суммирование, как показано на фиг. 3.4.
В действительности системы тепловидения с кадровой разверткой не инвариантны во времени, поскольку данная точка объекта создает сигнал только в течение малого промежутка общего времени. Однако мы рассматриваем действие системы при наблюдении интегрирующим во времени прибором, таким как зрительный аппарат человека. Следовательно, когда объект неподвижен относительно системы можно считать, что система инвариантна во времени.
а 6 б
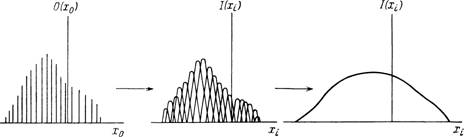
Фиг. 3.4. Построение функции распределения яркости изображения путем разложения функции распределения яркости объекта (а), замены дельтафункций взвешенными функциями рассеяния (б) и суммирования (в).
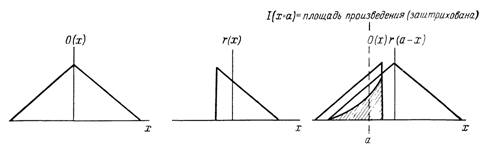
Фиг. 3.5. Свертка.
3.3. Преобразование Фурье
В одномерном случае прямое преобразование Фурье определяется формулой
(3.11)
Пространственная частота /х (пространство описывается декартовыми координатами) является аналогом обычной временной или электрической, частоты /*. Частота ft измеряется в герцах, а пространственная частота fx — в единицах мрад"1. Смысл пространственной частоты ясен из фиг. 3.6, на которой показано синусоидальное изменение интенсивности источника света с пространственным угловым периодом 0Х. Источник рассматривается с достаточно большого расстояния /?, чтобы можно было приближенно считать
(3.12)
На фиг. 3.7 показана связь пространственных частот в плоскостях объекта и изображения с угловым увеличением для случая наблюдения изображения на экране. Периоды тест-объекта и его изображения равны соответственно 2a0/R0 и 2а пространственные частоты составляют R0i2a0 и Ril2at. Угловое увеличение М равно
(3.13)
В трех измерениях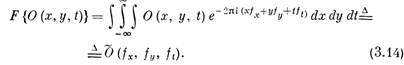 
Фиг. з.б. Пространственная частота.
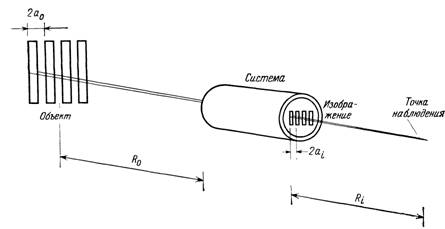
Фиг. 3.7. Угловое увеличение.
Обратное преобразование имеет вид г)
(3.15)
для одномерного случая и
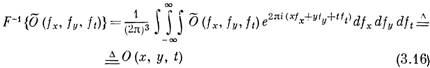
для трехмерного случая.
Последовательно проведенные прямое и обратное преобразования дают исходную функцию, т. е.
Подробное рассмотрение преобразования Фурье и его приложений дано, например, в книге Брейсуэлла [3] *),
*На русском языке см., например, Снеддон И., Преобразование Фурье. ИЛ, 1955.— Прим. перев.
3.4. Теорема свертки и оптическая передаточная функция
Когда система осуществляет ряд последовательных сверток и приходится иметь дело со сложным объектом и различными функциями рассеяния, процесс трудно проанализировать и представить себе наглядно. Теорема свертки в фурье-анализе позволяет перейти в область частот, где эти операции производить намного легче. Теорема гласит, что преобразование Фурье свертки двух функций равно произведению преобразований этих функций. Применительно к уравнению (3.10), описывающему изображение, эта теорема записывается в виде.,
(3.17)
Соответствующее сокращенное обозначение имеет вид
(3.18)
Преобразование Фурье г импульсной реакции г называется оптической передаточной функцией (ОПФ). Если каждая компонента системы линейна и не зависит от других компонент, то реакция системы в целом rs есть результат ряда сверток
(3.19)
Тогда в соответствии с теоремой свертки для получения ОПФ системы нужно перемножить последовательные передаточные функции
(3.20)
и спектр изображения оказывается равным
(3.21)
Таким образом, сложную операцию многократных сверток можно заменить более простой операцией нахождения обратного преобразования произведения преобразований свертываемых функций. Это позволяет также представить процесс получения изображения как селективное взвешивание системой спектра пространственных частот объекта в частотной области (фиг. 3.8). Таким образом, ОПФ есть мера способности изображающей системы воспроизводить пространственные частоты, содержащиеся в картине.
ОПФ — комплексная функция, модуль, или абсолютная величина, которой является модуляционной передаточной функцией (МПФ) *). МПФ представляет собой амплитуду реакции системы на синусоидальную волну. Значение этой функции условно принято за единицу при нулевой частоте или близкой к ней.
г) В отечественной литературе модуляционная передаточная функция (МПФ) обычно называется частотно-контрастной характеристикой (ЧКХ), а в переводах — функцией передачи модуляции (ФПМ). В данном случае используется название модуляционная передаточная функция (МПФ) по аналогии с оптической передаточной функцией (ОПФ).— Прим. перев.
Фиг. 3.8. Ослабление частот объекта модуляционной передаточной функцией (МПФ) в зависимости от пространственной частоты /.
Аргумент оптической передаточной функции в радианах называется фазовой передаточной функцией (ФПФ) и определяет фазовый сдвиг пространственной частоты, вносимый системой. Комплексное выражение ОПФ имеет вид
(3.22)
Многие из теоретических положений, относящихся к ОПФ и содержащихся в литературе по оптическим и телевизионным системам, применимы и к системам тепловидения, если выполняются следующие условия: 1) излучение воспринимается некогерентно; 2) обработка сигнала линейна; 3) воспроизведение изображения — пространственно инвариантный процесс; 4) преобразование, осуществляемое системой, однозначно (в частности, происходит без шумов). Последние три условия в тепловизорах обычно нарушаются. В инфракрасной оптической системе не выполняется условие пространственной инвариантности, если импульсная реакция меняется от центра к краю поля зрения из-за аберраций и если сканирование нелинейно во времени, в результате чего электрические фильтры будут иметь различные значения ОПФ на одной и той же частоте в различных участках поля зрения. Линейка чувствительных элементов приемника излучения осуществляет периодическую выборку в направлении, перпендикулярном направлению сканирования, поэтому преобразование изображения не подчиняется закономерностям свертки. Каждый приемник имеет шумы, из-за чего нарушается условие однозначности преобразования. Аналоговые электронные схемы вносят как шумы, так и нелинейность. Нелинейное сжатие можно специально использовать в канале обработки видеосигнала для улучшения динамического диапазона системы. Преобразование электрического сигнала оптическим индикатором также может быть нелинейным.
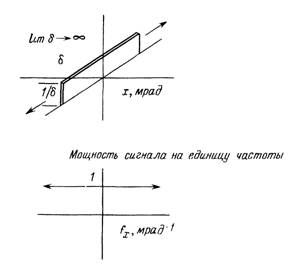
Фиг. 3.9. Линейный источник и его спектр.
Кроме того, системы тепловидения могут отличаться от других оптических и оптико-электронных приборов по следующим четырем причинам. Во-первых (и это наиболее важно), в тепловизоре уровень, соответствующий средней яркости картины, обычно вычитается из видеосигнала и на экране индикатора отображаются только изменения яркости относительно среднего уровня, к которым добавляется по желанию любой постоянный сигнал. Во-вторых, производя формирование сигнала с помощью электронной системы или используя специальные индикаторные устройства, можно получить функции рассеяния с отрицательными амплитудами и МПФ с амплитудой, большей единицы, что вносит определенную специфику при оценке ОПФ. В-третьих, различные рабочие точки квазилинейной системы могут иметь разные ОПФ. В- четвертых, изображение может образовываться в результате процесса выборки, не обеспечивающего достаточной фильтрации, так что ОПФ проявляет себя только в направлении, перпендикулярном направлению выборки.
Поэтому, когда мы говорим об ОПФ тепловизионного прибора, то вводим, по существу, довольно ненадежную систему оценки. Тем не менее целесообразно принять эту систему как средство конструирования, анализа и описания тепловизионных приборов, так как ОПФ является удобным мерилом качества изображающей системы. В связи с этим при анализе, описании и эксперимента льном определении ОПФ требуется максимум предосторожностей, чтобы убедиться, что все указанные выше отклонения от необходимых для существования ОПФ условий устранены или учтены.
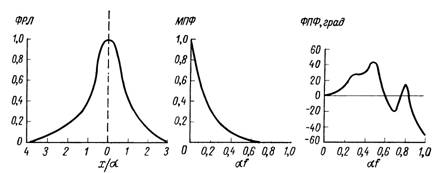
Фиг. 3.10. Функция рассеяния линии (ФРЛ), модуляционная передаточная функция (МПФ) и фазовая передаточная функция (ФПФ).
Поскольку во многих системах тепловидения не выполняются условия существования ОПФ во всех направлениях, часто необходимо иметь функцию рассеяния в направлении, где условия выполняются. Это приводит к определению функции рассеяния линии (ФРЛ), которая представляет собой реакцию на источник в виде длинной, бесконечно тонкой линии, составленной из ряда следующих друг за другом дельта-функций. Такой линейный источник содержит пространственные частоты только в направлении, перпендикулярном длине линии, причем присутствуют все пространственные частоты от нуля до бесконечности с амплитудами, равными единице (фиг. 3.9). Поэтому преобразование Фурье от функции рассеяния линии одномерно.
Так как сигнал, соответствующий этой линии, проходит через каждую компоненту системы, частотный состав сигнала селективно ослабляется. Изображение на выходе не соответствует точно сигналу на входе, наблюдается размытие изображения линии. Пример ФРЛ, МПФ и ФПФ для системы тепловидения в направлении сканирования приведен на фиг. 3.10. Заметим, что асимметрия ФРЛ указывает на наличие фазового сдвига. В системах тепловидения основной вклад в ФРЛ и МПФ обычно дает конечный угловой размер приемника излучения а, поэтому координату х можно выразить в единицах а, а частоту — в единицах 1/а.
Теория фурье-анализа была введена в оптику независимо Дюфье [4] в 1946 г., Шаде [5] в 1948 г. и Сельвином [6] в 1948 г. Общие вопросы фурье-оптики рассмотрены в книгах Гудмена [1], О’Нейла [2], Франсона [7] и Линфута [8]. Основные проблемы оптики рассматриваются в работах [9—17]; в качестве руководства по ОПФ оптических и оптико-электронных систем можно рекомендовать ряд отличных работ [20—33].
Фурье-анализ в оптике, за немногими исключениями, аналогичен анализу Лапласа в теории электрических цепей. Как указал О’Нейл [2], временные фильтры имеют два существенных отличия от пространственных. Во-первых, временные фильтры являются односторонними во времени и должны удовлетворять требованию физической осуществимости, т. е. изменения на выходе временного фильтра не могут проявиться раньше, чем они возникли на входе. Оптические же фильтры являются двусторонними в пространстве. Как показано во многих книгах по математике и теории электрической фильтрации, вследствие этой разницы становится целесообразным использовать при анализе временных фильтров одностороннее преобразование Лапласа, а не преобразование Фурье. Во-вторых, электрические сигналы могут быть положительными и отрицательными, в то время как интенсивность оптического сигнала всегда положительна.
3.2 Применение операции свертки к процессам воспроизведения изображения
Поскольку теория линейной фильтрации является широко используемым средством анализа изображения, часто имеет смысл аппроксимировать процессы, не подчиняющиеся закономерностям свертки (несвертываемые процессы) процессами, подчиняющимися закономерностям свертки (свертываемые процессы), так чтобы отклонения от истинного поведения были незначительными. Например, процесс получения изображения, характеризующийся умеренной пространственной неинвариантностью, может быть аппроксимирован свертываемым процессом по малым участкам поверхности объекта, называемым изопланатическими зонами. Изображение, образованное выборками свертки, большей частью будет достаточно хорошо отфильтровано, что делает процесс выборки близким к свертываемому. Аналогично влиянием небольших шумов и нелинейности обычно можно пренебречь.
Один из наиболее важных свертываемых процессов при получении теплового изображения — разложение изображения путем сканирования приемником излучения. Рассмотрим фиг. 3.11, где квадратный приемник с размерами а X а сканирует плоскость изображения (х, у), причем середина линии сканирования соответствует у = у'. Если приемник имеет равномерную по поверхности чувствительность и мгновенно интегрирует все падающее излучение, обеспечивая получение единого электрического сигнала, то при сканировании сигнал в точке х , у' определяется величиной I (х\ у') и зависит от распределения энергии в плоскости изображении
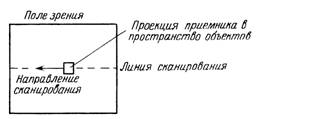
Фиг. 3.11. Сканирующий приемник излучения, женин О (х, у) следующим образом:
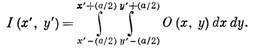(3.23)
Определим теперь импульсную реакцию приемника г (х) как
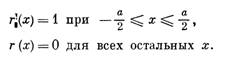(3.24)
При сканировании х принимает непрерывный ряд значений х', а у все время остается равным у'. Соответственно можно переписать уравнение (3.23) в виде
(3.25)
Интеграл в скобках представляет собой свертку; таким образом, процесс является свертываемым в направлении сканирования. Интеграл по у указывает на пространственную неинвариантность, так что в направлении, перпендикулярном сканированию, процесс является несвертываемым. Хорошо знакомый пример такого типа сканирования для получения изображения — телевизионное вещание. Можно привести множество других примеров несвертываемых процессов получения изображения. Строго говоря, к ним cледует отнести и зрение, поскольку используется конечное число приемников и разрешение падает от центра к краю поля зрения. Полутоновая газетная фотография — также несвертываемый процесс, поскольку в каждой точке он по интенсивности бинарный. Следовательно, это процесс одновременно нелинейный и не обладающий пространственной инвариантностью. Обычная фотография является нелинейным процессом, кроме того при проявлении наблюдаются эффекты соседства, что приводит к нарушению пространственной инвариантности. Однако такие
процессы могут рассматриваться и как свертываемые, если выбран соответствующий масштаб или анализируются только ограниченные площади.
