Силовые кабели - Сопротивление изоляции кабеля

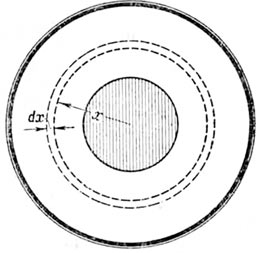
Фиг. 42. Схема одножильного кабеля.

До введения в практику оценки качества кабеля путем измерения потерь в диэлектрике сопротивление изоляции было главнейшим фактором суждения о качестве кабеля, причем некоторое время считалось, что, чем выше сопротивление изоляции, тем кабель лучше. Для силовых кабелей такое воззрение в настоящее время почти повсеместно оставлено, причем некоторые национальные стандарты, прежде всего нормы Союза германских электротехников, исключают всякое упоминание об этой величине, но вводят для кабелей высокого напряжения взамен этого испытание на потери в диэлектрике. Известный немецкий авторитет по кабельным вопросам R. Apt (40], сравнивая французские нормы с немецкими, отмечает как недостаток разработки французских норм то обстоятельство, что в них сохранено измерение сопротивления изоляции. Главнейшей причиной того, что величина сопротивления изоляции перестала играть прежнюю роль при оценке ячества изоляции кабеля, является то, что эта величина не стоит ни в какой взаимной связи с наиболее существенным свойством кабеля, а именно его электрической прочностью, и не характеризует срока службы кабеля.
Кроме того, сопротивление изоляции является чрезвычайно изменчивой величиной, зависящей от целого ряда факторов, часто трудно поддающихся учету. Сопротивление изоляции зависит от:

1. геометрических размеров кабеля;
2. состава пропиточной массы и, в частности, от содержания канифоли;
3. степени сушки и пропитки кабеля, причем, чем хуже высушен кабель, тем меньше сопротивление изоляции, и чем хуже пропитан кабель, тем больше сопротивление изоляции;
4. температуры изоляции;
5. высоты измерительного напряжения;

f) электрического состояния кабеля, т. е. от того, остался ли в диэлектрике заряд от предыдущего испытания напряжением или нет.
Часть этих факторов очень трудно поддается определению, в особенности температура кабеля, от которой чрезвычайно сильно зависит сопротивление изоляции.
Если обозначим через dw сопротивление изоляции элементарного кольцевого слоя одножильного кабеля (фиг. 42) на расстоянии х от центра кабеля, то можно написать
(190)
где р — удельное сопротивление изоляции.
Интегрируя уравнение (190), получим
где г — радиус проводящей жилы кабеля,

Зависимость между температурой и сопротивлением изоляции по М. Hоchstadter’y [45] была дана на фиг. 7, где кривая 1 изображает такую зависимость, а прямая 2— зависимость между law и температурой. В части кривой 1 от 35 до 60° С находится область перехода пропиточной массы из густожидкого в жидкое состояние.
Таблица 9
Зависимость между сопротивлением изоляции и температурой по L. Lichtenstein'y

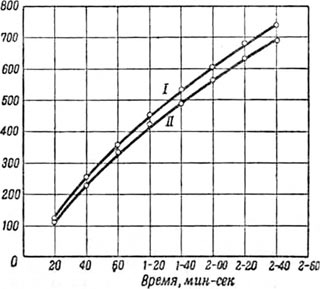
Фиг. 43. Влияние времени и направления тока на величину сопротивления изоляции.
Значительное влияние на величину сопротивления изоляции оказывает время выдержки диэлектрика кабеля под напряжением прямого тока.
Благодаря поглощению (абсорбции) электрического заряда диэлектриком кабеля и созданию в нем э.             д. с. обратного знака сопротивление изоляции сильно увеличивается с течением времени. Если через диэлектрик, подвергавшийся электризации прямым током, пропустить ток в обратном направлении, то сопротивление изоляции будет меньше первоначальною.
На фиг. 43 приведены две таких кривых сопротивления изоляции, снятых для кабеля на I 000V рабочего напряжения, 2 X 150 мм2, причем кривая 1 относится к измерению током, пропускаемым в одном направлении, а кривая II— в обратном направлении. Эти же обе кривые показывают, как быстро растет сопротивление изоляции с увеличением времени выдержки диэлектрика кабеля под напряжением. Понижение кривой II относительно кривой 1 объясняется тем, что через диэлектрик шел перед этим измерением ток обратного направления. Разница в показаниях гальванометра при таких измерениях достигает величины до 15%. Если вести измерение сопротивления изоляции одной и той же жилы кабеля сначала постепенно увеличивающимся по величине напряжением, а затем постепенно уменьшающимся, после чего повторить опыт с напряжением обратного знака, то можно получить кривую, аналогичную кривой магнитного гистерезиса. Подобная кривая изображена на фиг. 44.
Сопротивление изоляции сильно зависит и от состава пропиточной массы, в частности, от содержания в массе канифоли. Характер та ой зависимости приведен на фиг. 45 по W. A. Del Маг’у [43]. Эта кривая снималась для смеси петролага (густого нефтяного погона, имеющего консистенцию вазелина) и канифоли. Вопреки общераспространенному мнению прибавка канифоли в небольшом (до 10%) количестве вызывает сильное понижение сопротивления изоляции, при дальнейшем же прибавлении канифоли сопротивление изоляции вновь увеличивается, однако никогда не достигает величины, полученной при чистом петролате.

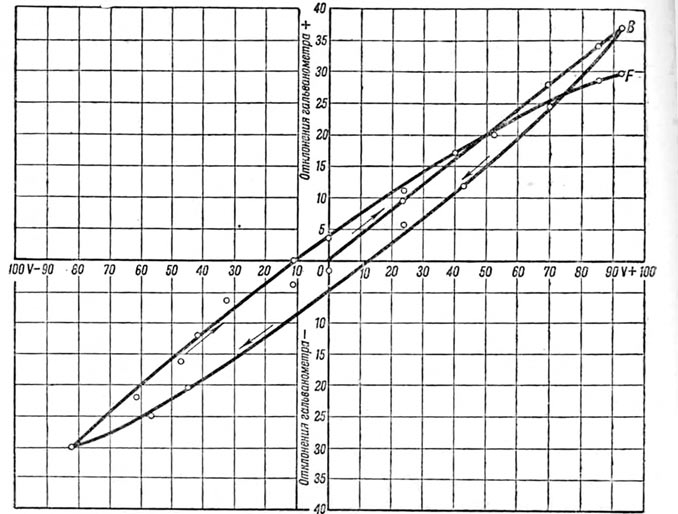
Фиг. 44. Изменение отклонения гальванометра при измерении сопротивления изоляции в зависимости от величины и направления приложенного напряжения.

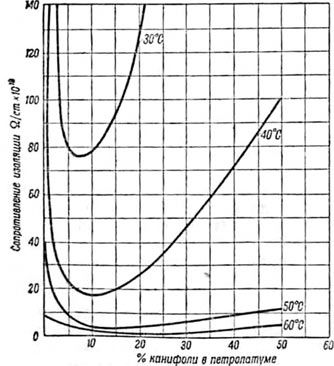
Фиг. 45. Зависимость между сопротивлением изоляции и содержанием канифоли в пропиточной массе по W. A. Del Mat’y.
Подобный же характер согласно работам лаборатории завода „Москабель" имеют кривые зависимости сопротивления изоляции от процентного содержания канифоли в минеральном масле, однако только для предварительно очищенного контактным способом масла. Если же масло предварительно не было химически очищено, то характер кривой несколько меняется: а именно прибавка примерно до 10% канифоли не отражается на величине сопротивления изоляции, а затем сопротивление изоляции начинает увеличиваться.