а) Формула TeiQhmflller’a. Поскольку использование меди кабеля прежде всего зависит от допустимой температуры, то исследование тепловых процессов в кабеле, а следовательно, и допустимого тока нагрузки, является очень важной задачей • кабельной техники. До самого последнего времени допустимый ток нагрузки силовых кабелей вычислялся по формуле проф. J. Teichmtiller’a, основанной на теоретических и практических исследованиях как самого Teichmflller'a, так и проф. G. Mie и P. Humann’a. По этой формуле, например, рассчитана таблица допустимых нагрузок норм VDE. В основном вывод этой формулы опирается на закон Ома в приложении к тепловому состоянию тела:
![]() (87)
(87)
где W — тепловой поток, исходящий из жил кабеля,
т — разность температур между жилами кабеля и окружающей средой;
Sk—тепловое сопротивление кабеля;
Se — тепловое сопротивление почвы, в которой зарыт кабель.
Для кабеля с п жилами сечением каждая Q тепловой поток будет равен
![]() • (88)
• (88)
где p—удельное сопротивление проводникового металла, отнесенное к сечению в 1 мм*, длине в 1 м и температуре, соответствующей перегреву в С.
Рабочая температура для силовых кабелей даже повышена, а именно в формуле вместо 85° С принято 90° С с тем, однако, чтобы рабочая температура жилы не превышала 85° С.
Английский стандарт допускает:
для бронированных кабелей с пропитанной бумажной изоляцией,
проложенных непосредственно в земле .............................................................. 65° С
для небронированных осветительных кабелей в трубах................... 50° С
бронированных 60° С
Таблицы допустимых нагрузок английских норм рассчитаны, исходя из этих температур жилы и температуры окружающей почвы в 15° С.
Бельгийские нормы допускают максимальную температуру жилы кабелей в 60° С.
Итальянские нормы допускают максимальную температуру также в 60° С, а величины допустимых нагрузок высчитаны в этих нормах, исходя из окружающей температуры в 25° С.
Французские нормы допускают перегрев в 30° С, величины нагрузок по этим нормам — наименьшие Из всех норм.
Нагрузки по германским нормам VDE рассчитаны на перегрев меди кабелей с бумажной изоляцией на 25° С сверх температуры окружающей среды, т. е. при 15° С в почве, температура меди по этим нормам не должна быть выше 40° С. Интересно, что для резиновых проводов германские нормы допускают температуру жилы в 50° С, несмотря на то, что резиновая изоляция много менее устойчива в термическом отношении, чем пропитанная бумажная. Нормы эти явились продуктом согласования немецких кабельных заводов и потребителей, причем потребители отстаивали точку зрения увеличения допустимой нагрузки, а кабельные заводы отказывались от гарантии надежности работы кабелей при повышении температуры. До сих пор немецкие заводы не меняют своей точки зрения и еще совсем недавно W. Vogel [122], разбирая вопрос о более высокой по статистике цифре пробоев (в четыре раза) американских кабелей по
сравнению с немецкими, по графе внутренних причин, объясняет это обстоятельство более высокими допущенными у американцев температурами. Однако, очевидно, под влиянием современной экономической обстановки в Германии последние нормы VDE 1934 г. допустили перегрев в 35° С для кабелей до 6 кВ включительно, оставив 25° С для более высоких напряжений.
Допустимые нагрузки по ОСТ 6260 рассчитаны, исходя из окружающей температуры для почвы в 15°С, а воздуха 25°С, при максимальной длительно допустимой температуре жил:

Таким образом в мировой практике стандартизации силовых кабелей длительно допустимые температуры колеблются в диапазоне от 40° С до 85° С.
Влияние температуры на силовые кабели с пропитанной бумажной изоляцией можно рассматривать с двух точек зрения:
- влияние на диэлектрическую прочность и устойчивость электрических характеристик кабеля;
- влияние на химическую и механическую устойчивость изоляции.
Многочисленные исследования показывают, что при быстром поднятии
напряжения диэлектрическая прочность кабеля при высокой температуре скорее возрастает, чем падает, что хорошо вяжется с нашими представлениями о внутреннем вакууме в кабеле, о чем речь будет итти дальше. Однако в результате сильных термических воздействий в кабеле появляется ряд нежелательных явлений, особенно недопустимых в кабелях на рабочее напряжение от 20 кВ и выше. Эти явления заключаются в чрезмерном увеличении диэлектрических потерь в кабеле при высоких температурах, что может повести к тепловому пробою изоляции, а также в остаточном расширении свинцовой оболочки кабеля, что в свою очередь вызывает неустойчивость электрических характеристик кабеля и возникновение ионизации и т. п. Очевидно, что, чем выше напряжение кабеля, тем ниже должна быть рабочая температура его, чтобы сделать устойчивее электрические характеристики. Практика показала, что для кабелей на напряжение свыше 20 кВ температура в 50—60°С должна считаться предельной, если кабель пропитан обычной вязкой массой.
Увеличение толщины изоляции у высоковольтных кабелей на окончательную температуру проводящих жил влияет слабо, ибо при увеличении толщины изоляции увеличиваются и размеры кабеля, что в свою очередь уменьшает его тепловое сопротивление. Но время, требующееся для достижения наивысшей температуры при одном и том же токе, а равно и время, требующееся для охлаждения кабеля, выше у кабелей с более высокой толщиной изоляции, ибо скорость нагрева и охлаждения сильно уменьшается при увеличенной теплоемкости изоляции.
Химическую неустойчивость кабельной изоляции могут характеризовать следующие данные, приводимые Del Маг’ом [12] для составных частей пропитанной бумажной изоляции:
- Для непропитанной бумаги в воздухе разложение начинается при температуре около 140° С, температура вспышки 275° С.
- Для петролата (род вазелина—тяжелый нефтяной погон) разложение на воздухе начинается при 225° С, температура вспышки 375° С.
- Для канифоли разложение на воздухе начинается при 145° С, температура вспышки 335° С, однако, медленное разложение канифоли начинается уже при температурах ниже 100° С.
- Для компаунда, состоящего из 85% петролата и 15 % канифоли, разложение на воздухе начинается при 175°С, температура вспышки 325°С.
Физически высокая температура действует на изоляцию так, что изоляция становится хрупкой. На величину пробойного напряжения это увеличение хрупкости не влияет, но при передвижениях кабеля такая изоляция легко может быть повреждена, в результате чего получится пробой.
В общем нужно сказать, что кабельная изоляция в физическом и химическом отношениях может допускать очень высокий перегрев. Как на пример того, что можно получить в этом отношении, можно указать на исследование D. W. Roper’a [123], который в течение зимних месяцев одного года каждую ночь нагревал кабель до температуры выше 100°С, причем 4 дня в неделю нагрев доходил до 200° С. В одном месте кабель был предварительно освобожден от свинцовой оболочки, и здесь изоляция после окончания опытов стала черной и разрушилась, но несколько отступя, под свинцом бумага стала только коричневой, хорошо сохранила пропитку, но часть механической прочности была ею потеряна. D. W. Roper пришел к заключению, что 110° С не причиняют изоляции разрушения, а 18СРС обязательно ее разрушают. Нужно иметь в виду, что D. W. Roper является представителем эксплуатации и защищает в американских условиях повышение рабочей температуры кабеля. Большой перегрев кабеля очень нежелателен тогда, когда имеются условия, в которых возможна вибрация кабеля: в этих случаях может появиться разрушение свинцовой оболочки от вибраций; такое разрушение особенно легко может возникнуть при температурах свинца выше 80° С.
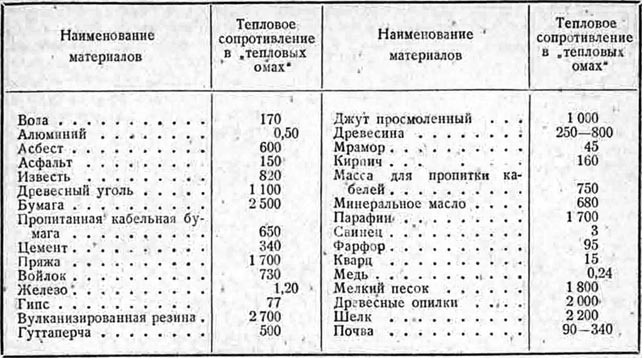
Величина теплового сопротивления кабеля К в практике вычисления допустимых нагрузок также является широко варьирующей величиной. Кроме того, она широко изменяется не только для разных кабелей с одной и той же изоляцией, но даже и для одного и того же кабеля в зависимости от разных условий. Для ряда изолирующих материалов величины теплового сопротивления приведены в табл. 3 по данным фирмы Pirelli.
Del Mar [12] для величины К дает следующие цифры:
Пропитанная кабельная бумага................................................ К= 1 000 до 1200
Вулканизированная резина .................................................................... = 725
Лакированный кембрик......................................................................... = 750
Асфальтированной джут ....................................................................... = 250
Пропитанная бумажная пряжа................................................................ = 750
Цифры Del Маг’а для пропитанной бумаги относятся к старым кабелям, которые, как считают в Америке, были плохо изготовлены. Более современные данные [24] показывают, что крупные американские осветительные компании (NELA) для расчетов теплового сопротивления силовых кабелей с пропитанной бумажной изоляцией берут в среднем 700 "тепловых омов", считая для вновь изготовленных кабелей 500 „тепловых омов“.
Англичане принимают для кабелей с рабочим напряжением До 2 200 В К= 750, а для кабелей с рабочим напряжением выше 2 200 В К = 550. Такой разницей англичане учитывают более совершенную пропитку кабелей, построенных на высокое напряжение.
Нормы Союза германских электротехников (VDE) рассчитаны на К=550, ОСТ 6260 — также на К=550.
Riley и Scott [71], производившие большие исследования термических свойств английских кабелей, нашли, что на свеже изготовленных кабелях К колеблется от 300 до 1 300 "тепловых омов".
Согласно Riley и Scott [71] на величину теплового сопротивления кабеля влияют следующие факторы:
- Степень сушки кабеля. Чем хуже высушен кабель во время производства, тем меньше его тепловое сопротивление.
Однако плохая сушка кабеля является источником потерь энергии в диэлектрике, в особенности при высоких температурах, что снижает допустимую нагрузку током по другой линии.
- Степень пропитки кабеля. Чем лучше пропитан кабель, тем ниже его тепловое сопротивление. Этот фактор является одним из наиболее важных для улучшения тепловых характеристик кабеля и в то же время он является основным фактором для улучшения его физических и электрических характеристик.
Тепловое сопротивление различных материалов по данным фирмы Pirelli
- Плотность намотки бумаги на жилу. Тугая намотка бумаги также уменьшает тепловое сопротивление и также одновременно улучшает электрические характеристики кабеля.
- Конструкция кабеля и его геометрические размеры. Конструкция кабеля также оказывает значительное влияние на тепловое сопротивление, например, по сравнению с обычным кабелем с поясной изоляцией и при одинаковом наружном диаметре кабеля, так называемые Н-кабель и ОСБ-кабель имеют тепловое сопротивление на 10—15% ниже. Секторные кабели при одинаковой площади сечения проводящих жил и одинаковых толщинах изоляции имеют тепловое сопротивление на 4—6% ниже, чем кабели с круглыми жилами.
- Качество изоляции. Качество пропиточной массы не оказывает большого влияния на тепловое сопротивление. По-видимому, величина теплового сопротивления изменяется обратно пропорционально плотности массы. Канифоль слабо повышает тепловое сопротивление. Более плотная бумага имеет более низкое тепловое сопротивление, чем менее плотная.
- Температура кабеля. С увеличением температуры тепловое сопротивление кабеля падает. Riley и Scott нашли, что тепловое сопротивление испытанного ими кабеля с 850 „тепловых омов" при 20° С упало до 520 „тепловых омов“ при 60°С. Этот эффект, вероятно, обязан своим существованием высокому коэффициенту температурного расширения для пропиточной массы, вследствие чего при повышенной температуре объем пустот в кабеле, имеющий большое тепловое сопротивление, становится меньше, чем при низких температурах.
- Повторяемость циклов нагрева. Повторяемость циклов нагрева увеличивает тепловое сопротивление кабеля, иными словами, находившиеся в эксплуатации кабели имеют более высокое тепловое сопротивление, чем свеже изготовленные. В одном случае Riley и Scott нашли увеличение теплового сопротивления хорошо пропитанного кабеля с 350 до 520 „тепловых омов“ после восьми циклов нагрева. Это явление обусловливается, вероятно, остаточной деформацией свинцовой оболочки кабеля после избыточного давления массы при нагреве кабеля, благодаря чему в кабеле образовываются имеющие высокое тепловое сопротивление пустоты. Величина этого увеличения стремится к некоторому определенному пределу.
Еще более, чем величина теплового сопротивления кабеля, варьирует величина теплового сопротивления почвы Н. Она зависит от рода почвы, ее влажности, способа и глубины прокладки и т. п. Нормы допустимых нагрузок по VDE рассчитаны на Н= 40 тепловых омов. Это — наименьшая величина из всех имеющихся норм. Для ОСТ 6260 принята величина Н= 80 тепловых омов. Допустимые нагрузки по английскому стандарту рассчитаны на Н=180, причем для разных видов прокладки приведен ряд поправочных коэффициентов. Японские нормы рассчитаны на Н=380; это —наивысшая величина по всем имеющимся нормам. Del Маг [12] по P. Torchio дает следующие величины для теплового сопротивления почвы:

В американской практике к тепловому сопротивлению почвы обычно прибавляется еще тепловое сопротивление доктовых линий (кабельная канализация).
Наиболее подробно вопрос о тепловом сопротивлении почвы освещен в английском стандарте, основанном на тщательных и многосторонних исследованиях S. W. Melsom’a и Е. Fawsett’a [124]. Этот стандарт дает следующую таблицу тепловых сопротивлений почвы разного рода:

Так как таблица нагрузок по -английскому стандарту рассчитана для Н= 180, то в нем имеется следующая таблица поправочных коэффициентов для разных тепловых сопротивлений почвы, которой можно пользоваться для кабелей и не английского происхождения, если пересчитать ее на то тепловое сопротивление почвы, которое принято для соответствующего стандарта:![]()
Глубина прокладки также влияет на величину допустимой нагрузки током, а именно, чем глубже зарыт, кабель, тем теоретически меньше допустимая нагрузка, ибо тем хуже отвод тепла поверхностью земли. По данным английского стандарта при 18 дюймах глубины прокладки можно допустить величину тока на 9% выше, чем при 54 дюймах, но при этом сделана оговорка, что на практике это преимущество в значительной степени устраняется тем, что в теплое время года почва вблизи поверхности земли более подвержена осушению и нагреву, чем в глубине.
На величину теплового сопротивления почвы оказывает также влияние и способ прокладки кабеля. По опытам BEWAG в Берлине [125] для разных родов прикрытия кабеля получаются следующие величины нагрузок одного и того же кабеля в процентах:
Песок . ........................................................................................ 100 %
Бетонный панцирь (заделка 7 см.)............................................ 96 %
Кирпич (обычное прикрытие).................................................... 94 %
Прикрытие из формованного углом бетона............................. 85 %
Железная труба......................................................................... 79 %
На величину теплового сопротивления почвы влияет также и продолжительность нагрева почвы кабелем благодаря постепенному осушению почвы; вопрос этот, однако, не обследован.
При всем разнообразии выбора величин разными стандартами в величинах допустимых токов нагрузки разных стран наблюдается значительно меньшее разнообразие, хотя оно все-таки достаточно велико, как это видно из нижеследующего сравнения допустимых нагрузок по разным нормам для кабеля марки СБС сечением 3x150 мм2, 1 000 V. В этом сравнении нагрузка по нормам VDE 1927 г., соответствующая нашим прежним нагрузкам по нормам ВЭС, принята за 100 %:

В этом сопоставлении цифры для американских норм даны для случая прокладки в канализации. Так как этот метод прокладки вызывает дополнительный нагрев кабеля, то для случая прокладки в земле американцы допускают более высокую нагрузку. Судя по данным NELA [24], это повышение следует оценить в 22%, поэтому допустимая нагрузка по нормам NELA в этом случае будет 309-1,22 = 377 А, или 116 % от норм VDE 1927 г. Однако те же публикации NELA рекомендуют пользоваться так называемой "консервативной нагрузкой", т. е. выбирать ближайшее большее сечение, считая это „всегда разумным вложением". В таком случае допустимая нагрузка по нормам NELA будет 338 А, или 104 % от норм VDE 1927 г.
Данные итальянской фирмы Pirelli, являющейся одной из наиболее авторитетных мировых кабельных фирм, вычислены, исходя из К= 750, что фирма считает констатированным для изоляции ее кабелей [31]. Для джутовой оболочки поверх свинцовой та же фирма дает 800 „тепловых омов"; при наличии железной брони, которая является хорошим проводником тепла, она дает 600 „тепловых ом“. Величина теплового сопротивления почвы по данным этой фирмы Н=100.
При этом сравнении бросается в глаза сильно завышенная цифра нагрузки по ОСТ 6260. Нагрузка в сетях Мосэнерго часто достигает таких величин, которые стандартизированы ОСТ 6260, однако именно этим обстоятельством, вероятно, объясняются винтообразные оттиски на свинцовой оболочке кабелей, которые часто наблюдаются на старых кабелях из сетей Мосэнерго. Такие же оттиски, впрочем, могут появляться и в результате коротких замыканий.
Следует иметь в виду, что увеличение использования меди путем допущения увеличенной нагрузки влезет за собой значительное увеличение потерь на джоулево тепло. Экономические подсчеты показывают, что обычно увеличение нагрузки с экономической точки зрения далеко не выгодно. В частности, в наших условиях все сбережения, сделанные на меди, благодаря увеличению нагрузок по ОСТ 6260 истрачиваются не более, чем в 2 года на увеличение расхода топлива.
Ь) Метод D. Simmons’a. При вычислениях емкости, допустимого тока нагрузки или сопротивления изоляции приходится считаться с двумя родами величин: не зависящих от геометрических размеров кабеля и зависящих только от них. Второй род величин, являющихся константами для данного типа кабеля и введенных в одну формулу, принято в Америке называть геометрическими коэффициентами. О значении геометрических коэффициентов при вычислениях емкости мы уже говорили выше. Для случая вычисления допустимого тока нагрузки формулу (89) можно изобразить в виде
![]() (94)
(94)
где G, — геометрический коэффициент.
Геометрический коэффициент зависит от схемы включения многожильных кабелей, для одножильных кабелей он остается постоянным для всех случаев вычислений. В формуле Teichmiiller’a, поскольку она использует не действительные, а приведенные к идеальному однородному _ кабелю величины, геометрические коэффициенты кабелей несколько отличаются от выведенных для вычисления емкостей. Tеichmflller использовал для своей формулы данные G. Mie, в Америке и Англии для такого рода вычислений более популярны выражения, данные Russell’eM. D. Simmons [63] дал метод вычисления нагрузок, исходя из действительных геометрических коэффициентов и расчленил тепловое сопротивление кабеля на отдельные части. Для этой цели он сначала сделал сравнение величины G, получающейся из формул G. Mie и RusseU’H, с величинами, вычисленными на основании экспериментальных данных R. W. Atkinson’a, которые он ввиду тщательности и точности выполнения эксперимента принял за точную картину, имеющуюся в действительности. Simmons нашел с этой точки зрения, что наиболее правильными являются величины, получающиеся из формул Mie, поэтому весь дальнейший расчет допустимых нагрузок он вел, опираясь, главным образом, на данные G. Mie. Прежде всего Simmons задался целью определения графическим путем величин ошибок, получающихся из формул G. Mie по сравнению с экспериментальными величинами Atkinson’a. G. Mie при выводе своей формулы пользовался „заменяющей фигурой", так же, как и Russell, однако эти фигуры у обоих авторов были разные.

21. Часть заменяющей фигуры О. Mie.
Часть такой заменяющей фигуры Mie для случая трехжильного кабеля изображена на фиг. 21 линией abc. Для T+t t
определенного отношения —^— и у ,
где t—радиальная толщина поясной изоляции; Т—радиальная толи.ина изоляции на жиле; d— диаметр медной жилы, Simmons строил фигуру
Mie, именно — часть полной окружности, делил ее на 18 частей, затем строил проводящие трубки так, как указано на фиг. 21, и промерял средние пути этих трубок до заменяющей фигуры и до жилы. Отношение получающейся величины Пути до жилы к величине пути до заменяющей фигуры будет поправкой на проводимость трубки. Общая проводимость всего отрезка кабеля будет суммой проводимостей отдельных трубок, причем истинная проводимость кабеля будет всегда меньше проводимости до фигуры Mie. Если теперь вычислить для этого кабеля G, по Mie и умножить полученную величину на отношение .проводимостей, т. е. на поправочный коэффициент, то мы получим правильную величину О,. На основании таких вычислений Simmons дал ряд эмпирических формул для определения G,, точность которых колеблется от 0,5 до 1,2%.
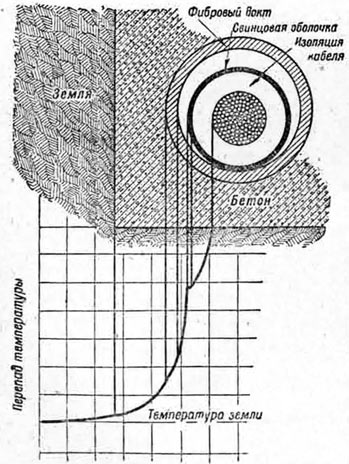
Фиг. 22. Диаграмма перепада температур в работающем кабеле по американским данным (NELA).
Для оценки перепадов температуры при прокладке в доктах на фиг. 22 дана диаграмма, заимствованная из данных NELA [24].
с) Допустимая нагрузка кабелей с металлизированными жилами. Вышеприведенные формулы не дают возможности вычислить допустимые величины тока для кабелей с металлизированными жилами, т. е. для таких трехжильных кабелей, у которых каждая изолированная жила имеет свою отдельную металлическую оболочку (подробное описание конструкции см. в отделе III „Конструкция кабелей"). Благодаря наличию на жилах этих кабелей металлической оболочки, облегчающей отвод тепла от центра кабеля, допустимая нагрузка для таких кабелей выше, чем для обычных кабелей с поясной изоляцией. К этому добавляется то, что у таких кабелей проводящие жилы расположены ближе к общей металлической оболочке, чем у кабелей с поясной изоляцией, что также облегчает условия охлаждения. Эти обстоятельства дают возможность в среднем увеличения у кабелей с металлизированными жилами допустимой нагрузки на 5—15% по сравнению с кабелями с поясной изоляцией.
В настоящее время существует несколько способов теплового расчета подобных кабелей, как, например, С. Feldmann’a [51], D. М. Simmons’a , С. М. Брагина [38], Fock’a и др. Мы здесь опишем как наиболее употребительный метод Simmons’a, отметив, что этот способ по подсчетам Брагина дает очень близкие результаты к вычислениям по методу Брагина.
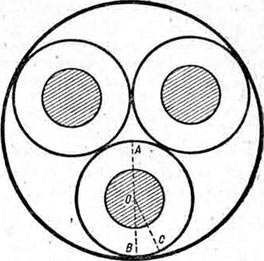
Фиг. 23. Принципиальная схема экранированного кабеля.
Способ Simmons'a относится к так называемым Н-кабелям, т. е. к кабелям, у которых поверх трех металлизированных жил имеется общая свинцовая оболочка (кабели типа ОСБ, т. е. с отдельно освинцованными жилами, в Америке не делаются из-за принятого там способа прокладки в доктах). Весь вопрос о расчете допустимой величины тока, как мы видели выше, сводится к вычислению теплового сопротивления кабеля Sk или обратной ему величины тепловой проводимости Ак. Simmons исходил из предположения, что тепловой поток из жил кабеля переходит по металлизирующей оболочке (экрану) к общей свинцовой оболочке и что тепловой проводимостью прокладки между жилами можно пренебречь. На фиг. 23 приведена принципиальная схема такого кабеля. Переход тепла от жилы по экрану идет двумя путями: а) по дуге ВС так, как у одножильных кабелей, и б) по дуге АС в точке С, где кончается прилегание общей свинцовой оболочки к экрану.

