Представим себе цепь электрического тока, состоящую из прямого и обратного одножильных кабелей (фиг. 8). Напряжение магнитного поля Н в любой точке М кабеля на расстоянии от оси проводящей жилы кабеля, как показывается в теории поля, будет направлено в плоскости, перпендикулярной оси кабеля и перпендикулярно к радиусу, проведенному через точку М, причем величина этого напряжения будет равна
![]() (33)
(33)
где i — ток в жиле кабеля.
Для коэффициентов самоиндукции секторных кабелей нет формул, основанных на теоретических выкладках, но согласно D. Simmons’y [108] этот коэффициент может быть с достаточной степенью точности определен, если для величины D в формуле (55) будет взято расстояние между серединами
![]()
Фиг. 11. Схема течения токов Фуко в толще провода.
радиусов секторов.
В американских Н-кабелях, имеющих вокруг трех металлизированных жил скрепляющую ленту из магнитного материала, коэффициент самоиндукции согласно Simmons’y будет значительно выше теоретической величины, а именно он по опытным данным превышает вычисленную величину на 10—20%.
К электромагнитным явлениям относится также и явление, носящее название скин-эффекта, или поверхностного уплотнения тока, возникающего вследствие токов Фуко, индуктирующихся в толще провода. Представим с бе продольное сечение жилы кабеля (фиг., 11). Пусть стрелка на оси XX указывает на направление основного тока в данный момент времени. Этот ток в толще проводника будет индуктировать токи Фуко того направления, которое указано на фиг. 11. Направление токов Фуко определится тем, что возбуждаемый ими магнитный поток должен противодействовать магнитному потоку основного тока. Из фиг. 11 видно, что паразитные токи по периферии провода будут иметь то же направление, что и основной ток, а внутри провода—противоположное направление. В результате получается увеличение электрического сопротивления провода и неравномерная плотность тока по сечению провода.
Увеличение электрического сопротивления пропорционально частоте переменного тока и площади поперечного сечения провода. Для обычной промышленной частоты 50 Hz и при диаметре провода не свыше 15 мм увеличение сопротивления выражается величиной около 2%, при диаметрах же около 10 мм—0,01%. Поэтому практически с таким увеличением сопротивления можно не считаться, однако необходимо иметь в виду, что для очень больших сечений увеличение сопротивления провода от влияния скин-эффекта может достичь очень значительной величины, так, например, при 50 Hz и 800 мм2 сечения, когда диаметр жилы достигает 36 мм, увеличение достигает 30%.
В технике передачи энергии с помощью высоковольтных кабелей встречаются случаи употребления кабелей с сечением жилы до 500—800 мм, например, для соединения генераторов с повысительными трансформаторами на крупных центральных электрических станциях. В этих случаях влияние скин-эффекта очень значительно, так что часто прибегают к искусственным мерам для снижения влияния этого эффекта. Эти меры заключаются в том, что или делают жилу с сердечником из волокнистого материала, например, из веревки, или подразделяют жилу на отдельные части, скручивая ее из изолированных трех или четырех секторов. Первый способ сильно увеличивает диаметр кабеля и поэтому дорог, второй способ много выгоднее.
Коэффициенты увеличения омического сопротивления проводов k в зависимости от диаметра провода d и частоты

В Англии недавно запатентован кабель, носящий название „Milliken- segmental“—кабель, который скручивается из трех или четырех секторов с легкой изоляционной между ними прокладкой [114]. Скин-эффект в таком кабеле понижается до величины, которую он имеет для сечения в одну четверть или одну треть от общего сечения жилы. Явление уменьшения скин-эффекта приписывается выравниванию индуктивного сопротивления жилы благодаря транспозиции большего числа индивидуальных проволок в каждом секторе. У нас также в большом количестве делались кабели, скрученные из трех секторов с изоляцией на 1 000 В и с общей поясной изоляцией на 10000 V, эти кабели служили, как одножильные кабели в трехфазной системе на 10000 V. Помимо выигрыша в омическом сопротивлении такие кабели выгодны и в смысле гибкости.
Для определения возрастания омического сопротивления жил вследствие скин-эффекта можно пользоваться табл. 2, составленной по данным Kelvin’a и Hospitaller. В этой таблице f—частота в герцах; d — диаметр провода в сантиметрах; k = — отношение омического сопротивления при переменном токе Rw к омическому сопротивлению при постоянном токе Rg. Таблица пригодна только для проводов сплошного сечения (без джутового сердечника), изготовленных из немагнитных материалов.
В практике назначения толщин изоляции силовых кабелей нашло свое отражение все вышесказанное. Кабели низкого напряжения до 3 кВ включительно электрическому расчету не подвергались, так как их изоляция всегда рассчитывалась только на механическую прочность, поскольку запас электрической прочности у этих кабелей очень велик. Для кабелей более высокого напряжения довоенные нормы VDE, которыми руководствовались и наши заводы, толщины изоляции кабелей с тонкими жилами назначались выше, чем для кабелей с толстыми жилами. Тот же принцип был удержан нормами VDE при пересмотре их в 1922 г., несмотря на то, что толщина изоляции вообще была снижена приблизительно на 30%. Впервые в 1927 г. в нормах VDE появились равные толщины изоляции как у кабелей с тонкими, так и толстыми жилами. Поэтому у современных кабелей с тонкими жилами рабочий градиент напряжения значительно выше, чем у кабелей с толстыми жилами. В английских нормах [28] последнего издания (1933 г.) для кабелей среднего напряжения в 6, 10 и 20 кВ для очень больших сечений, начиная с 0,4 кв. дюйма, толщины изоляции даже повышены по сравнению с малыми сечениями. Зависимость между рабочими градиентами и сечениями кабелей для новых английских кабелей дана на фиг. 15 (по P. V. Hunter’y) [116], эти кривые указывают на то, как мало теперь считаются с увеличением рабочего градиента у кабелей с тонкими жилами. Для кривых фиг. 15 расчет был сделан для напряжения до 22 кВ включительно на кабели, имеющие толщины изоляции по последним английским нормам, а для более высоких вольтажей принята обычная английская практика толщины изоляции, а именно 0,325 дюйма для 33 кВ и 0,65 дюйма для 66 кВ. Фиг. 15 обращает внимание на то, что, чем выше рабочее напряжение кабеля, тем выше его рабочий градиент. Казалось бы, что следует делать наоборот, однако при этом размеры кабеля столь сильно возрастают, что кабели стали бы совершенно не экономичными и крайне неудобными. Поэтому, чем выше рабочее напряжение, тем ниже относительный запас электрической прочности высоковольтного кабеля. Так как процесс изготовления, а равно и качество материалов для хорошо изготовленных кабелей высокого и среднего напряжения отличается сравнительно не сильно, а к кабелям среднего напряжения вполне может быть применен процесс изготовления кабеля высокого напряжения, то в целях экономии материалов нет принципиальных доводов против применения повышенных напряженностей и для кабелей среднего напряжения.

Фиг. 15. Зависимость между сечениями и градиентами напряжения последних английских стандартных кабелей по P. V. Hunter’y.
Согласно этой идее в Англии были сделаны опытные кабели по размерам 22-кВ кабелей, которые были пущены в эксплуатацию при 33 кВ, причем при изготовлении кабелей был применен технологический процесс, употребляемый для кабелей на 66 кВ, градиент опытных кабелей был равен 5,16 кВ/мм; они работают вполне успешно [116]. Этот пример показывает, что и для кабелей среднего напряжения предел снижения толщин изоляции еще не перейден, однако дальнейшее снижение может идти только за счет улучшения качества изоляционного материала, в особенности в отношении его механической прочности.
Понятие о величине запаса диэлектрической прочности кабеля является одним из важнейших понятий в области практики кабеля, так как этот запас в значительной степени определяет как надежность эксплуатации кабеля, так и его надлежащую экономичность. Определение запаса диэлектрической прочности кабеля не является вполне простой вещью, хотя бы по одному тому, что ни один идущий в дело барабан кабеля нельзя доводить до пробоя. Можно отличать понятие о действительной прочности кабеля от понятия о среднем запасе прочности, если считать на так называемое мгновенное, т. е. не более 1—5 мин. по времени приложения, пробойное напряжение. Для старых кабелей, когда этим вопросом очень интересовались, поданным М. Klein’a [117 и 118] такой запас при условии принятия специальных мер предосторожности во время изготовления колебался на 40-50% от средней пробойной величины, а по данным М. Hochstadter’a [45] — только на ± 10% для обычной торговой продукции. Наши новые кабели, судя по результатам испытаний на отрезках кабелей, скорее приближаются к данным Hdchstadter’a, чем к данным Klein’a.
Теперь, однако, на мгновенное пробойное напряжение обращают очень небольшое внимание, так как по величине мгновенного пробойного напряжения нельзя судить о качестве кабеля, ибо при длительно приложенном напряжении пробойная прочность сильно снижается и притом далеко не одинаково для разных кабелей. Для отношения пробойного напряжения при длительном его приложении к моментальному пробойному напряжению F. W. Реек [98] дает следующую формулу:
![]() (78)
(78)
где k — отношение пробойного напряжения при его длительном приложении к моментальному, причем моментальным пробоем считается такой пробой, когда кабель пробивается через 30 сек. или менее;
Т—время до пробоя в секундах;
а — постоянная для данного типа кабеля.
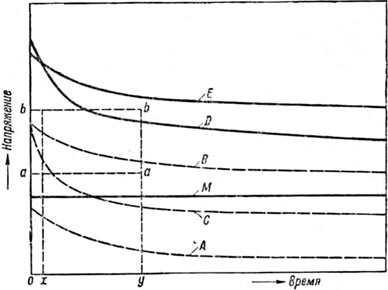
Фиг. 16. Интерпретация кривых жизни кабеля по F. М. Farmer’y.
По W. A. Del Маг’у и С. F. Hanson’y [43] для американских кабелей определенная опытным путем величина а = 0,42. Если в формуле (78) положить Т равным очень большой величине, то £ = 0,42, т. е. для американских стандартных кабелей теоретическая величина напряжения, при котором кабель никогда не пробьется, составляет около 42% от величины пробоя при моментальном подъеме напряжения. У хорошо изготовленных кабелей, в особенности у маслом наполненных кабелей, величина а значительно выше.
В настоящее время суждение о качестве кабеля с точки зрения его запаса пробойной прочности девается по так называемой "кривой жизни". Эта кривая представляет собой снятую экспериментальным путем зависимость пробойного напряжения от времени приложения напряжения. Снятие этой кривой делается таким образом, что куски одного и того же кабеля, длиной каждый около 5—10 м, ставятся под различное напряжение и отмечается время, через которое каждый кусок пробьется, затем по данным опыта строится кривая зависимости пробойного напряжения от времени его приложения. На фиг. 16 приведена схема характеристик, получаемых при такого рода измерениях по F. М. Farmer’y [119]. Прямая М представляет рабочее напряжение, на которое рассчитан кабель, линии аа и bb — различные испытательные напряжения. Если в кабеле имеется слабое место, которое в зависимости от времени приложения напряжения давало бы кривую жизни А, то при приложении умеренного испытательного напряжения аа кабель был бы пробит. Если дефект менее интенсивен, то он дает кривую жизни В, причем испытательное напряжение аа его не обнаружило бы, а испытательное напряжение bb обнаружило бы его моментально. Кривая С получается при другом возможном повреждении. Кабель без дефектов может иметь кривую жизни Е или D, первая, конечно, предпочтительнее, несмотря на то. что мгновенное пробойное напряжение в этом случае ниже, чем в случае кривой D. В современных кабелях стремятся к получению возможно более плоской кривой жизни. Понятно, что эти испытания принадлежат к числу типовых и как таковые не могут делаться на всех кабелях.
Согласно Hоchstadter’y и Barrat [120] характер зависимости пробойного напряжения от времени его приложения можно выразить математически, если предположить, что мы имеем дело только с тепловым пробоем, а не с пробоем, зависящим от дефектов в изоляции. При включении напряжения диэлектрик кабеля будет нагреваться потерями в диэлектрике до тех пор, пока не возникнет состояние устойчивого равновесия между возникающим в диэлектрике и отводимым теплом. Для некоторого определенного момента времени тепловое состояние кабеля может быть выражено следующим уравнением:
![]() (79)
(79)
где р — потеря мощности в диэлектрике;
в —температура диэлектрика;
А—теплоемкость кабеля;
В — коэффициент теплопроводности верхней поверхности кабеля;
t— время.
Время, необходимое для достижения некоторой температуры, выразится из уравнения (79) следующим образом:
![]() (80)
(80)
Решение этого уравнения может быть сделано графически следующим образом:
На фиг. 17 нанесены кривая потерь 1 и прямая теплоотдачи 2 как функции температур жилы для одножильного кабеля сечением 150 raм2 и 60 кВ рабочего напряжения при максимальной напряженности 24 кВ/мм и температуре испытания в 15° С.
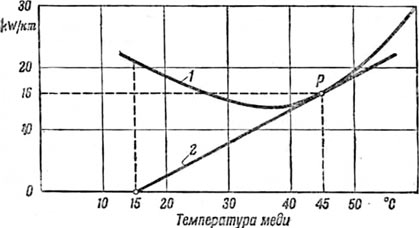
Фиг. 17. Диаграмма устойчивости теплового режима кабеля по М. Hodistadter'y.
В точке р достигается тепловое равновесие, причем температура жилы кабеля будет 45° С, т. е. повысится на 30° С. Точка р отвечает значению бесконечности для кривой зависимости пробойного напряжения от времени. Если кривая 1 опускается, т. е. если градиент напряжения, от которого зависят потери в диэлектрике, уменьшается, то она пересечет прямую 2, и получится устойчивая работа кабеля. При повышении кривой 1, наоборот, тепловое равновесие вообще будет невозможно и кабель рано или поздно будет пробит.
С точки зрения этой теории Hоchstadter делает следующие выводы:
- так как кривая теплоотдачи зависит от состояния вне кабеля, то она не может рассматриваться как вполне определённая характеристика кабеля;
- тепловые явления имеют величайшую важность для надежности кабелей в эксплуатации.

