В настоящее время существует тенденция применения более сложных математизированных подходов [2, 78—92]. Коснемся состояния дел и перспектив численного моделирования процессов сгорания с использованием точного описания дифференциальными уравнениями в частных производных процессов переноса тепла, массы, количества движения и других величин. Экономичность конструирования, эффективность разработки и эксплуатации значительно увеличиваются, если имеется возможность предварительного расчета поля течения на осиone математической модели, включающей процедуру численного интегрирования. Тогда результаты можно получить с меньшими затратами, быстрее и точнее, чем другими способами (например, при проведении экспериментов на реальных системах или на моделях). В общем случае для систем сжигания жидкого топлива интерес представляет следующее:
- влияния и тенденции;
- характеристики камеры сгорания и т. п.;
- оптимальный угол распыления топлива, интенсивность закрутки, форма обтекателя и т. п.
Чтобы обеспечить получение этих данных, модель должна давать информацию о всех важных аспектах течения (геометрические характеристики, граничные условия, физические свойства газов, турбулентность, сгорание и т. п.) и обеспечивать возможность решения уравнений. Основные элементы такого метода показаны на рис. 1.14 Математические модели, все более приближающиеся к реальности и дающие все более подробную информацию, развиваются как по пути увеличения размерности модели (вместе с методами численного решения), так и более точного описания протекающих физических процессов. Ясно, что трудности связаны с двумя аспектами: моделированием и решением.
Численные методы расчета течений в камерах сгорания (которые представляют собой трехмерные турбулентные реагирующие течения) имеют два существенных основания: математические модели физических процессов (турбулентность, излучение, горение и эффекты двухфазности) и компьютерные программы решения получающихся дифференциальных уравнений соответствующего уровня сложности (0-, 1-, 2- и 3-мерный подходы). Каждая из этих частей имеет свои конкретные случаи применения и свои ограничения. Свойства течения могут описываться параболическими уравнениями (типа пограничного слоя) или чаше эллиптическими (течения с обратными токами), и в зависимости от этого схема решения оказывается различной. Слабо закрученные струи и пламена без осевой рециркуляционной зоны относятся к течениям первой категории. В камерах сгорания чаше всего образуются течения с сильно искривленными линиями тока и возникают рециркуляционные зоны (например, угловые рециркуляционные зоны) даже в отсутствие закрутки, и такие течения относятся ко второй категории.
Таблица 12. Система дифференциальных уравнений для трехмерного диффузионного пламени
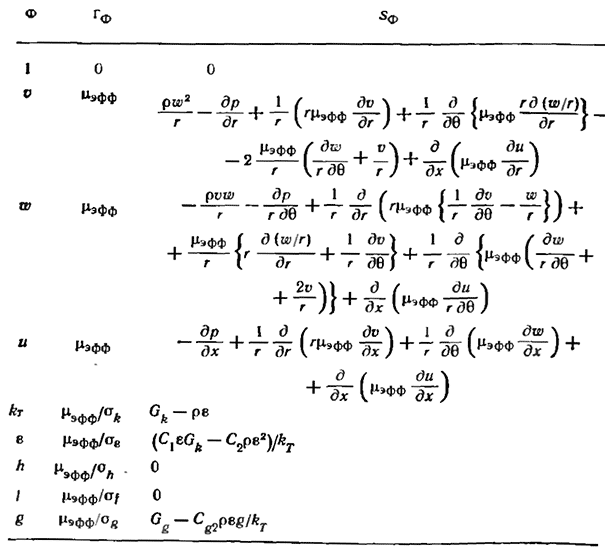
Ясно, что и сильно закрученные течения, в которых закрутка достаточно велика для образования центральной тороидальной рециркуляционной зоны, относятся ко второму, т. е. эллиптическому, типу. В любом из случаев (параболическом или эллиптическом) многие подходы начинаются со следующих основополагающих идей [78], представленных для полностью трехмерного поля течения, из которого можно легко вывести формы моделирования меньшей размерности [2].
Система уравнений Рейнольдса для турбулентного течения, представляющая собой совокупность уравнений сохранения массы, количества движения, энтальпии торможения и химических компонент, может быть упрощена в соответствии со сложностью рассматриваемой реакции в зависимости от того, рассматривается ли диффузионное пламя или горение при предварительном перемешивании, и от того, каков уровень используемой для замыкания модели турбулентности. При использовании предположения о существовании коэффициента турбулентного обмена стационарные уравнения в трехмерных цилиндрических полярных координатах будут иметь вид
![]()
где Ф — зависимая переменная, а соответствующие значения Гф и Sф приведены в табл. 1.2. Здесь использованы следующие обозначения
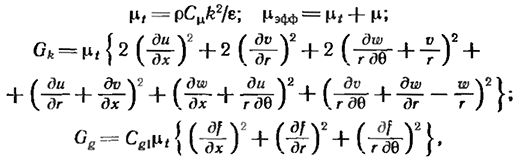
и эта система уравнений описывает трехмерное диффузионное пламя с участием лишь двух компонентов — топлива и окислителя. Уравнения могут быть решены относительно Ф, равного, например, осевой, радиальной и окружной скоростям и, v, w, энтальпии торможения ft, массовой доле избытка окислителя в смеси окислитель — топливо f= тox—smfu, где s — стехиометрическое массовое отношение окислитель/топливо, кинетической энергии турбулентности на единицу массы кт, скорости диссипации ε и среднему квадрату пульсационной компоненты концентрации g = f'2. Если моделировать эффекты излучения и (или) наличие капель жидкого топлива, то нужны дополнительные соотношения. Другие усложнения появляются при учете эффектов, имеющих место в турбулентном потоке вблизи стенок, где для адекватного воспроизведения распределения параметров в логарифмической области без введения слишком мелкого разбиения расчетной сетки рекомендуется использовать пристеночные функции Для входящих в уравнения констант обычно используются рекомендуемые значения [78]: постоянные в kT — ε модели: С1 = 1,44;
С2 = 1,92; σε = 1,0; σk = 1,3; Сμ = 0,09;
постоянные модели для g: Сg1 = 2,8; Cgg2 = 2,0; эффективные значения чисел Прандтля и Шмидта
σh = 0,7; σf = 0,7; σg = 0,7.
Решение этих дифференциальных уравнений вместе с несколькими алгебраическими уравнениями позволяет получить параметры представляющего интерес поля течения. Это моделирование может быть более сложным при рассмотрении реакций предварительно перемешанной смеси (решая дополнительно уравнение для массовой доли топлива т1и и включая скорость химической реакции Rfu) или менее сложным (в случае диффузионного горения в камере только с двумя потоками на входе (топлива и окислителя) нет необходимости решать уравнение для h, когда стенки являются адиабатическими, нереагирующими и непроницаемыми).
Достижение замкнутости и полноты системы уравнении осуществляется с помощью моделей физических процессов, протекающих в системе с горением. Степень подробности описания этих процессов обычно ограничивается либо нашими знаниями о процессе, либо вычислительными возможностями используемой ЭВМ. Необходимо моделировать четыре основных процесса:
1. Турбулентность, где используются модели с уравнениями для коэффициентов турбулентного обмена или непосредственно для турбулентных напряжений в случае закрученных течений. В настоящее время рекомендуются модели с уравнениями для энергии и масштаба длины, в частности kT — ε-модель, где ε= k'/'l, а l — интегральный масштаб турбулентности.
2. Радиационный перенос, где интегродифференциальные уравнения могут быть представлены «зонным методом», или одним из «методов потоков» для одной, двух или трех сумм потоков. (Зонный метод более точный, но его сложнее использовать вместе с уравнениями гидродинамики; метод потоков менее точный, но его легче использовать.)
3. Химические реакции, включая моделирование предварительно перемешанных и диффузионных пламен, сложные уравнения, описывающие образование загрязняющих веществ, методы описания «жесткой» кинетики (где для сильно отличающихся коэффициентов скорости реакции требуются специальные методы представления неоднородных слагаемых) и влияние структуры турбулентности на средние по времени скорости химических реакций. Правильное описание сложных химических реакции в турбулентных реагирующих потоках является, вероятно, той частью моделирования камер сгорания, исследование которой наиболее актуально и результаты которой могут оказаться чрезвычайно полезными для практических приложений.
4. Явления, связанные с двухфазностью, для частиц твердого и капель жидкого топлива, включая предположение о бесконечном коэффициенте сопротивления для мелких частиц и использование обыкновенных дифференциальных уравнений для траекторий более крупных частиц, а также исследование скорости горения капель, облаков и аэрозолей.
Отметим, что все уравнения сохранения аналогичны уравнениям для ламинарных течений, но переменными являются осредненные по времени значения и потоки количества движения, энтальпии торможения и химических компонент, состоящие из двух частей: ламинарной и турбулентной, причем последняя связывается с корреляциями турбулентных пульсаций. Они должны описываться некоторой моделью турбулентности по аналогии с законами Ньютона, Фурье и Фика для ламинарных течений с использованием коэффициентов турбулентного обмена, связывающих потоки с локальными градиентами, а также чисел Прандтля, Шмидта, rθ-компонент вязкости и других для выражения связи других коэффициентов обмена с первичной компонентой турбулентной вязкости μ.
В теории турбулентности изотропия представляет собой термин, подразумевающий в качестве следствия существование скалярной турбулентной вязкости в точках ноля течения. Если турбулентная вязкость не одинакова для различных скоростей деформаций по разным направлениям, то используется представление о неизотропии, и связь других компонент с первичной компонентой турбулентной вязкости выражается через rθ-компоненту и другие компоненты вязкости по аналогии с числами Прандтля и Шмидта.
Численные методы расчета
Существенная разница между программами расчета на ЭВМ обусловлена различием сложности системы уравнений для моделирования физических процессов, требований к объему памяти, распределения переменных в системе пространственных ячеек, методов вывода конечно разностных уравнений и методов их решения. При записи уравнений в естественных переменных давление — скорость обычно используется система с расположением узлов ячеек в шахматном порядке в соответствии с рекомендациями Лос-Аламосской лаборатории. В вычислительной газовой динамике «наилучшее» представление конвективных и диффузионных членов является существенным либо для точности и сходимости, либо устойчивости итерационной схемы, либо маршевой процедуры. При больших значениях рассчитанного по размеру ячейки числа Рейнольдса существенным является использование в определенной степени «разностей против потока», например, таких методов, как встречные разности, гибридные схемы, лос-аламосская «молния», схема с донорскими ячейками и т. д. Методы решения также могут широко варьироваться от точечного метода Гаусса — Зайделя до более эффективного построчного метода SIMPLE (полунеявный метод для связанных по давлению уравнений), методов для стационарных задач с соответствующими явными методами или методами типа SIMPLE для решения нестационарных задач [78, 89—92]. Применение методов конечных элементов для задач с горением в случае сложных граничных условий и при сложной конфигурации границ находится в зачаточном состоянии, дальнейшая разработка этого плодотворного направления может оказаться очень полезной [2].

