Введение
Имеется возможность не только использовать эмпирические соотношения, полученные по экспериментальным результатам, но и рассчитать влияние входных параметров на поле скоростей закрученного течения в циклонной камере. Первый подход был популярен несколько лет назад и эффективно использовался, как отмечено ранее в этой главе. Сегодня исследователи подошли к расчету сильнозакрученных течений внутри таких камер с помощью системы дифференциальных уравнений с частными производными, в некоторых случаях с включением в поле течения частиц различных размеров, которые в общем случае могут быть как инертными, так и горящими. Так, с помощью метода, представленного в гл. 2 работы [118], можно непосредственно рассчитать поле течения.
Для сепараторов пыли, топок и ряда высокотемпературных процессов главной является возможность рассчитать влияние конструктивных параметров на аэродинамику течения в циклонной камере. В общем случае эти потоки имеют цилиндрическую конфигурацию выходное отверстие расположено на оси, а входные каналы — по окружности; рабочее тело, поступающее по входным каналам, приобретает в вихревой камере вращательное движение. Входные каналы могут быть расположены вблизи выхода из камеры или на противоположной стороне, а также с обеих сторон. Полезные свойства и основные характеристики процессов, происходящих в циклоне, определяются главным образом конкретной структурой течения в нем, которая зависит от ряда конструктивных параметров, включая диаметр в длину камеры, размер выходного отверстия, размеры и расположение входных каналов, а также скорости и расходы во входных каналах. Целью данного раздела является описание непосредственного расчета течений в циклонах на основе уравнений газовой динамики для случая предполагаемой осевой симметрии потока.
В начале 70-х гг. в работе [119] был выполнен фундаментальный анализ и позже — достаточно успешное прямое численное решение системы уравнений для закрученных потоков, содержащих частицы пыли. Дальнейшие работы были направлены на более адекватное моделирование течения [120]. С математической точки зрения определяющие уравнения являются эллиптическими, и при их решении можно пользоваться методом релаксации (при прямом решении стационарной задачи); если решать стационарную задачу с эволюцией по времени переходных состояний потока, уравнения будут параболическими по времени, поэтому здесь подходит решение методом установленных переменных естественные величины — давление и скорость, а не вводить функцию тока и завихренность, однако последний подход используется, например, при решении задачи о горении угольной пыли в закрученном потоке с внезапным расширением [121]. Ниже обсуждаются два конкретных подхода: первый представляет простую явную схему решения задачи методом установления по времени, а второй, более сложный,— процедуру решения стационарной задачи.
Расчет основных явлений простым методом.
В последнее время разработана процедура расчета осесимметричного закрученного течения в циклонных камерах [122].

На основе идей, заложенных в программе двумерного расчета SOLA, разработанной в исследовательском центре Лос-Аламоса [123], решаются нестационарные уравнения Навье — Стокса для несжимаемой жидкости с помощью соответствующих конечно-разностных уравнений, составленных в естественных переменных давление — скорость. Метод упрощен для облегчения его использования теми, кто имеет лишь небольшой опыт в области расчетной газовой динамики; например, предельно просто задаются граничные условия. Алгоритм программы представляет собой, таким образом, основной инструмент, к которому пользователь может легко добавить требуемые усложнения и особенности.
Представленные результаты и их обсуждение особенно полезны конструкторам циклонных камер, предназначенных для сжигания топлива.
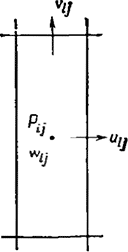
Рис. 5.316 Расположение переменных конечно-разностного уравнения в типичной ячейке [122].
Используются конечно-разностные уравнения Эйлера, в которых основными зависимыми переменным» являются давление и скорость. Значения компонент скорости располагаются между узлами сетки, а в узлах — значения давления и других переменных. На каждом шаге по времени величины и, v и w для последующего шага подставляются в уравнение неразрывности, выраженное в конечно-разностной форме для каждой ячейки, и итерационный процесс задания и коррекции давления и коррекция скорости повторяются до тех пор, пока не будет с достаточной точностью удовлетворяться уравнение неразрывности. В работе [118] содержится подробное обсуждение уравнения, расчетной сетки, дифференцирования навстречу потоку и ввода граничных условий.
На рис. 5.31а показано разбиение цилиндрической области на прямоугольные ячейки равного размера. Эта расчетная область дополнена слоем ячеек со всех сторон, так чтобы было легко ввести требуемые граничные условия. На рис. 5.31б приведены одна увеличенная ячейка сетки и расположение каждой переменной поля р, и, υ и w относительно этой ячейки. Значения давления и окружной скорости w расположены в центре каждой ячейки, а значения радиальной и осевой скоростей находятся соответственно на правой и верхней границах. Таким образом, нормальные скорости лежат на физических границах области решения, а окружная скорость и давление смешены на половину ячейки внутрь поля течения. В этом случае использование внешних фиктивных ячеек особенно удобно для постановки граничных условий.
Для демонстрации возможностей этой схемы решения вы полнены расчеты небольшой циклонной камеры, которая подобна камере, исследованной ранее экспериментально [124]; ниже обсуждаются результаты расчетов. В работе [122] описаны три следующие группы расчетов: 1) закручивающий боковой входной канал расположен с противоположной стороны от круглого выходного отверстия (нижний подвод), что показано на рис. 5.32: 2) входной канал расположен (рис 5.33) с той же стороны, что и выход (верхний подвод); 3) входные каналы расположены с обеих сторон (верхний и нижний подводы).
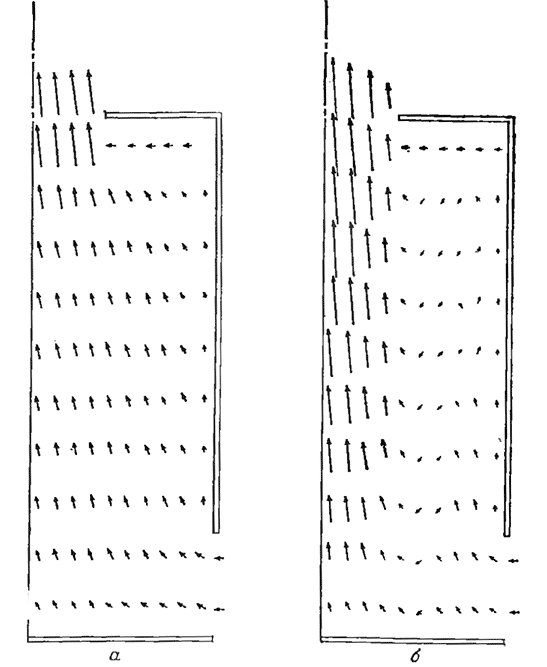
Рис. 5.32. Результаты расчета поля векторов скорости в циклонной камере с нижним подводом при слабой и сильной закрутке [122]
a — SR= 0,1; б-SR= 10.
Вначале были выполнены расчеты циклонной камеры с нижним подводом. Обычно циклонная камера разбивалась по осям х и у на ячейки сеткой 20 X 20, а размеры ячейки составляли соответственно 0,00625 и 0,0175 м. При кольцевом входе высотой 0,06 м и радиальной входной скорости 0,1 м/с средняя скорость в камере 0,112 м/с и средняя скорость в расположенном сверху круглом выходном отверстии, имеющем радиус 0,05 м, равна 0,7 м/с.
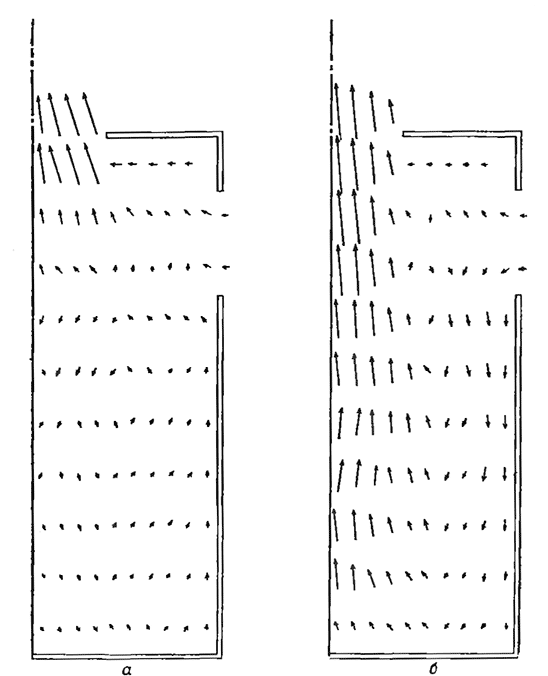
Рис 5.33. Результаты расчета поля векторов скорости в циклонной камере с верхним подводом при слабой н сильной закрутке [122]: a-SR = 0,1; б - SR = 10.
Расчеты нестационарного состояния продолжались до самостоятельного установления стационарного состояния; это происходило за время, приближенно соответствующее или в два раза большее времени пребывания в камере. Скорости нормировались по средней скорости в камере:
![]()
которая хорошо описывает систему и не зависит от конкретной скорости на входе и площади входа.
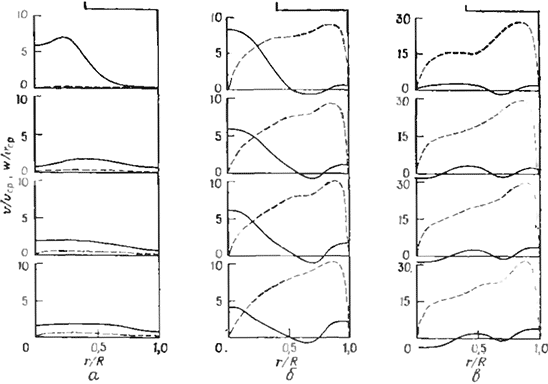
Рис. 5.34. Результаты расчетов профилей приведенных осевой и окружной скоростей v/vcp (сплошные кривые) и w/vср (штриховые кривые) в циклонной κι мере с нижним подводом для трех значений параметра закрутки [122]: и — SR = 0,1: б — SR = 10; в — SR = 30.
Закрутка на входе для данного диаметра камеры лучше всего описывается параметром интенсивности закрутки.
Рассмотрим основные тенденции, которые выявлены в paсчете для заданных интенсивностей закрутки и расположений входных каналов; результаты приведены в виде линий тока плоскости, проходящей через ось симметрии.
На рис. 5.32 показаны результаты предварительных расчетов линий тока в плоскости rх осесимметричной циклонной кг меры, входные каналы которой расположены вблизи основания, а выход по оси верхней стенки. При значении SR = 0, осевое рециркуляционное течение отсутствует, а при SR = 1 вблизи оси в нижней половине камеры возникает рециркуляция в осевом направлении. В последнем случае сильные центробежные эффекты ограничивают проникновение потока и входных каналов к центру, а вблизи наружной стенки образуется восходящий поток.
Результаты соответствующих расчетов для случая, когда входные каналы расположены вблизи верхней стенки, показаны на рис. 5.33. При SR = 0,1 поступающий поток проникает д центральной оси, а поток выше и ниже застойной точки направляется соответственно прямо вверх к выходу и вниз к нижней стенке. В последнем случае формируется восходящий поток наружной стенки и устанавливается зона рециркуляции с вращением против часовой стрелки, как это показано на рис. 5.33. При SR = 10 большие центробежные силы удерживают входящий поток вблизи боковой стенки, и около нее формируется нисходящий поток. Из-за ослабления закрутки вблизи основания возникают движение среды в направлении к оси и восходящее течение прямо в выходное отверстие. Здесь устанавливается рециркуляция по часовой стрелке в противоположность рециркуляции против часовой стрелки, наблюдаемой при меньших значениях SR.
На рис. 5.34 показаны расчетные профили осевой и и окружной w скоростей в четырех сечениях для камеры с нижним подводом при трех значениях параметра закрутки потока на входе, равных SR = 0,1; 10 и 30 (рис. 5.34, соответственно а, б и в). Распределение окружной скорости w описывается известным профилем Рэнкина для свободного вихря, в котором точка максимальной скорости располагается очень близко к боковой стенке. С другой стороны, распределение осевой скорости описывается скругленным профилем с максимумом в центральной части. При низкой интенсивности закрутки (рис. 5.34, а, SR — 0,1), судя по профилям, осевой рециркуляции в камере не существует. Отсутствие воздействия центробежных сил позволяет входящему потоку проникнуть прямо к оси камеры в противоположность случаям более сильной закрутки, когда преобладает действие центробежных сил и поток «прилипает» к боковым стенкам камеры. При более сильной закрутке (рис. 5.34,б, SR = 10) в камере появляется зона рециркуляции с нисходящим потоком, расположенным ближе к стенке, чем к оси камеры симметрии. При наибольшей интенсивности закрутки (рис. 5.34, в, SR = 30) образуется другая зона рециркуляции с нисходящим потоком у оси симметрии; это явление подтверждено экспериментом [73, 124] и расчетами по более сложной методике [125].

