Закрученные потоки - Расчет слабозакрученных течений

Закрученные струи.

Значительный интерес представляют теоретические расчеты турбулентных закрученных течений, и к уравнениям, описывающим слабозакрученные течения и представляющим собой параболические уравнения пограничного слоя, можно применять быстрые методы прямого маршевого интегрирования, обсуждавшиеся в разд. 3.4 [32]. Поэтому они являются удобными испытательными объектами для разработки усовершенствованных моделей турбулентности, которые в дальнейшем будут использоваться в более близких к практике условиях. В 1950— 1960 гг. обычно использовались интегральные автомодельные подходы [15, 20, 23—27, 107, 108], и только в работах [15,17, 27] особо проанализированы турбулентные течения. Хорошее описание такого метода приведено в работе [12] (см. гл. 4), в то время как в работе [13] (см. гл. 5) внимание сосредоточено на иерархии моделей турбулентности, предложенных н применяемых в таких течениях Продемонстрировано хорошее согласие [12, 13, 20] между обширными экспериментальными данными и теоретическими выводами по ключевым параметрам развития турбулентных закрученных струй Кu, Κ1, Кр, Κι и α, обсуждавшихся в разд. 3.1.
С 1970 г. очень популярными стали прямые численные конечно-разностные методы прямого маршевого решения уравнений типа пограничного слоя. Вследствие эффективности и экономичности стала популярной программа GENMIX, разработанная в Имперском колледже и обсуждавшаяся в разд. 3.4.

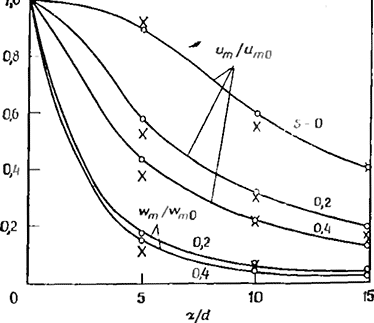
Рис. 3.37. Результаты расчета изменения продольного затухания осевой скорости при увеличении закрутки для инертных закрученных струй. Крестиками отмечены экспериментальные результаты, кружками — расчетные точки.

 Имеются модификации для слабозакрученных течений |[90, 97, 99] с более реалистическим описанием турбулентности, чем с помощью стандартной модели пути смешения Прандтля в исходной программе.
В качестве примера возможности расчета свободной закрученной турбулентной струи могут быть приведены результаты расчета [97] с использованием как модели пути смешения Прандтля, так и модели с уравнениями для энергии и масштаба. Для изотермических закрученных течений были апробированы усовершенствования введением коэффициентов К = 0,6 для модели пути смешения Прандтля и СR = 0,06 для модели с уравнениями для энергии и масштаба (к — Z) вместе с уравнением
где С принимает значения в диапазоне от 2 до 5. (Полное описание модели турбулентности, в которую входят эти параметры, можно найти в разд. 3.4 работы [32].) Расчеты с использованием одной нз моделей дают затухание скорости в продольном направлении для различной интенсивности закрутки, показанное на рис. 3.37. Чтобы провести эти расчеты для изотермических течений, необходимо одновременно решать параболические уравнения в частных производных для и, rw, к и Z. Для упомянутого расчета в приближении пограничного слоя переменная Z берется в виде Z = kl. Скорость вырождения ит и wm хорошо совпадает с экспериментальными данными [20]: очевидны увеличение скорости вырождения ит при увеличении S и сохранение примерно такой же зависимости wm  от продольной координаты, как в незакрученном течении.
Эти и другие результаты показывают, что влияние закрутки на смешение струи может быть должным образом рассчитано с использованием двух моделей турбулентности. Соответственно в работе |97| приведены рекомендации по выбору констант и функций, входящих в эти модели. На практике закрутка струи используется в первую очередь для увеличения угла расширения и темпа вырождения осевой скорости; полем окружной скорости обычно интересуются не в такой степени, как влиянием исходной степени закрутки на последующее течение; например, струя при S = 0,4 почти вдвое шире, чем незакрученная. Это представляет большой интерес для технических приложений, поскольку здесь необходимо знать изменение постоянных, описывающих развитие струн, при увеличении закрутки. Экспериментаторы определили четыре такие постоянные, являющиеся параметрами кривой функции ошибок для осевой скорости (Ки) и закономерностей для описания темпа вырождения осевой скорости (К1), захвата окружающего газа струей (Ке) и полуугла струи (α). Они определяются следующим образом;

Эти выражения обсуждались в разд. 3.1 и здесь приводятся для удобства.

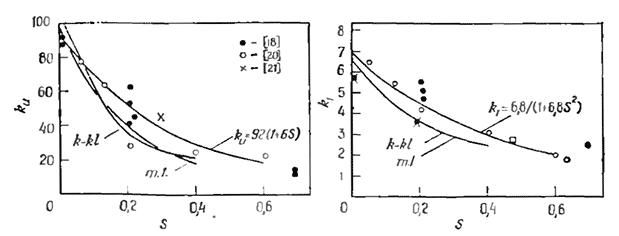
Рис. 3.38. Изменение константы кривой ошибок k для осевой скорости в зависимости от параметра закрутки.
Рис. 3.39. Изменение константы в соотношении для затухания осевой скорости в зависимости от параметра закрутки [97].

Рис. 3.40. Изменение константы в соотношении для захвата массы в зависимости от параметра закрутки [97].

Рис. 3.41. Изменение полуугла расширения струи (0,5) в зависимости от парметра закрутки [97].

Теперь рассмотрим рассчитанные профили. Профиль и изменяется от почти равномерного распределения в начальном сечении к гауссовому в области полностью развитого течения на расстоянии нескольких диаметров вниз по потоку. Профиль w изменяется от распределения, близкого к распределению по закону вращения как целого, к профилю типа распределения в свободном вихре Рэнкина. Для сравнения полученного в результате расчета влияния закрутки на течение вышеупомянутые четыре постоянные были оценены по двум сериям расчетов в области полностью развитого течения при трех значениях параметра закрутки S = 0, 0,2 и 0,4. На рис. 3.38—3.41 результаты расчетов сравниваются с экспериментальными данными. Здесь же приведены рекомендуемые в работе [20] кривые изменения параметров для слабой и умеренной закрутки (как ранее указывалось в разд. 3.1):
Как видно из рисунков, согласие получается вполне удовлетворительное. На рисунках приведены также другие экспериментальные данные, из которых видно, что влияние закрутки на расширение струи, захват воздуха струей из окружающего пространства и затухание скорости в ней можно достаточно точно рассчитать с использованием любой из моделей турбулентности, когда в них внесены соответствующие изменения, позволяющие учесть влияние закрутки.
В других работах для расчета слабозакрученных течений использовались прямые маршевые методы [100], итеративные подходы с переменными ψ — ω [105] и итеративные подходы в переменных p — u — v [83, 109].

Эти и другие работы обсуждаются в разд. 4.8 в связи с сильнозакрученными струями, которые могут содержать рециркуляционные зоны, обусловленные также и геометрическими особенностями течения.
В работах [90, 110, 111] опробованы усовершенствованные методы замыкания с уравнениями второго порядка для напряжений Рейнольдса; результаты их применения обсуждаются в свете подробных измерений напряжений трения в слабозакрученной струе. Утверждается, что в подробном моделировании турбулентности все еще имеется много недостатков, включая невозможность адекватного моделирования rх- и rθ-компонент напряжения. В результате темп затухания скорости в струе и интенсивность ее расширения рассчитываются с большим разбросом [111].

Закрученные пламена

Были рассмотрены также течения с химическими реакциями. В работе [42] обсуждается длина турбулентных закрученных пламен в свободной окружающей среде. В работе [41] представлен подробный перечень параметров, связанных с описанием частично перемешанных пламен с богатой смесью и со слабой закруткой, как изложено в разд 3.2. Экспериментальные данные сопровождаются интегральным анализом с использованием теории подобия [41, 43], дающим хорошее описание. Совсем недавно стали популярными методы прямого численного решения с использованием процедуры прямого маршевого расчета Программа GENMIX, разработанная в Имперском колледже и обсуждавшаяся в разд. 3.4 работы [32], теперь содержит элементы моделирования простой одноступенчатой трехкомпонентной химической реакции предварительно перемешанной смеси; идейная основа этой программы приведена в гл. 2 работы [32].
Имеются решения для таких слабозакрученных пламен в приближении пограничного слоя [112]. Результаты получены путем решения восьми параболических дифференциальных уравнений в частных производных для и, rw, k, kl, h, mfu, max — smfu и др. Расчет проведен для случая предварительно перемешанных пламен (тfи = 0,245), и исходное отношение топливо/воздух было далеко за пределами воспламеняемости. Скорости и градиенты скорости были слишком велики, чтобы пламя могло стабилизироваться на кромках горелки, и лишь на расстоянии 4—6 диаметров вниз по потоку они уменьшались настолько, чтобы мог образоваться кольцевой фронт пламени на границе струи. Основная зона реакции была ограничена кольцевым пространством между холодным центральным ядром и холодным окружающим воздухом, температуры в ядре возрастали вниз по потоку в основном в результате турбулентного смешения с горячими продуктами сгорания из зоны реакции.

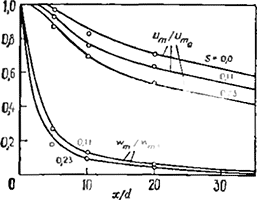
Рис. 3.42. Продольное затухание скорости при расчете с использованием k — kl-модели (кружками отмечены экспериментальные данные) [112].

Рис. 3.43. Продольное изменение величии Тс и mfu, полученное в расчете с использованием k— kl модели (крестиками отмечены экспериментальные данные) [112].

Расчет начинался в выходном сечении горелки с холодной предварительно перемешанной начальной части струн. Скорости истечения менялись в пределах 60 ... 100 м/с, и химическая реакция могла начаться только там, где позволял уровень скорости и градиента скорости [41]. Были рассмотрены модель пути смешения Прандтля и модель турбулентности с уравнениями для к и kl с введенной анизотропией, но представлены результаты только с использованием модели с отрывом вихрей. Модель химической реакции обсуждается более подробно в гл. 2 работы [32] со значениями постоянных Сeви, Cg1 и Cg2, равными соответственно 0,53, 3,0 и 1,32. Расчеты со значением параметра в модели пути смешения Прандтля λs=1,2 и параметра в модели с уравнениями для к и kl Cr = 0,15 вместе с определенной степенью анизотропии σrθ = 1+5S дают затухание иm и wm в продольном направлении, хорошо совпадающее с экспериментальными данными, как показано на рис. 3.42 для двухпараметрической модели турбулентности. Темп затухания хорошо совпадает с экспериментальными данными, и видно постепенное увеличение темпа затухания ит и wm с увеличением S. Следует отметить, что темп затухания скорости меньше, чем в холодных закрученных струях. Это объясняется главным образом изменениями температуры н плотности. В результате расширения газа возрастают осевая и радиальная скорости, что дает уменьшение темпа затухания ит и большую ширину струн на начальном участке.

Рис. 3.44. Полеченные в результате расчета контуры фронта пламени для слабозакрученных струйных пламен [112].

На рис. 3.43 представлено продольное изменение температуры на оси Тс и общего потока массы несгоревшего горючего при различной закрутке. Заметим, что Тс возрастает быстрее при увеличении S, что указывает на более быстрое смешение горячих продуктов сгорания с более холодным газом из высокоскоростной области ядра. Заметим также, что mfu с возрастанием S уменьшается быстрее, что указывает на более быстрое потребление топлива на единицу длины пламени. Расчеты поля температуры проясняют влияние закрутки на размер пламени, его форму и интенсивность сгорания. На рис. 3.44 показаны линии фронта пламени (геометрическое место точек максимумов температуры), и видно, что длина пламени заметно уменьшается при увеличении закрутки и что наблюдается постепенное увеличение начальной ширины (при x/d = 10) пламени при увеличении закрутки. Как видно из табл. 3.3, длины пламени, определенные по рис. 3.44, хорошо согласуются с экспериментальными данными.

Таблица 3.3. Длина пламени.

Приведенные результаты показывают, что влияние закрутки на развитие струйного пламени может быть рассчитано с использованием любой нз двух моделей турбулентности, если в них внесены соответствующие изменения. Основной эффект закрутки в струйном пламени состоит в увеличении ширины пламени и интенсивности захвата массы, ускорении затухания осевой скорости и уменьшении длины пламени. Поле окружной скорости имеет второстепенное значение для влияния исходной степени закрутки на последующее течение. Это представляет значительный интерес для технических приложений, и для практических целей необходимо знать изменение параметров, описывающих развитие пламени при введении закрутки, что· обсуждалось в разд. 3.2. С точки зрения практических применений рассчитанные параметры достаточно хорошо совпадают с экспериментальными значениями [112].
Тем не менее, становится все очевиднее, что последовательный вывод соответствующих уравнений для осесимметричного закрученного потока с замыканием для напряжений Рейнольдса второго порядка, по Лаундеру и др. [89], не позволяет провести хороший расчет [III] общих черт слабозакрученной струи, описанных в работе [21]. Рассчитанные значения компоненты напряжения u'w' фактически имеют противоположный знак по сравнению с экспериментальными значениями во многих точках, и скорость смешения уменьшается при увеличении интенсивности закрутки, что противоположно наблюдаемому в. эксперименте увеличению. Вероятно, необходимо использовать более совершенные модели [113]. В работе [114] анализ слабозакрученных течений проведен с использованием криволинейных, подобранных применительно к форме тела координат, и модели турбулентности Саффмана — Уилкокса [115— 117] для напряжений Рейнольдса. И наконец, дальнейшие разработки методов расчета слабозакрученных течений с использованием итеративных подходов в переменных φ— ω и р — и—и обсуждаются подробно в следующей главе применительно к ограниченным течениям с обратными потоками, частично связанными с их геометрическими особенностями.