Г лава I
Введение
ХАРАКТЕРИСТИКИ ЗАКРУЧЕННЫХ ПОТОКОВ
Сильное влияние закрутки на инертные и реагирующие течения хорошо известно и изучается на протяжении многих лет. Когда эффект закрутки оказывается полезным, конструктор старается создать закрутку, наиболее подходящую для решения его задач; если же подобные эффекты нежелательны, конструктор предпринимает усилия для регулирования или устранения закрутки. Данная книга задумана как всестороннее и иллюстрированное введение в совокупность проблем, связанных с явлением закрутки, при ее возникновении в атмосфере и в технических устройствах с горением и без горения. Закрученные течения имеют широкий диапазон приложений. В случае отсутствия химических реакций сюда относятся, например, течения в вихревых реакторах, циклонных сепараторах и трубах Ранка — Хилша, при срыве вихревой пелены с крыльев самолета, в водоворотах и торнадо, в устройствах для распыления аэрозолей в сельском хозяйстве, в теплообменниках, струпных насосах, а также теория бумеранга и полета пчелы. В течениях с горением широко используется сильное благоприятное влияние закрутки инжектируемых воздуха и горючего на улучшение стабилизации высокоинтенсивных процессов горения и при организации эффективного чистого сгорания во многих практических устройствах; в бензиновых и дизельных двигателях, в газовых турбинах, промышленных печах, бойлерах и других технических нагревательных аппаратах. В последнее время усилия исследователей были направлены на понимание в описание аэродинамики закрученных течений с процессами горения газообразных, жидких и твердых топлив. Экономичное конструирование и экологичность работы технических устройств с горением могут быть значительно улучшены дополнительными экспериментами и модельными исследованиями. При том экспериментальная, теоретическая аэродинамика течений с горением используется вместе со сложными методами вычислительной гидродинамики. Развитие и совершенствование этих методов позволят значительно снизить затраты времени, средств на программы развития новых устройств. Подробные обзоры этих исследований можно найти в литературе [1—15].
Закрученные течения являются результатом сообщения потоку спирального движения с помощью закручивающих лопаток, при использовании генераторов закрутки с осевым и тангенциальным подводом или прямой закруткой путем тангенциальной подачи в камеру с формированием окружной компоненты скорости (называемой также тангенциальной или азимутальной компонентой скорости). Экспериментальные исследования показывают, что закрутка оказывает крупномасштабное влияние на поле течения: на расширение струи, процессы подмешивания и затухания скорости в струе (в случае инертных струй), на размеры, форму и устойчивость пламени и интенсивность горения (в случае реагирующих потоков). На все эти характеристики влияет интенсивность закрутки потока. Интенсивность закрутки обычно характеризуется параметром закрутки, представляющим собой безразмерное отношение осевой компоненты потока момента количества движения к произведению осевой компоненты потока количества движения и эквивалентного радиуса сопла, т. е.
![]() (1.1)
(1.1)
где величина
![]() (1.2)
(1.2)
является потоком момента количества движения в осевом направлении и учитывает вклад х—θ-компоненты турбулентного сдвигового напряжения; величина
![]() (1.3)
(1.3)
является потоком количества движения в осевом направлении и учитывает вклад турбулентного нормального напряжения и давления (осевая тяга), d/2— радиус сопла, и, v, w — компоненты скорости в направлении осей х, r, θ цилиндрической системы координат.
В свободной струе, распространяющейся в затопленном пространстве, величины G0, Gx постоянны, т. е. являются инвариантами для данной струн.
Если использовать уравнение для количества движения в радиальном направлении и пренебречь слагаемым и' — (w'2 + v'2)/2, то вклад давления в Gх можно выразить через ω следующим образом: ![]()
Эту характеристику зачастую трудно измерить с хорошей точностью, поэтому используются альтернативные упрощенные варианты. Иногда величину S рассчитывают без учета турбулентных напряжений, иногда пренебрегают вкладом давления. В этих случаях величины Gθ и Gx при смещении вниз по потоку не сохраняются.
(1.5)

Рис. 1.1. Соотношение между параметрами
S и G, характеризующими закрутку (16).
Связь S и G проиллюстрирована на рис. 1.1, где также приведены экспериментальные значения [16] измеренных независимо величин S и G. Соотношение S ~ G для вращения газа как целого правдоподобно описывает реальный случай истечения из генератора закрутки при G < 0,4 (S ≈ 0,2). Однако при более высокой интенсивности закрутки распределение осевой скорости значительно отклоняется от равномерного; большая часть потока выходит из отверстия вблизи внешней кромки; в качестве примера на рис. 1.2 приведены распределения осевой, окружной и радиальной скоростей в кольцевом выходном сечении генератора закрутки с тангенциальным и осевым подводом, полученные экспериментально при нескольких значениях параметра закрутки [17].
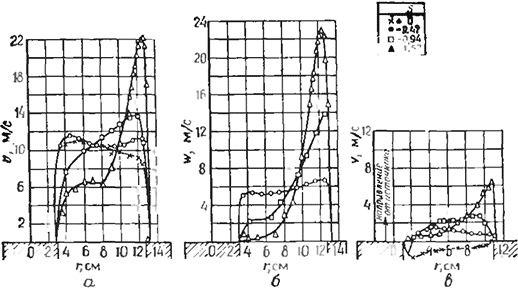
Рис. 1.2. Радиальные распределения осевой, окружной н радиальной скоростей на выходе из закручивающего устройства со смешанной тангенциально-осевой подачей, демонстрирующие влияние изменения степени закрутки (S = Go/Gxr2) (17):
С—осевая скорость; б — окружная скорость: в—радиальная скорость
Указанная теоретическая зависимость
S ~ G дает в этом случае заниженные значения S при заданных значениях G, так что фактически более реальным оказывается следующее соотношение между S и G:
![]() (1.6)
(1.6)
также изображенное на рис. 1.1.
Течение может быть охарактеризовано также локальным параметром закрутки Sx, в котором используется толщина слоя смешения d/2, а не радиус сопла d/2. Кроме того, закрутка потока может выражаться непосредственно через угол установки лопаток закручивающего аппарата и геометрические параметры сопла, через тягу и вращающий момент закручивающего устройства, через угол расширения струи вниз по потоку от сопла и через другие параметры. Целесообразно связать угол установки лопаток закручивающего аппарата с создаваемым им значением параметра закрутки.
В этой связи для сравнения следует заметить, что угол установки лопаток φ и параметр закрутки S связаны приближенным соотношением
![]() (1.7)
(1.7)
где d и dh — соответственно диаметры сопла и втулки закручивающего аппарата. Это соотношение вытекает из предположения о распределении осевой скорости в кольцевом канале, соответствующем движению газа как целого, и допущению о
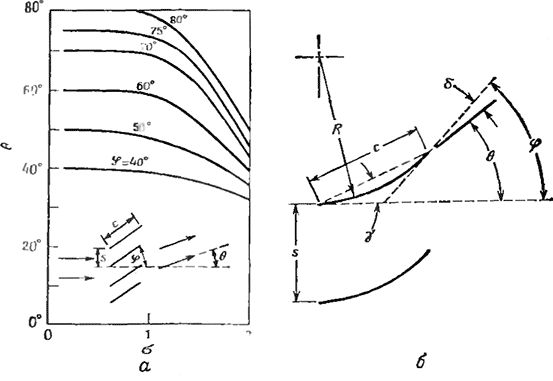
Рис. 1.3. Изменение угла выхода 0 для закручивающего устройства с плоскими лопатками в зависимости от угла установки лопаток φ и отношения шага установки к хорде σ=s/c, полученное на основе данных для каскада плоских лопаток [131 (а) и данных для каскада криволинейных лопате (б).
Действительно, интегрируя выражения (1.2), (1.3) по r от Rh = dh/2 до R = d/2, получим
![]()
малой толщине лопаток, имеющих постоянный угол φ по отношению к направлению основного потока и сообщающих потоку постоянную скорость закрутки.
откуда следует соотношение (1.7).
В случае безвтулочного закручивающего аппарата (или для аппарата с очень малым отношением d/d) приведенное выше выражение упрощается следующим образом:
![]()
(1.8
так что, например, углы установки лопаток 15°, 30, 45o, 60°, 70° и 80o соответствуют значениям S, равным примерно 0,2; 0,4; 0,7; 1,2; 2.0 и 4.0 соответственно. Здесь предполагается 100 %-ная эффективность закручивающего аппарата, но в действительности она уменьшается при увеличении угла установки. На рис. 1.3 приведен примерный вид зависимости угла выхода потока воздуха θ для закручивающего аппарата с плоскими лопатками от угла установки лопаток φ и отношения шага установки лопаток к длине хорды
σ = s/c. Следует также отметить, что целесообразно использовать изогнутые лопатки в решетках закручивающих аппаратов, и по некоторым экспериментальным данным известно, что эффективный угол закрутки, сообщаемой потоку, определяется углом установки задней кромки. На рис. 1.3,б приведены соответствующие обозначения для угла выхода потока воздуха θ, зависящего от угла установки задней кромки лопатки φ (равного 180° — у) и отношения шага установки лопаток к длине хорды σ. Здесь использованы следующие обозначения:
θ — угол поворота потока,
φ — конечный угол поворота лопаток,
δ — угол отставания, равный φ — θ,
γ — угол хорды лопатки, равный 180° — φ,
R — радиус кривизны,
с — длина хорды лопатки,
s — расстояние между лопатками (шаг установки лопаток), и связь между этими параметрами выражается приближенным соотношением Картера
![]()
где Мс — функция угла хорды лопатки, которую можно аппроксимировать выражением
![]()
И наконец, в случае закручивающего устройства с адаптивным блоком (см. разд. 1.2 и гл. 4) параметр закрутки определяется следующим выражением:
![]() (1-9)
(1-9)
где σ = w1/v1 для радиально подводимого потока, R и R и — внешний и внутренний радиусы устройства, В — длина устройства. Формула (1.9) детально обсуждается в гл. 4.
(1.10)
Изучение камер сгорания различных размеров при использовании входных сопел одинакового размера с одинаковым углом установки лопаток φ показало, что размер и форма центральной тороидальной рециркуляционной зоны (ЦТРЗ) зависят от диаметра камеры сгорания [18]. Для описания реализующихся в этом случае типов течений удобно использовать модифицированный параметр закрутки ![]() в котором диаметр сопла заменяется диаметром камеры сгорания.
в котором диаметр сопла заменяется диаметром камеры сгорания.
(Заметим, что в работе 118) величина параметра S определяется с помощью диаметра, а не радиуса камеры сгорания, и поэтому введенная там величина S* = S'/2.)

