Турбулентность представляет собой наиболее часто встречающийся, наиболее важный и наиболее сложный тип движения сплошной среды из числа тех, которые обычно наблюдаются в различного рода практических устройствах с горением. Турбулентное горение интенсивно изучалось в течение длительного периода времени, но общепризнанная теория, которая могла бы с единых позиций удовлетворительно объяснить целый ряд характеристик турбулентных пламен, по-видимому, все еще не создана. Одной из важных причин подобной незавершенности в данной области следует считать недостаточное понимание тех процессов, которые протекают в той зоне пламени, где собственно и происходит горение. Турбулентность представляет собой нерегулярные флуктуации (пульсации) в небольших объемах среды (жидкости, газа), которые накладываются на перемещение этой среды в целом. Турбулентные пульсации происходят случайным образом и имеют определенное сходство с хаотическим движением молекул, но, например, количественные характеристики турбулентности, аналогичные массе молекулы и длине ее свободного пробега, не являются постоянными для данной среды. В то же время, поскольку масса турбулентных объемов и средняя длина их «свободного пробега» намного больше аналогичных величин для случая движения молекул, турбулентный перенос вещества происходит значительно более интенсивно, чем перенос посредством молекулярной диффузии. Применительно к турбулентному горению самой важной особенностью турбулентности следует считать распределение скоростей, которое удобно характеризовать энергетическим спектром турбулентности (рис. 2.6) и масштабом турбулентности [20].
Турбулентные пульсации — это результат образования вихрей в течении со сдвигом, которое формируется на границе двух смешивающихся потоков вязкой жидкости, имеющих разную скорость. Потоки могут представлять собой индивидуальные струи, включая «струи с нулевой скоростью» за торцами обтекаемых потоком тел или пограничные слои на поверхностях обтекаемых тел. В устройствах с горением свободные пограничные слои такого типа (после их отрыва от тела) наиболее важны.
Крупные вихри, формируемые смешивающимися потоками, вначале существенно анизотропны. Эти вихри взаимодействуют в дальнейшем между собой и образуют в результате целый спектр вихрей, характеризуемый определенными частотами (рис. 2.6), и турбулентность становится приблизительно изотропной (т. е. в потоке не существует какого-либо предпочтительного, чем-то отличающегося от других направления). Наименьшие вихри с наибольшими значениями волнового числа k посредством вязких сил диссипируют энергию турбулентности в тепло. Потеря энергии крупными вихрями происходит главным образом вследствие ее передачи к вихрям меньшего размера. Область спектра, отмеченная как равновесный интервал, характеризуется тем, что она не зависит от начальных условий формирования крупных вихрей.
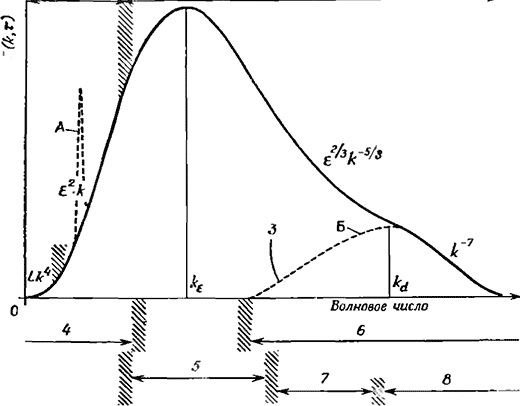
Рис. 2.6- Трехмерный спектр изотропной турбулентности [2]:
1 — область влияния условий образования вихрей; 2 — область отсутствия влияния условий образования вихрей; 3 — спектр диссипации; 4 — наибольшие вихри непрерывного характера; 5 — энергосодержащие вихри; 6 — равновесный интервал; 7 — инерционный интервал; 8 — интервал вязкой диссипации.
Отметим, что этот интервал включает и область диссипации с малыми вихрями, в которой происходит перемешивание вплоть до молекулярного уровня. В устройствах с горением, если только газы не перемешаны до молекулярного уровня заранее, они в сущности и не перемешиваются до такой степени и, следовательно, химические реакции не могут завершиться полностью.
Спектр турбулентности на рис. 2.6 дает представление о средней энергии турбулентного движения, заключенной в вихрях с волновыми числами между k и k + ∆k. Для изотропной турбулентности среднеквадратичные пульсации скорости во всех трех измерениях равны, поэтому полная кинетическая энергия турбулентности на единицу массы равна
(2.20)
и плотность кинетической энергии Ет равна
(2.21)
где u, ν' и w' — пульсационные составляющие соответственно осевой, радиальной и окружной скоростей.
Важной особенностью является то, что суммарная энергия системы должна сохраняться, и величина максимума кинетической энергии турбулентности может быть получена из баланса энергии без привлечения к рассмотрению локальных значений турбулентной вязкости. Корректность выражения (2.20) может быть подтверждена тем фактом, что приблизительно 80 % всей энергии турбулентности содержится в вихрях за пределами низкочастотного диапазона и, таким образом, в распределении энергии доминирует область изотропной турбулентности. Это выражение, в частности, справедливо для области, в которой завершаются процессы смешения и горения, т. е. вне области формирования первичных вихрей. Необходимо также отметить, что при изотропной турбулентности слагаемые 
обращаются в нуль и среднее сдвиговое напряжение турбулентного трения также равно нулю. Нормальное напряжение трения (при i—j) в этом случае равно
Трехмерный спектр турбулентности может быть разделен на несколько характерных областей (рис. 2.6). В полосе наименьших волновых чисел энергия для изотропной турбулентности возрастает пропорционально k4:
(2.22)
В практических устройствах (например, включающих закрученные потоки) данная область не является изотропной. Тем не менее, так как в этой области заключена лишь небольшая часть полной энергии, ошибка получается незначительной, если не считать зоны, непосредственно примыкающей к закручивающему устройству (завихрителю), пластине — стабилизатору или генератору турбулентности (турбулизатору). Единичный крупный вихрь, существующий в циркуляционной зоне закрученного потока, соответствует очень узкой полосе в спектре энергии турбулентности.
Свитеибэнк [21, 22] использовал диссипативные функции изотропной турбулентности для того, чтобы разработать конструктивный подход, в котором микромасштабные пульсации связываются в дальнейшем с энергией, которая в рассматриваемой системе может служить для генерации турбулентности, и с геометрией камеры сгорания. В практических устройствах с горением источником указанной энергии будут потери полного давления на турбулизирующих поток устройствах и элементах конструкции. Существо данного подхода излагается ниже.
Поскольку пульсации скорости и пульсации концентрации диссинируют одновременно (аналогия Рейнольдса), то предполагается, во-первых, что достигаемая степень смешения равна степени диссипации турбулентности в условиях данного течения. Баланс энергии в этом случае выполняется следующим образом [22]:
Математически это соответствует равенству
Рис 2.7 Компоненты баланса анергии в потоке.
(2.23), где q — скоростной напор, равный 1/2ρu2.
Для типичных стабилизаторов пламени (турбулизирующих устройств) члены в уравнении (2.23) представлены на рис. 2 7 в виде графиков функций безразмерного расстояния от стабилизатора.
