Глава 2
Пламена, стабилизированные закруткой потока
СТАБИЛИЗАЦИЯ ПЛАМЕНИ
При стационарном горении пламена распространяются навстречу потоку химически активных реагентов. В камере сгорания пламя считается стабилизированным в некотором диапазоне изменения режимных параметров (таких, как расход топлива, отношение топливо/воздух или степень подогрева), если эти изменения не приводят к погасанию пламени или к его проскоку против потока в камере.
На рис. 2.1 в координатах скорость—концентрация схематически показаны характерные области связанных со стабилизацией режимов для открытых пламен на вертикально расположенных горелках (в окружении неподвижного воздуха), которые исследовались в целом ряде работ [1—9]. Если скорость набегающего на стабилизированное пламя потока топливно-воздушной смеси уменьшить настолько, что скорость распространения пламени в некоторой части выходного сечения устья горелки станет больше скорости потока, происходит проскок пламени внутрь горелки. Это происходит в области режимов, отмеченной на рис. 2.1 как «область проскока». Если же, наоборот, скорость набегающего потока увеличивать до тех пор, пока она не превысит в любой точке скорость распространения пламени, то пламя либо погаснет (в случае, когда условия соответствуют на рис. 2.1 области слева от границы срыва пламени), либо (в случае богатой топливно-воздушной смеси) станет подниматься над горелкой, пока не будет достигнуто новое устойчивое положение в потоке газа над устьем горелки, возможное в результате смешения струи смеси с окружающим воздухом и разбавления ее этим воздухом. Граница оторвавшегося (или, как его еще называют, поднятого) пламени представляет собой (на рис. 2.1) продолжение границы срыва в области концентраций топлива в смеси, превышающей некоторое критическое значение (в точке А). Граница срыва (погасания) пламени в этой области соответствует скорости газа, требуемой для того, чтобы погасить оторвавшееся пламя.
Коль скоро пламя поднялось над устьем горелки, то, чтобы оно вернулось обратно и вновь стабилизировалось на кромках горелки, скорость набегающего потока должна быть снижена до величины, значительно меньшей, чем скорость, при которой произошло отделение пламени от горелки. Между значениями концентрации топлива, соответствующими точкам А и β (на графике рис. 2.1), срыв оторвавшегося пламени достигается при меньшей скорости, чем срыв пламени с кромок горелки. Оторвавшееся пламя такого вида можно получить лишь в том случае, если поджигать смесь на некотором расстоянии выше устья горелки.
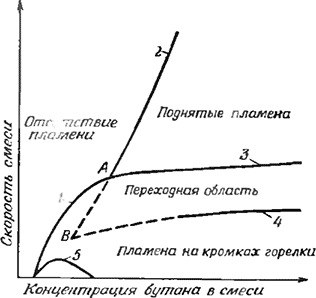
Рис. 2.1. Характеристики стабилизации открытого пламени:
1 — граница срыва пламени; 2 — граница погасания пламени; 3 — граница отрыва пламени от кромок; 4— граница «посадки» пламени на кромки: 5 — область проскока пламени.
Так как массовый расход газа через любое сечение в волне горения постоянный, то плотность р изменяется от ра до рb таким образом, чтобы выполнялось равенство:
Профили температуры и концентрации в одномерном ламинарном пламени показаны на рис. 2.2. Тепло распространяется от продуктов горения, находящихся за граничной поверхностью b, к свежей топливно-воздушной смеси за граничной поверхностью а. Поскольку в направлении оси х происходит расширение газа, то скорость его увеличивается от наименьшего значения Sa на границе а до наибольшего значения Sb на границе b.
(2.1).
В рассматриваемой многокомпонентной смеси перенос каждой компоненты осуществляется не только вместе с общим потоком массы, но также и посредством диффузии, которая происходит в направлении уменьшения концентрации. В итоге молекулы конечных продуктов диффундируют в направлении от b к а, а молекулы реагентов — в направлении от а к b. Скорости диффузии необходимо либо добавлять к скорости потока массы, либо вычитать из нее, так что молекулы реагентов будут, очевидно, перемещаться быстрее, чем молекулы конечных продуктов, и будут до известной степени перемешиваться с ними. Концентрации промежуточных продуктов могут достигать максимума в некотором сечении между границами а и b и они будут дифференцировать отсюда в обоих направлениях.
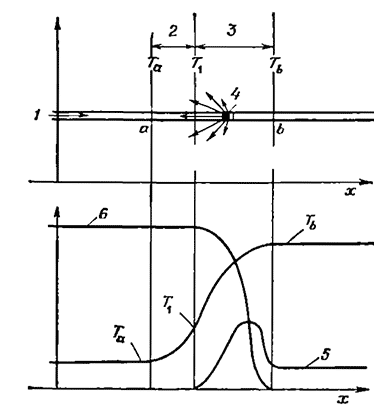
Рис. 2.2. Схематическое представление структуры распространяющейся волны горения [24]:
ί — поток смеси: 2 — зона подогрева; 3 — зона реакции: 4 — поток тепла и активны* центров зарождения цепных реакций от элемента зоны реакции; ΰ — концентрация активных центров: б — концентрация реагентов.
В стационарном режиме горения все эти транспортные процессы происходят таким образом, что суммарная масса вещества, проходящая через поперечное сечение за данный отрезок времени, повсюду одна и та же. Если проследить за прохождением некоторого элемента массы через последовательные стадии в зоне между границами а и b, то окажется, во-первых, что его температура возрастает от величины Та в свежей смеси до величины Т1 в точке перегиба кривой Т=Т(х). Следовательно, в диапазоне температур от Та до Т, вторая производная от температуры d2T/dx2 положительна, и градиент теплового диффузионного потока (d/dx)(kdT/dx), где k—теплопроводность, также будет иметь положительный знак. Это означает, что рассматриваемый элемент массы получает посредством теплопроводности от находящихся ниже по потоку более горячих элементов больше тепла, чем он сам отдает находящимся выше более холодным элементам. После прохождения точки перегиба знак величины d2T/dx2 меняется и она становится отрицательной, в результате чего рассматриваемый элемент перестает быть стоком для тепла и превращается в его источник. Его температура вследствие тепловыделения при химических превращениях продолжает расти. Аналогично можно рассмотреть и изменение концентраций, происходящее в результате диффузии, особенно диффузии промежуточных продуктов, таких, как свободные атомы и радикалы, которые могут служить центрами зарождения цепных химических реакций.
Но при этом, хотя температура элемента монотонно возрастает до тех пор, пока не будет достигнута температура конечных продуктов Тb, концентрация химически активных центров цепных реакций может пройти через свой максимум и понизиться затем между атомами, свободными радикалами и нейтральными молекулами на границе b.
Граничные поверхности а и b в волне горения нельзя считать строго определенными, так как изменение температуры вблизи граничных значений Та и Тb происходит непрерывно. Вместе с тем температура вблизи точек а и b меняется достаточно резко, так что некоторая неопределенность в положении границ а и b существует лишь в относительно узких пределах. Вис волны среда находится либо в состоянии термодинамического равновесия, либо в квазиравновесном состоянии, при котором дальнейшие химические и физические изменения происходят настолько медленно, что в адиабатических условиях градиенты температуры и концентрации практически равны нулю.
В любом сечении волны газ состоит из различных компонентов: молекул реагентов, молекул конечных продуктов и молекул и атомов промежуточных продуктов реакций. Рассмотрим компонент i (i меняется в диапазоне 1 ≤ί≤I, где I — общее количество рассматриваемых компонентов). Каждый компонент перемещается относительно сечения волны со скоростью, которая представляет собой сумму средней скорости потока S и скорости диффузии U компонента i. Скорости диффузии компонентов определяются из закона Фика. Скорость диффузии U, может быть как положительной, так и отрицательной в зависимости от знака градиента концентрации i-ro компонента. Массовая скорость компонента i через единицу поверхности пламени получается из уравнения
где n — плотность компонента i, a mi—молекулярная масса. В соответствии с определением среднемассовой скорости выполняется условие
В объеме dx, заключенном
между сечениями в точках х и x + dx единичной площади, количество частиц компонента i равно ndx. В стационарных условиях эта величина не меняется во времени, так что образование или исчезновение молекул компонента i компенсируется разницей в величинах n(S+U) и ni,(S + U), представляющих собой количество частиц, поступающих в рассматриваемый объем и покидающих его. Единственным процессом, приводящим к образованию или исчезновению молекул, является химическая реакция, поэтому
(2.2)
где Ki — скорость изменения плотности ni в результате химических реакций в тех условиях по температуре, плотности и составу газа, которые существуют в окрестности точки к. Поскольку в ходе химической реакции масса не создается и не исчезает, величина K должна удовлетворять уравнению 
Умножая обе части уравнения (2 2) на mi, суммируя по всем компонентам и учитывая, что
приходим к следующему соотношению:
(2.3)
Интегрируя получаем
(2.4)
где т—массовый расход газа через единицу площади.
Рассмотрим бесконечную поверхность фронта пламени, температура внутри которого распределена в соответствии с общим законом, изображенным на рис. 2.2. Предполагая, что уже установился стационарный режим горения, получаем в результате следующее уравнение сохранения энергии:
Первое слагаемое в уравнении (2.5) характеризует изменение температуры за счет теплопроводности, к— теплопроводность, зависящая от х, поскольку эта величина изменяется в зависимости от температуры и состава газа. Второе слагаемое выражает изменение температуры вследствие конвекции, величина Sα — скорость распространения пламени, рα — плотность, ср — удельная теплоемкость при постоянном давлении, средняя для интервала температур от Та до Т и зависящая от х. Третье слагаемое соответствует изменению температуры в результате протекания химических реакций, Q — тепловой эффект реакции, предполагаемый постоянным, и в — доля реакций от их общего числа, завершившихся к сечению х. Таким образом, ΣQiεi представляет собой суммирование вклада реакций по различным компонентам в общую величину Qε. Наконец, последнее слагаемое описывает изменение температуры в результате радиационного теплообмена, R — лучистый поток тепла в сечении х.
Предполагая потери тепла излучением пренебрежимо малыми, уравнение энергии (2,5) для единицы объема газа можно записать в виде
(2.6)
где Q — скорость выделения тепла в химических реакциях. Предположение о малости потерь тепла на излучение оправдано тем, что по закону излучения (Стефана — Больцмана) они зависят от температуры в четвертой степени, в связи с чем заметно излучающая зона должна быть очень узкой, и, кроме того, ширина зоны горения вообще невелика, а составляющий ее газ диатермичен даже в тех областях спектра, где расположены полосы поглощения для трехтомных газов Н2O и СO2, т. е. излучающая способность этого газа мала.
Уравнения сохранения энергии и химической реакции могут быть решены относительно величины массовой скорости горючей смеси и. следовательно, скорости распространения волны горения после задания соответствующих граничных условий. На «горячей» границе b условия определяются обращением в нуль скорости химической реакции, градиентов температуры и концентрации. На «холодной» границе о должны задаваться некоторые искусственные условия в виде температуры воспламенения или же стабилизации пламени В результате решения рассматриваемой системы дифференциальных уравнений величины массовой скорости горючей смеси получаются как собственные значения, и могут быть вычислены распределения температуры и концентрации в волне горения.
Определенные с помощью уравнения (2 6) зависимости градиента температуры и концентрации в волне от координаты х показаны на рис. 2.2. При малых х соответствующее химической реакции слагаемое Q еще мало, так что величина d2T/dx2 приблизительно пропорциональна dT/dx. Это означает, что и температура, и ее градиент сначала возрастают экспоненциально по мере увеличения х и что рост температуры обусловлен притоком тепла, которое выделяется в химической реакции, происходящей при более высокой температуре. Экспоненциальный рост температуры определяется характером увеличения Q c температурой. По мере возрастания Q величина d2T/dx2 уменьшается и наконец становится отрицательной. Соответственно вначале вогнутая кривая изменения температуры становится выпуклой при более высоком уровне температуры, причем выпуклая часть температурной кривой представляет собой зону наибольшего выделения тепла.
Попытки количественного решения уравнений, описывающих распространение волны горения, начались с простого одномерного стационарного случая. Наиболее ранняя попытка такого рода была предпринята Малляром и Ле Шателье [10]. Они вычислили распределение температуры в волне, аналогичное изображенному на рис. 2.2, и предположили, что ее значение в точке перегиба Т1 определяет температуру воспламенения, ниже которой химическая реакция не идет. Процесс диффузии не учитывался. Уравнение сохранения энергии в сечении х1 , соответствующем температуре Τ1, имеет вид
(2.7)
где величина ср — удельная теплоемкость при постоянном давлении, предполагаемая постоянной. Увеличение температуры от Τ1 до Тb вдоль оси х предполагается приблизительно линейным, так что
(2.8)
где ∆х представляет некоторую не очень строго определенную длину, сравнимую с шириной зоны реакции Выражение для скорости распространения волны горения относительно свежей смеси иногда называют уравнением Малляра и Ле Шателье.
Делались попытки усложнить данный подход, вводя выражения для скорости химической реакции. Тем самым можно было исключить неизвестную длину ∆х, но вместо этого вводится такое же неизвестное или чрезмерно упрощенное выражение для скорости реакции (т. е. ∆х заменяется на произведение скорости распространения пламени Sa на время, необходимое для завершения химической реакции после того, как элемент массы пересечет плоскость х1 [10, II]). В ранних ра ботах решения для стационарного случая получались на основе предполагаемых механизмов реакции, но недостаток данных о химической кинетике не позволял ввести в структуру необходимых предположений реальную кинетику внутри волны горения. В результате эти предположения формулировались таким образом, чтобы соответствовать задаче решения только дифференциального уравнения теплопроводности, поскольку процессы диффузии во внимание не принимались.
В работе Льюиса и Эльбе [12] избежать проблемы одновременного решения дифференциальных уравнений теплопроводности и диффузии удалось в предположении, что повсюду в волне горения сумма тепловой и химической энергии на единицу массы постоянна. При этом температура определяется химическим составом и теплопроводность не входит в явном виде в уравнения Зельдович и Франк-Каменецкий [8] изучали волны горения во влажных смесях окиси углерода с кислородом и воспользовались этим же предположением, хотя и в несколько иной математической интерпретации. Приравнивались к продуктам горения и перенос тепла теплопроводностью от продуктов к свежей смеси Этот альтернативный подход к введению предположения о постоянстве суммы тепловой и химической энергий на единицу массы в равной степени позволяет достичь цели и упростить задачу Он дает приближенное решение уравнения энергии (2.6) в виде [8, 79]:
(2.9)
В ходе протекания реакции в элементарном объеме газа скорость этой реакции и, следовательно, количество генерируемого тепла меняются в зависимости от реакционной способности газовой смеси. В самом начале процесса концентрации реагентов велики, но температура мала. По мере увеличения температуры достигается максимум скорости реакции, после чего скорость снижается из-за уменьшения концентрации реагентов. Это можно проиллюстрировать графиком на рис. 2.3, где приведены данные для объемной скорости тепловыделения в замкнутой системе в зависимости от реакционной способности смеси и температуры смеси.
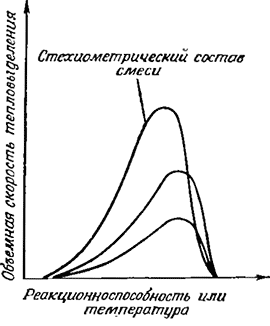
Рис. 2.3. Схематическое представление зависимости скорости тепловыделения в замкнутой системе от реакционной способности смеси или от температуры.
Сильная зависимость скорости распространения от температуры в уравнении (2.9) означает, что и изменения в составе смеси также воздействуют на кривую скорости тепловыделения на рис. 2.3 главным образом вследствие того, что теоретическая температура горения увеличивается по мере того, как величина отношения топливо/воздух приближается к стехиометрическому. Изменения в скорости реакции при варьировании начальной температурой происходят по аналогичной причине.
Для вычисления Q имеющихся данных о кинетике химической реакции недостаточно. Тем не менее, зная общую форму зависимости тепловыделения от температуры и определив среднее значение объемной скорости тепловыделения,
Эджертон и др. [13] предлагают переписать уравнение (2 9) в виде
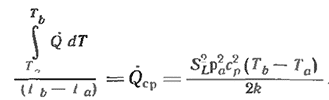(2.10)
Среднее значение объемной скорости тепловыделения Qср можно, таким образом, выразить через поддающиеся измерениям величины и найти его значение, исходя из формы кривой тепловыделения.
