Предыдущее изложение относилось к колебаниям и волнам в макроскопически однородных средах и телах при однородных граничных условиях. Для решения ряда практически важных задач необходимо рассмотрение колебаний систем, в которых неоднородности имеются в объеме или на поверхности. Источниками локальных внутренних неоднородностей могут быть трещины, включения, крупные поры материала, отдельные газовые или паровые пузыри в жидкости. Нелокальные неоднородности могут быть вызваны разностью температуры различных участков, непостоянством химического состава и другими причинами. Поверхностные неоднородности обусловлены шероховатостью поверхности, разной смачиваемостью отдельных участков поверхности, контактом образца материала с волноводами.
Влияние указанных факторов, с одной стороны, нежелательно, поскольку приводит к погрешностям измерений. Однако, с другой стороны, если воздействие контролируемое, то, определяя реакцию на него объекта исследования, можно получить дополнительную информацию о свойствах объекта. Общий метод рассмотрения подобных задач заключается во введении соответствующих слагаемых, зависящих от координат и времени, в уравнения движения и (или) граничные условия. Во многих случаях влияние неоднородностей на намеряемые параметры колебаний сравнительно невелико и эффективно применение метода возмущений, разработанного для исследования и контроля малых образцов материалов резонансным способом [22, 48]. Метод использует математический аппарат теории возмущений и позволяет получить посредством сравнительно несложных расчетов результаты, существенные для исследования реакторных материалов в условиях воздействия высокой температуры и ионизирующих излучений.
Собственные значения связаны с собственными частотами, поэтому по изменению собственных значений легко найти соответствующие им изменения собственных частот. Критерием применения формулы (1.64) является условие Δλ<λ0, позволяющее ограничиться рамками линейной теории возмущений.
Поясним применение метола на примере учета влияния контакта образца в виде тонкой круглой пластинки с волноводом в виде заостренного стержня, с чем обычно приходится сталкиваться при высокотемпературных испытаниях реакторных материалов. Пусть испытании проводятся с использованием нагибных колебаний. Уравнение свободных изгибных колебаний тонкого изотропного однородного диска в цилиндрах.
Нарушение симметрии колебаний образца. Появление даже небольшого возмущения может привести нс только к количественным, но и к качественным изменениям колебаний. В первую очередь это относится к образцам симметричной формы. Если, например, однородный изотропный диск до возмущения не имеет выделенных азимутальных координат и безразлично, от какого его диаметра начинать их отсчет, то при наличии возмущения симметрия нарушается. Это приводит к интересным для практики акустических измерений следствиям. Например, если симметрия свойств образца нарушена из-за наличия в нем небольшого дефекта, в образце появится выделенный азимут и энергия колебаний, а следовательно, и резонансные частоты будут зависеть от взаимной ориентации радиус-векторов, соединяющих центр образца с центром дефекта и точкой возбуждения. Кроме того, возмущение может привести к расщеплению резонансных пиков, когда вместо одной резонансной частоты появляются две, как правило, различающиеся незначительно. Физически это соответствует возможности удовлетворить возмущенным граничным условиям, включая условия на границе внутреннего дефекта, при двух близких значениях частот двумя различными собственными функциями, т. е. двумя модами колебаний, комбинации которых и соответствуют реальные колебания. Математический анализ явления может быть проведен на основе теории групп. Подробный анализ проведен, например, в [46—48], остановимся на его основополагающих моментах и полученных результатах.
Обратимся к общему уравнению невозмущающих колебаний (1.62). В случае колебаний симметричных тел можно получить несколько различных решений ξόη, для которых собственные значения λ0η одинаковы. Например, нетрудно убедиться, что уравнение изгибных колебаний круглой пластины с осесимметричными граничными условиями удовлетворяется двумя линейно независимыми функциями вида
![]()
(1.77а)
(1.77б)
в которых n=0, 1, 2,... — количество узловых диаметров; Rn(r) —функция радиальной координаты, удовлетворяющая граничным условиям, сводящимся в случае колебаний пластин со свободной поверхностью к требованию R(α)=0 (а—радиус пластинки). Функции (1.77а) и (1.77б) равноправны. Нетрудно убедиться непосредственным расчетом, что каждая из них приводит к одним и тем же значениям кинетической и потенциальной энергии колеблющейся пластины, а следовательно, к одному и тому же значению связанной с последними собственной частоты. Подобное явление, когда различным состояниям физической системы соответствует одно и то же значение некоторой физической величины, носит название вырождения, а число различающихся состояний—кратности вырождения данной величины. Поэтому можно сказать, что все собственные частоты изгибных колебаний круглой пластины, кроме частот, соответствующих n=0, двукратно вырождены.
Нарушение симметрии, обусловленное возмущением, приводит к уменьшению кратности вырождения или к полному его исчезновению (снятию вырождения). Следовательно, наличие внутренних неоднородностей в пластине приводит к снятию вырождения собственных частот, что является следствием зависимости энергии колебаний от взаимной ориентации дефекта и упругого поля колебаний, задаваемого источником (возбудителем колебаний). В случае симметричного исходного поля упругих колебаний (n=0) подобная зависимость не имеет места, вырождение отсутствует.
Явление снятия вырождения может быть эффективно использовано для дефектоскопии малых изделий цилиндрической и сферической форм. Увеличение количества резонансных частот по сравнению с эталоном свидетельствует о наличии внутренних дефектов, а величина «расщепления», т. е. разность частот между двумя частотами раздвоившегося резонансного максимума—о степени дефектности [7, 8]. Возможно создание алгоритмов обработки получаемой информации, позволяющих идентифицировать дефекты, определять их местоположение и размеры.
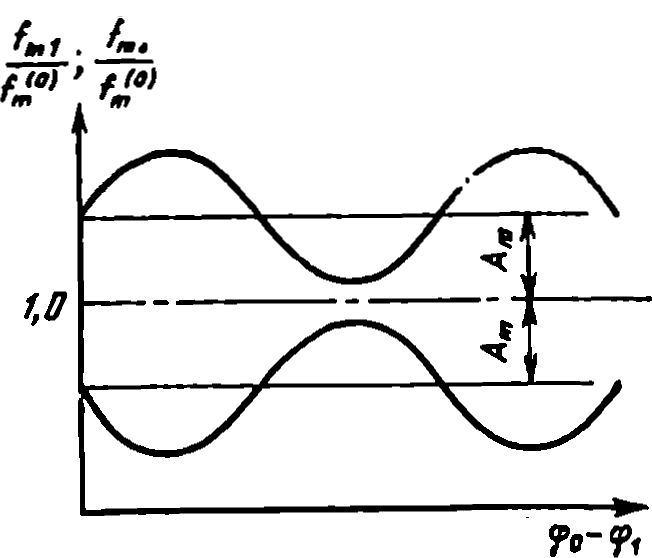
Рис. 1.20. Рассчитанная методом допущений зависимость резонансных частот от ориентации образца в измерительном узле
Если возмущения не являются малыми, требуется строгий рacсчет с видоизмененными уравнениями колебаний или граничными условиями. В любом случае, однако, существует реальная возможность определить характер и размеры неоднородностей объекта исследований по спектру резонансных частот.
В последние годы сходные рассмотренным методы анализа появились и за рубежом,
связи с тем, что резонансные методы позволяют выявить неоднородности материала конструкции, распределенные в пространстве, не обнаруживаемые эхо-методом из-за плавности пространственного изменения акустических характеристик объекта исследования [141]. Для выявления подобных неоднородностей измеряют спектр резонансных частот объекта и сравнивают его со спектром, характеризующим однородный объект. Количественный анализ совокупности отклонений резонансных частот от эталонных позволяет в принципе сколь угодно точно описать имеющуюся неоднородность, однако технические возможности ограничивают практическое применение метода простейшими случаями.
Сущность метода иллюстрируется на примере продольных колебаний топкого длинного стержня со свободными концами (экспериментальная проверка проводилась на медных и алюминиевых проволоках длиной 90 см и диаметром 6 мм).
Предельная пространственная разрешающая способность данного метода зависит от длины волны, соответствующей наивысшей гармонике. Для определения числа резонансных частот N, необходимых для выявления неоднородности с линейным размером вдоль оси стержня, можно воспользоваться соотношением N ≈(0,5-:-0,6). В проведенных экспериментах N≤20, причем выявлялись изменения акустического импеданса менее 3·10-4 распределенные по всей длине стержня (≈90 см).
В случае изменения также и сечения 5 стержня формула (1.83) обобщается:
![]()
где z=ρ0c0S0—волновое сопротивление стержня.
Метод возмущений помимо оценки и исключения систематических погрешностей существенно расширяет возможности акустических измерений, позволяя проводить определение комплекса свойств материалов за один эксперимент. Конкретные возможности и результаты представлены в гл. 5.

