Если поперечные размеры объема среды, в которой распространяется волна (пластина, стержень, труба, заполненная жидкостью или газом) соизмеримы с длиной волны, влияние границ становится существенным. В поперечном направлении образуются стоячие волны, точнее устанавливается определенное распределение смещений по сечению элемента, вдоль которого распространяется волна. При этом возникает геометрическая дисперсия скорости звука, т. е. зависимость скорости упругих воли от частоты, характер которой определяется соотношением между длиной волны и поперечными размерами системы, в которой распространяется волна. Волны, распространяющиеся в телах ограниченных поперечных размеров и характеризующиеся отмеченными особенностями, получили название нормальных. Понятие нормальной волны является развитием понятия нормальных, или собственных, колебаний на случай, когда система не ограничена в одном или двух направлениях, в которых становится возможным распространение бегущих волн.
Соотношения, описывающие зависимость скорости распространения нормальных волн от размеров и свойств среды, а также характер распределения смещений по сечению, следуют из решения волнового уравнения с учетом граничных условий на боковой поверхности, чаще всего требующих исчезновении напряжений (нормальные волны в твердом теле) или смещений (нормальные волны в жидкостях и газах, находящихся в трубах и каналах). Существенно, что распространяющиеся волны в средах с ограниченными поперечными размерами могут представлять только суперпозицию нормальных волн (в простейшем случае—одну нормальную волну). Если условия возбуждения нс способствуют полному превращению энергии колебаний в энергию бегущих нормальных волн, например распределение возбуждающей силы по сечению нс совпадает с распределением колебательных смешений для возможной суперпозиции нормальных волн, часть энергии колебаний расходуется на нераспространяющиеся колебания, локализованные вблизи источника на расстояниях порядка длины волны [66].
Использование нормальных воли в акустической контрольно-измерительной технике, особенно в реакторостроении, трудно переоценить [127). На пх применении основаны чувствительные методы УЗ-контроля оболочек твэлов, топливных сердечников, канальных труб. Общеупотребительна передача акустических сигналов из зоны исследования или контроля элементов ЯЭУ по стержневым звукопроводам.
Свойства и преимущества нормальных воли поясним на примерах, наиболее часто встречающихся в технике—нормальных волнах в пластинах и стержнях.

Рис. 1.10. К определению коэффициентов для расчета затухания волн Лэмба

Рис. 1.11. Основные типы нормальных волк в бесконечных стержнях кругового сечения:
а — растяжения; 6 — изгибные, в — крутильные
Чувствительность волн Лэмба и к продольным дефектам листовых материалов — расслоениям, рискам, выявление которых другими методами часто сопряжено с большими трудностями. Еще одно преимущество контроля с применением волн Лэмба — возможность разнесения излучателя и приемника па расстояние в несколько десятков длин волн, что позволяет выбрать большой шаг сканирования н повысить производительность контроля. Однако контроль обычно осуществляют, погружая изделие в воду, что приводит к возрастанию затухания воли при их распространении из-за излучения энергии в воду. Степень возрастания различна для разных типов волн. Например, для алюминиевой пластины в воде волна S0 при ωh/ct≈4 затухает в е раз на пути около 5 λt, что соответствует 8 мм на частоте 2 МГц при толщине пластины 1 мм. Скорость распространения волны из-за погружения в воду уменьшается на 15%. Для волны βι вблизи критической частоты (c~4ci) затухание в е раз наблюдается на расстоянии около 20 λt, или 3,2 см. В стальной пластине, погруженной в воду, ввиду большей разности удельных волновых сопротивлений стали н воды, чем алюминия и воды, затухание на тех же длинах приблизительно втрое меньше.
Нормальные волны в стержнях кругового сечения.
Стержни небольшого диаметра (I —10 мм) применяют в качестве звукопроводов (волноводов) для передачи акустических сигналов от объекта испытаний и к объекту испытаний, если он находится при высокой температуре, в поле ионизирующих излучений и в других экстремальных условиях. Поэтому рассмотрение характера распространения упругих волн в стержнях представляет особый интерес для акустической контрольно-измерительной техники. Хоти звукопроводы могут быть изогнутыми вследствие действия силы тяжести или по условиям конструкции, обычно радиус кривизны достаточно велик и обусловленные изгибом возмущения невелики. Поэтому будем исходить из результатов, полученных для прямых бесконечных стержней кругового сечения. Наиболее простым является анализ волн в стержне со свободной боковой поверхностью, описывающий работу звукопровода в вакууме или газе (воздухе), когда влиянием упругости внешней среды можно пренебречь. Так же, как и в случае пластин, в стержнях возможно распространение нескольких различных типов волн, характеризующихся различными преобладающими компонентами смещения (рис. 1.11): продольных, крутильных и нагибных.
Рис. 1.13. Зависимость верхней граничной частоты для одномодового волновода продольных волн от коэффициента Пуассона
Для продольной и поперечной компонент смешения соответственно получаются выражения:
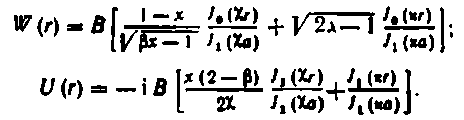
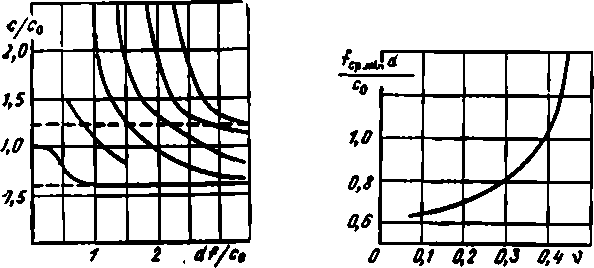
Рис. 1.12. Дисперсионные кривые для продольных волн в бесконечном стержне кругового сечения (v=0,3)
(1.39)
(1.40)
Корни уравнения частот (1.38) дают связь между тремя безразмерными параметрами с/с0, a/λ, v. Уравнение частот при фиксированных значениях v решается численными методами, получаемые дисперсионные кривые выражают зависимость с/с0 от α/λ (где X=c/f). Уравнение имеет кратные корни, и дисперсионные кривые состоит из ряда ветвей, соответствующих основной (низшей) и более высоким формам волн. Вычисление дисперсионных кривых для продольных волн в соответствии с уравнением (1.38) не связано с принципиальными трудностями. На рис. 1.12 приведены дисперсионные кривые для значений коэффициента Пуассона, характерных для некоторых широко применяемых конструкционных материалов; диаметр стержня обозначен d=2α.
Из приведенных зависимостей следует, что в общем случае в цилиндрическом волноводе могут распространяться продольные волны различных типов, характеризующиеся своими значениями фазовых и групповых скоростей, поэтому исходный сигнал дробится на несколько сигналов, число которых в общем случае равно числу распространяющихся воли. Волна каждого типа обладает определенным распределением колебательных смещений по сечению.
Малое значение фазовой скорости нагибных волн на низких частотах обусловливает малое удельное акустическое сопротивление рс. Поэтому изгибно колеблющиеся пластины могут быть лучше согласованы акустически с газообразными средами, вследствие чего они могут быть эффективными излучателями и приемниками акустических волн в воздухе и других газах.
Трансформация волн на концах звукопроводов.
Нормальные волны в твердых звукопроводах рассмотренного типа удовлетворяют граничным условиям отсутствия напряжений только на боковых поверхностях. Например, уже в простейшем случае отражения на свободном конце цилиндрического волновода, когда отражается нормальная продольная волна низшего порядка, граничные условия на конце не выполняются, если отраженная волна является аналогом падающей. Формально этим условиям можно удовлетворить, рассматривая отраженные волны с комплексными волновыми числами, что физически соответствует возникновению экспоненциально затухающих волн вблизи конца волновода, т. с. перераспределению и своеобразной концентрации колебательной энергии вблизи торца. Это явление получило название концевого резонанса и заключается в изменении амплитуды и фазы отраженной нормальной волны.
Поскольку концевые возмущения образуют стоячие волны, они не оказывают влияния на общий баланс энергии, если не учитывается внутреннее трение в материале. При его наличии для поддержания концевых резонансов может потребоваться заметная энергия, что приводит к существенному ослаблению отраженной волны и так называемому радиационному демпфированию [79]. При возможности возникновения нормальных волн высших порядков (высокие частоты колебаний) исчезновение напряжений на конце может обеспечиваться за счет преобразования одних нормальных волн в другие. Соответственно усложняется картина, отражающая совокупность сигналов, обусловленных единичным исходным импульсом. Низшая частота концевого резонанса круглого стержня примерно равна 0,19Ctld (104). Для стального стержня диаметром 3 мм эта частота составляет около 200 кГц.

