Расчетная обеспеченность работы гидроэлектростанции - Аналитический метод построения перспективного графика нагрузки энергосистемы

Таким образом, для построения перспективного графика нагрузки энергосистемы эти методы являются малопригодными, кроме того, с их помощью не представляется возможным произвести обобщения методических построений по исследованию расходной части энергобаланса.
В этом отношении наиболее перспективным является так называемый аналитический метод, сущность которого заключается в представлении действительной кривой изменения нагрузки во времени некоторой аналитической зависимостью. Точность этого метода, разумеется, не может превышать таковую по другим, указанным выше методам. Преимущество же его заключается в простоте расчетных операций и возможности построения на его основе обобщенного приема для анализа расходной части энергобаланса.
Почти все указанные выше авторы для упрощения расчетов и удобства соответствующих анализов преобразуют календарные кривые изменения нагрузки в кривые продолжительности и интегральные. При этом для описания годового графика обычно принимаются среднемесячные нагрузки, что позволяет в значительной мере устранить влияние на него мероприятий по выравниванию суточного графика нагрузки, могущих иметь место при эксплуатации любой энергосистемы.
По данным исследования В. П. Захарова [36], проанализировавшего кривые продолжительности нагрузки различных энергосистем за ряд лет (Мосэнерго, Ленэнерго, Узбекэнерго и др.), из всех эмпирических зависимостей для построения кривой продолжительности нагрузок наиболее удовлетворительный результат дает, формула.
(70)
где Рх — текущее значение нагрузки; Рмакс — абсолютный максимум нагрузки за расчетный период; в — коэффициент пропорциональности;
Тх — время продолжительности текущей величины нагрузки; λ — показатель кривой.

Рис. 21. Кривые продолжительности нагрузки.

Эта формула, по заключению В. П. Захарова, при правильном подборе ее параметров почти на всем протяжении (до 90%) кривой продолжительности дает отклонения не более ±2—3%, т. е. дает довольно высокую достоверность в результате расчета.
При пользовании данной формулой следует различать две части площади графика нагрузки, а именно: основную — прямоугольную, расположенную между осью абсцисс и прямой, параллельной ей, имеющей ординату Р0, соответствующую точке кривой (описываемой этой формулой) при Тх = Т0, и пиковую — криволинейно-очерченную часть кривой, располагающейся выше ординаты Р3 (рис. 21а).

Для определения выработки верхней части графика:
(77)
Значения буквенных обозначений ясны из рисунка 21 б.
Показатель, п является величиной, обратной коэффициенту использования пиковой части графика нагрузки, значение которого
В.  П. Захаров предлагает принимать:
а)  для энергосистемы, в пиковой части графика которой преобладает осветительная нагрузка п = 3,5-4,5;
б)  для случая, когда соотношение между осветительной и моторно-технологической нагрузкой примерно одинаково n= 2,5-3,5;
в)  для случая, когда в пиковой части графика нагрузки преобладает моторная и технологическая нагрузка п = 2,0-:-2,5.
Приведенные выше расчетные соотношения важны для определения значений искомого коэффициента преобразования зарегулированной мощности в рабочую. Однако они для этой цели требуют значительного пересмотра в сторону достижения наибольшей общности расчетного построения и приближения их к решению поставленной нами задачи.
Наибольшая возможность обобщения расчетной методики и приемов анализа обычно появляется при переходе на единые относительные величины. В этом случае отдельные расчетные показатели в известной мере становятся критериями подобия сравниваемых параметров и режимов, что позволяет моделировать изучаемое явление. Поэтому в свете поставленной нами задачи мы полагаем целесообразным все расчетные соотношения построить в относительных величинах.
В качестве базисной величины, относительно которой вычисляются все остальные показатели, нами, принимается максимальная потребная мощность энергосистемы, а в качестве единицы времени продолжительности нагрузки для суточного графика — 24 часа, месячного — 730 часов, а для годового — 8760 часов.

При данной плотности графика нагрузки энергосистемы искомые коэффициенты и характеристики у и хи![. как видно, зависят от показателя кривой продолжительности нагрузки т и удельного веса зарегулированной мощности X0.
Величина показателя т требует дополнительных исследований по фактическим данным графика нагрузки различных энергосистем. К сожалению, почти полное отсутствие опубликованных статистических данных в этом отношении не позволяет привести в настоящей работе величину этого весьма важного показателя. Можно лишь отметить, что величина его, представляемая выражением
(92)
зависит главным образом от коэффициента плотности графика нагрузки системы τн и находится с ним почти в линейной зависимости.
Следует особо оговориться, что в свете рассматриваемых нами вопросов т является показателем кривой продолжительности именно той части графика нагрузки, которая покрывается проектируемой ГЭС. Следовательно, величина т зависит также от ряда эксплуатационных условий, в частности от графика работы параллельно работающих с ГЭС конденсационных тепловых электростанций. При определении значения т это обстоятельство необходимо иметь в виду. В отношении численного значения т для общего графика нагрузки энергосистемы в настоящее время нет никаких опубликованных фактических данных, кроме указанных выше рекомендаций В. П. Захарова.

Ориентируясь в основном на эти указания, полагаем возможным рекомендовать следующие пределы изменения величины т при соответствующих значениях τΗ:

Рис. 22. Изменение коэффициента преобразования зарегулированной мощности ГЭС в располагаемую рабочую (γ) и продолжительности ординат графика нагрузки (tнх) при различных значениях τΗ для т = 0 (1,0 — τΗ).

В целях облегчения труда инженерно-технических работников при массовых предварительных расчетах нами произведено определение величин γ, хг, τнх при всех указанных здесь значениях τ и т, в результате которого построены кривые зависимости γ = f (х0, х и т), xr=f(x0, τн и т) и τнх =f (χ0, хР, т). Эти зависимости, представленные на рисунках 22, 23 и 24, или приведенные выше расчетные формулы (86, 89 и 91) позволяют перейти от зарегулированной мощности (соответствующей обеспеченности) к располагаемой рабочей, участвующей в покрытии максимума графика нагрузки, а также определить продолжительность работы каждой величины этой мощности и удельный вес ее в балансе мощности энергосистемы при заданных значениях ха τн и т. При этом следует отметить, что коэффициент преобразования γ имеет обратную связь с х0 и τ т. е. меньшему значению х0 и τΗ соответствует большее значение γ и, наоборот, большему значению ха и τн— меньшее значение γ.
Величина хг находится в прямой зависимости от х0 и обратной — от τ.
Таким образом, абсолютные значения γ и хг при заданном значении х0 зависят только от плотности графика нагрузки энергосистемы τн и показателя кривой продолжительности нагрузки в пиковой части графика энергопотребления т. Разумеется, это положение справедливо только в том случае, если нет ограничения со стороны других, влияющих на них факторов, а именно — емкости водохранилища, установленной мощности электростанции и эксплуатационных условий.

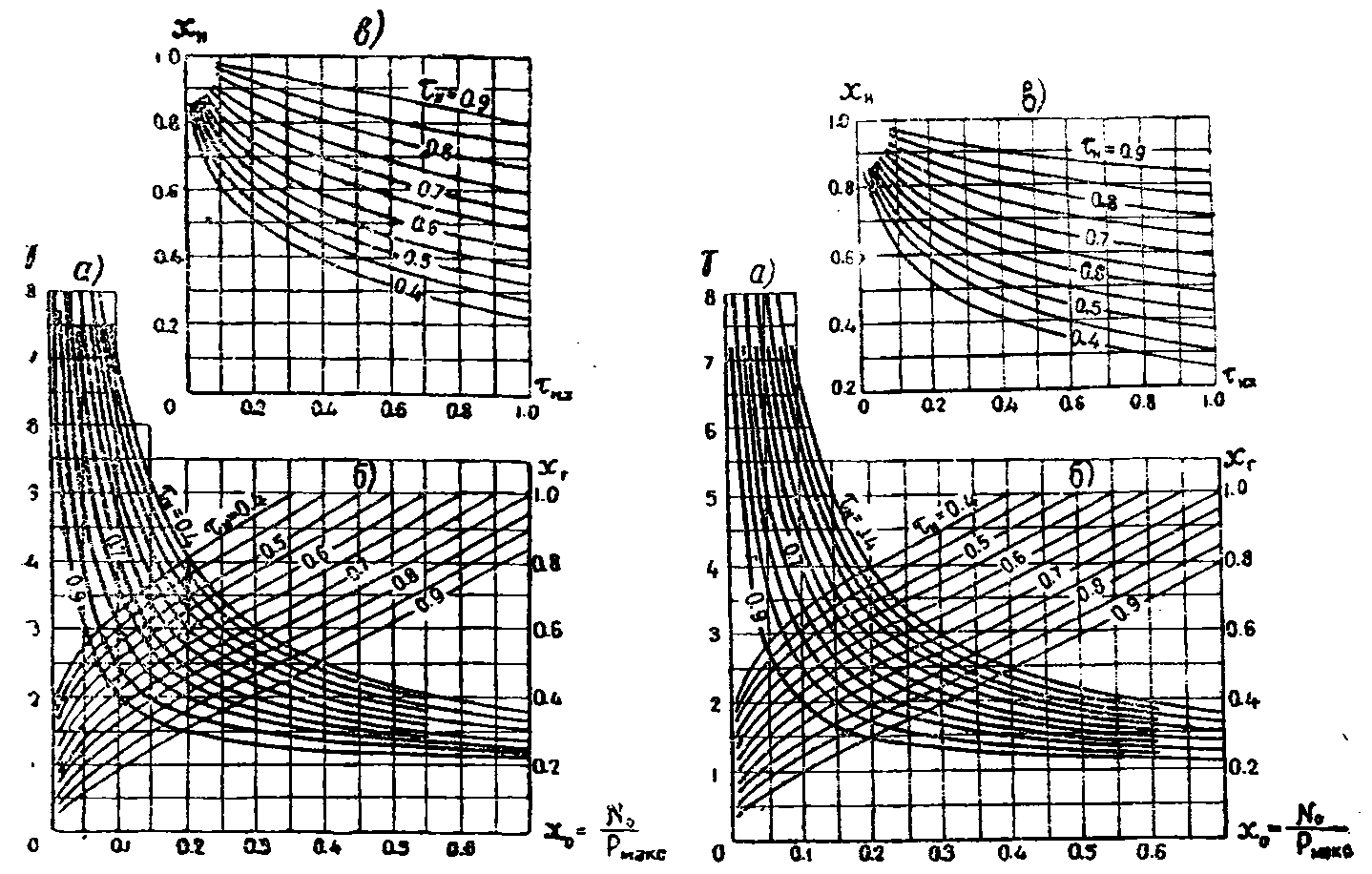
Рис. 23. Изменение коэффициента преобразования зарегулированной мощности ГЭС в располагаемую рабочую ΐγ) и продолжительности ординат графика нагрузки (τΗΧ) при различных значениях тн для т = 5 (1,1 — τн)·

Рис. 24. Изменение коэффициента преобразования зарегулированной мощности ГЭС в располагаемую рабочую (γ) « продолжительности ординат графика нагрузки (тнх) при различных значениях тн для т = 5 (1,2 — τΗ)

Исследование характера влияния последних факторов на закономерности изменения величины γ представляет немалый теоретический и практический интерес. Этот вопрос значительную разработку получил в работах Μ. П. Фельдмана [122, 125], посвященных проблеме установления оптимальной зарегулированности гидроэлектрических станций, в частности вопросу преобразования зарегулированной мощности в располагаемую рабочую.
Автор дает принципиальное расчетное соотношение для определения коэффициента преобразования у:
(93)
В этом уравнении представлены все основные факторы, определяющие величину коэффициента преобразования: характер режима нагрузки, структура генерирующих мощностей системы и показатель предельного использования ТЭС в периоды маловодья.
Абсолютная величина Тт, представляющая режим работы конденсационной тепловой электростанции, зависит от конфигурации графика нагрузки и продолжительности ремонтов и ревизии агрегатов.

Характер нагрузки энергосистемы, представляемый в равенстве через Т, зависит от колебания режима энергопотребления в течение года, месяца, недели и суток.
Анализируя характер изменения каждого из этих факторов и степень влияния их на величину коэффициента преобразования γ, Μ. П. Фельдман дает его изменение в зависимости от удельного значения обеспеченной гидравлической мощности в максимуме нагрузки системы, т. е. оттипа графика энергопотребления Т,
диапазона регулирования и структуры генерирующих мощностей системы. Эти зависимости Μ. П. Фельдмана представлены нами на рисунке 25.

Рис. 25. Изменение коэффициента преобразования зарегулированной мощности ГЭС в рабочую в зависимости от режима нагрузки и диапазона регулирования (по М. II. Фельдману).
При этом для трех типов графиков нагрузки приняты следующие показатели неравномерности:

Здесь— коэффициент полноты суточного графика на
грузки, где Рс — среднесуточная, а Ршкс — максимальная нагрузка системы:
— коэффициент неравномерности недельной нагрузки;
где               Р — средняя недельная нагрузка;
Рс — средняя нагрузка для дня максимального энергопотребления;
Рсез — коэффициент неравномерности сезонной нагрузки при годовом приросте нагрузки в размере 10°/0;
δг — коэффициент полноты годового графика нагрузки Г = δΓ· 8760 = δс-ри-рсез-8760.
Таблица 8

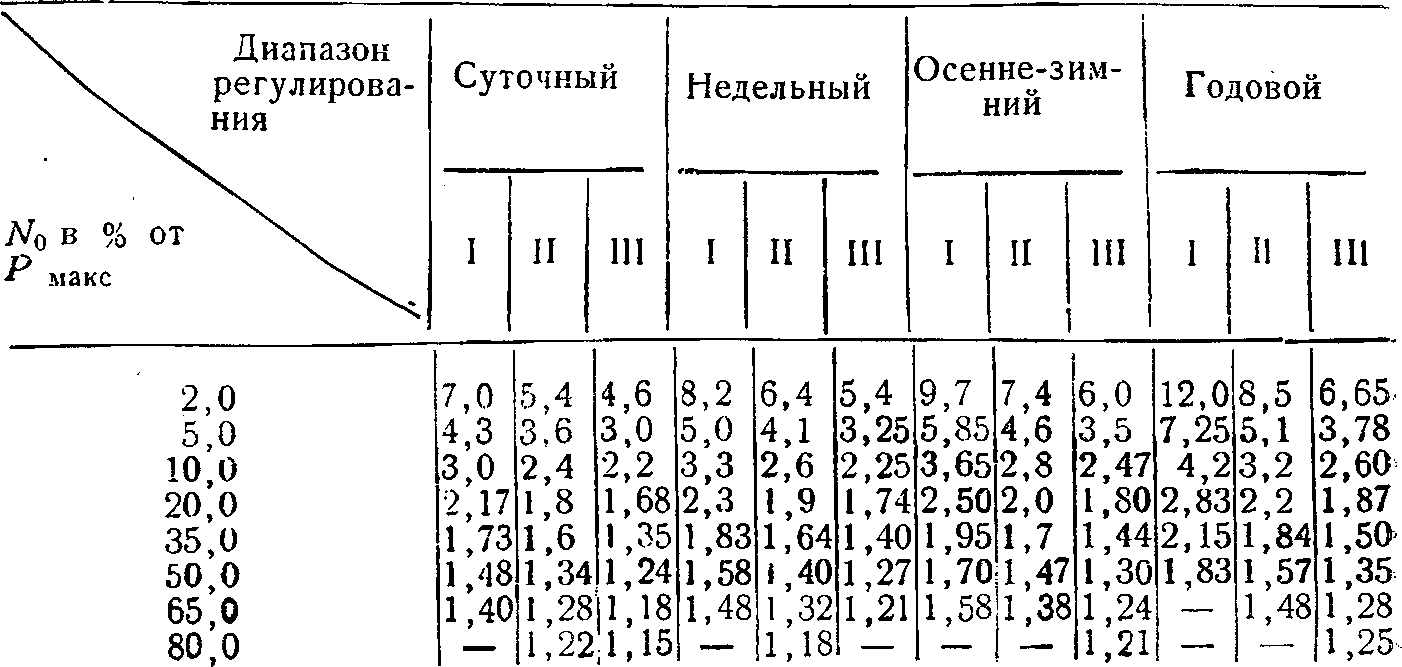
Приведенные графики Μ. П. Фельдмана позволяют определить:

1. Долю участия гидростанции в покрытии максимума графика нагрузки в зависимости от характера ее режима, степени регулирования и соотношения между максимальной потребной и обеспеченной зарегулированной мощностью ГЭС.
2. Пиковую мощность ГЭС АС при известной величине Ν0 в зависимости от соотношения между N0 и Рмакс.

Как нетрудно убедиться, предлагаемые нами расчетные графики для определения коэффициента преобразования обеспеченной зарегулированной мощности ГЭС в располагаемую рабочую, участвующую в покрытии максимума графика нагрузки энергосистемы, являются более обобщенными и позволяют вести соответствующие расчеты при широких диапазонах изменения исходных условий. Следует, однако, оговориться, что это заключение является строго справедливым лишь для случая, когда нет ограничений со стороны водохозяйственных факторов.