ГЛАВА ТРЕТЬЯ
КОНТАКТНОЕ СОЕДИНЕНИЕ И МЕТОДЫ ЕГО ИССЛЕДОВАНИЯ
- ЭЛЕКТРИЧЕСКОЕ СОПРОТИВЛЕНИЕ КОНТАКТНЫХ СОЕДИНЕНИЙ
Первым ученым, который ввел научную систематизацию контактных явлений, был Рагнар Хольм [9], чьи исследования имеют большое теоретическое и практическое значение. Дальнейший вклад в развитие знаний о контактах внесли работы Η. Е. Лысова, О. Б. Брона, В. Мерла, В. Т. Омельченко, Е. И. Кима и др. [5, 10— 12]. Исследованию неподвижных электрических контактов также посвящено большое количество отечественных и зарубежных работ [8—13].
Поведение электрических контактов в этих работах, как правило, исследуется путем изучения физической природы и механизма отказов контактных соединений; при этом текущее состояние контактов описывается уравнением, отражающим физические закономерности. Эксперимент обычно строят в соответствии с так называемым классическим планом, когда все независимые переменные, кроме одной, полагают постоянными, а эту переменную изменяют во всем интервале возможных значений. Таким образом можно оценить изолированное влияние отдельных факторов на электрическое и тепловое сопротивления контактов, которые являются важнейшими параметрами, определяющими надежность работы соединения.
Электрическое сопротивление контактного соединения представляет собой сумму сопротивления R'ш контакт-деталей, образующих нахлесточное соединение, и переходного сопротивления Rпер [10]:
![]() (6)
(6)
Значение сопротивления R'ш контакт-деталей обусловлено конфигурацией контакта, в частности соотношением между толщиной контакт-деталей δ и длиной соединения I. Если длина соединения велика по сравнению с δ, то сопротивление R'ш практически представляет собой сопротивление двух параллельных проводников. При уменьшении длины соединения из-за искривления путей тока сопротивление возрастает. В работе [10] показано, что сопротивление контакт-деталей можно определить как
![]() (7)
(7)
где — сопротивление проводника длиной, равной длине соединения. Значение коэффициента с определяется характером токораспределения в контактном узле. Изучение токораспределения в нахлесточном соединении [8] позволило выявить оптимальную длину и конфигурацию соединения. Установлено, что наиболее типичным значением с является 0,5—0,6.
Решающее влияние на поведение контактных соединений оказывает переходное сопротивление Rпер.
Какова природа этого сопротивления?
Известно, что поверхности контакт-деталей, как и всякого твердого тела, обладают шероховатостью и волнистостью. Самые гладкие металлические поверхности имеют неровности высотой 0,03—0,2 мкм, наиболее грубые — выступы высотой 100—300 мкм.
Наличие шероховатостей приводит к тому, что две поверхности контактируют только в отдельных точках, совокупность которых образует фактическую площадь касания контакта.
Фактическая площадь касания с точки зрения электропроводности состоит из следующих участков [9]:
участок с металлическим контактом, через который ток протекает без заметного сопротивления;
участок с квазиметаллическим контактом — поверхность покрыта топкими пленками (адгезионными и пассивирующими); ток проходит вследствие туннельного эффекта;
участок покрытый органическими пленками и пленками потускнения, практически не проводящими электрический ток.
Исходя из этого проводимость электрического контакта можно определить как сумму проводимостей через зоны металлического и квазиметаллического контактов:
![]() (8) где Rпер — переходное сопротивление; 7?м — переходное сопротивление зоны металлического контакта; Rтун — сопротивление туннельному эффекту зоны квазиметаллического контакта.
(8) где Rпер — переходное сопротивление; 7?м — переходное сопротивление зоны металлического контакта; Rтун — сопротивление туннельному эффекту зоны квазиметаллического контакта.
Полученные в последние годы данные о контакте шероховатых поверхностей позволяют сделать вывод, что сопротивление квазиметаллического контакта значительно превосходит сопротивление металлического контакта и, следовательно, проводимостью через квази- металлический контакт можно пренебречь.
Покажем это на модели одноточечного контакта. Согласно теории Р. Хольма переходное сопротивление (сопротивление стягивания) обусловлено тем, что линии тока вблизи точек касания суживаются и сопротивление увеличивается. Математически эта теория нашла выражение в формуле
![]() (9)
(9)
где р — удельное электрическое сопротивление; а—радиус контактного пятна.
Для алюминиевых проводников (при а≈5-10-6 м)
![]()
Сопротивление туннельному эффекту можно определить как [9]
![]() (10)
(10)

Рис. 17. Определение зоны квазиметаллического контакта

Таким образом, поведение контактных соединений в эксплуатации обусловлено только значением переходного сопротивления зоны металлического контакта (в дальнейшем — переходного сопротивления).
При определении переходного сопротивления контактного соединения плоских проводников многоточечный контакт рассматривают как ряд п независимых друг от друга одноточечных контактов круглой формы с радиусом а. При этом формула (9) принимает вид
![]() . (12)
. (12)
Так как радиус и число контактных пятен обусловлены физико-механическими свойствами и микроструктурой контакт-деталей, задача заключается в изучении зависимости Rпер от этих факторов.
Изучению шероховатости поверхности посвящено много работ [14—17], которые в основном касаются исследования чистоты механической обработки, трения, износа и т. д.
На рис. 18 показан профиль поверхности, содержащий неровности, которые классифицируют следующим образом:
макроотклонениями называют единичные, не повторяющиеся регулярно, отклонения формы поверхности от номинальной (выпуклость, вогнутость, конусность и т. п.);
волнистость — это совокупность периодических, регулярно повторяющихся и близких по размерам (высота 0,03—500 мкм) возвышенностей и впадин, расстояние между которыми (0,25—300 мкм) значительно больше, чем расстояние между микронеровностями;
под шероховатостью понимают совокупность неровностей с относительно малым шагом (0,001—8 мкм) и высотой от 0,03 до 300 мкм.
Площадью контактирования или номинальной площадью касания называют поверхность, ограниченную геометрическими границами контактирующего элемента.
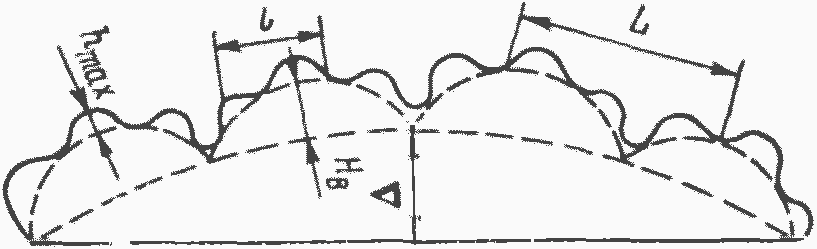
Рис. 18. Профиль поверхности твердого тела: Δ — отклонение профиля; Нв, L — максимальная высота и шаг волн; lmax, l — максимальная высота и шаг неровностей
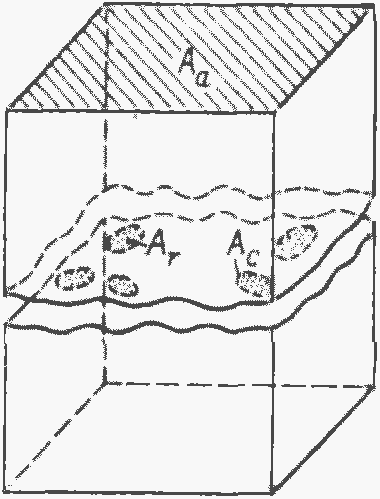
Рис. 19. Площадь контактирования двух шероховатых поверхностей
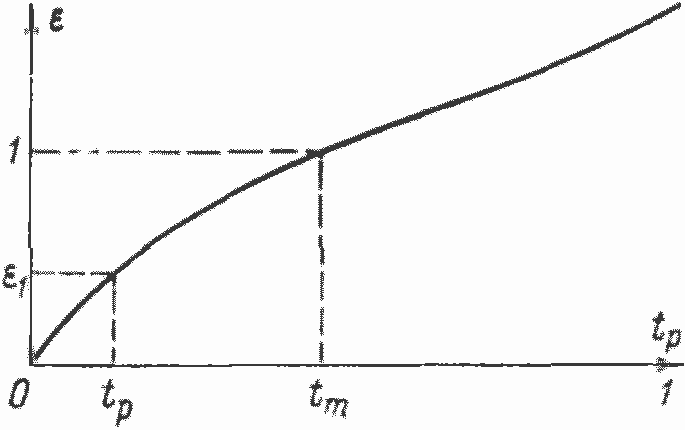
Рис. 20. Опорная кривая шероховатой поверхности
При контактировании твердых тел вследствие волнистости и макроотклонений формы на значительной части номинальной площади касания Аа не происходит соприкосновения микровыступов. Волнистость поверхности определяет те зоны, в которых группируются места соприкосновения этих выступов. Сумма таких зон образует так называемую контурную площадь касания Ас (рис. 19). Наконец, сумму элементарных площадок, расположенных внутри контурной площади, которые образуются в результате соприкосновения и деформации микровыступов, называют фактической площадью касания Аr.
Определение фактической Аr и контурной Ас площадей касания двух твердых тел сопряжено с трудностями, которые обусловлены случайным характером расположения вершин волн и микровыступов. Основой для численного определения характеристик соприкасающихся поверхностей служат их профилограммы, на основании которых строят кривые опорных поверхностей (рис. 20).
Опорной поверхностью называют сумму сечений микронеровностей на некотором участке l0 плоскости, параллельной основанию профиля. Зависимость опорной поверхности от расстояния между плоскостью и основанием профиля выражается кривой опорной поверхности.
Параметры степенной аппроксимации опорной кривой в настоящее время широко применяются для расчетов характеристик контакта шероховатых поверхностей. Это объясняется тем, что степенная аппроксимация опорной кривой позволяет получить формулы, удобные для инженерных расчетов.
Начальная часть кривой до уровня средней линии аппроксимируется в виде [18]

Изучение кривой опорной поверхности для пластического с упрочнением контакта металлов позволило [8] определить радиус а и число п контактных пятен и вывести уравнение переходного сопротивления соединения плоских проводников:
![]()
(13)
где Ν — контактное нажатие (нагрузка); Аа — номинальная (кажущаяся) площадь касания; D1, ξ, τ — константы, определяемые физико-механическими свойствами и микроструктурой контакт-деталей.
Анализ результатов исследования показывает:
- переходное сопротивление обусловлено площадями контактного касания; фактическая площадь касания в шинных соединениях составляет 1—5% поминальной площади; контурная площадь — 25—60%;
- на величину площади касания влияют: пластические свойства материала шин: у мягкого (отожженного) алюминия фактическая площадь составляет 3,6— 4,5% номинальной, а у твердого алюминия—1—3%; контактное давление; чистота обработки поверхностей: при разных видах обработки (драчевый напильник, наждачная бумага, металлическая кардощетка) площади касания практически равнозначны;
- значение переходного сопротивления зависит от микротвердости контактирующих металлов, микрогеометрии поверхностен, а также от контактного нажатия (в степени 0,85—0,95); поверхность рекомендуется обрабатывать по пятому — седьмому классу.
От номинальной площади касания контактных элементов сопротивление зависит незначительно: при увеличении этой площади в 10 раз переходное сопротивление уменьшается на 30—40%.
Проведенные исследования показали, что для шин с поверхностями, обработанными по пятому — седьмому классу и сдавленными напряжением сжатия порядка 10 МПа, переходное сопротивление можно определить из уравнений:

— для соединений медь — алюминий.
Здесь Ν измеряется в ньютонах; Аа — в квадратных миллиметрах; Rпер — в омах.
При выводе уравнений (13) - (16) сделаны следующие допущения и ограничения, связанные с анализом микроструктуры соприкасающихся поверхностей:
1) распределение микровыступов по поверхности металла подчиняется нормальному закону;
2) при соприкосновении контактирующих поверхностей принято, что деформируются только выступы наибольшей высоты и поэтому при расчете использована только верхняя часть кривой опорной поверхности, которая аппроксимируется степенной функцией;
3) микровыступы соприкасающихся поверхностей встречаются на различных уровнях и под различными углами. В расчетах принимается, что все эти контакты расположены в одной плоскости;
4) выступы микрошероховатостей имеют геометрически неправильную форму; в работе с целью упрощения расчетов они заменены сферой;
5) при сближении двух контактирующих поверхностей происходит деформация выступов, которая сопровождается упрочнением материала и нелинейно связана с сопротивлением материала контактов смятию: это вынуждает обратиться к экспериментальным данным, аппроксимирующим в известных пределах рассматриваемый процесс.
Все эти допущения безусловно приводят к некоторой погрешности выведенных соотношений. Определение констант D1, ξ и τ вызывает значительные трудности, и поэтому уравнение (13) малопригодно для инженерных расчетов. Выражения (14) — (16) достоверны только для нормированных напряжений, т. е. для 10 МПа.
Накопленный опыт исследования контактных соединений и контактирования металлов дает возможность достаточно точно решить задачу инженерного расчета электрического сопротивления контактных соединений.
Средний радиус и число пятен контакта можно рассчитать по формулам [19]:

Рис. 21. Параметры шероховатости
mm — средняя линия профиля; аа — линии выступов; bb — линия впадин

В уравнениях (23) и (24) переходное сопротивление определяется физико-механическими характеристиками, параметрами шероховатости и контактным нажатием.
К физико-механическим характеристикам относятся удельное электрическое сопротивление р, фактическое контактное давление Рr и константа A.
Удельное электрическое сопротивление — справочная величина для данных материалов контакт-деталей.
Фактическое контактное давление Рr (давление на пятнах фактического контакта) определяется в зависимости от вида контакта [20]:

Модуль упругости определяется по справочникам для данного материала контакт-деталей. Эта величина малочувствительна к температуре и упрочнению материала при механической обработке.
Микротвердость поверхности контакт-деталей (ГОСТ 9450—76) измеряют непосредственно на контакт-детали или на образцах, изготовленных по той же технологии и из того же материала, что и реальная контакт-деталь. Измерения производят на приборах ПМТ-3 и ПМТ-5. Нагрузку на алмазную пирамиду при измерении На выбирают такой, чтобы глубина внедрения пирамиды, равная 1/7 диагонали отпечатка, не превышала бы высоты выступов шероховатости: Rmах≈5Rа. Микротвердость поверхностных слоев контакт-деталей из-за упрочнения материала при механической обработке может значительно отличаться от твердости материала в объеме. Поэтому использование в расчетах твердости по Бринеллю вместо микротвердости приводит к существенной ошибке. Микротвердость зависит от температуры. Зная микротвердость H при комнатной температуре Θ0, микротвердость при температуре Θ можно рассчитать по формуле
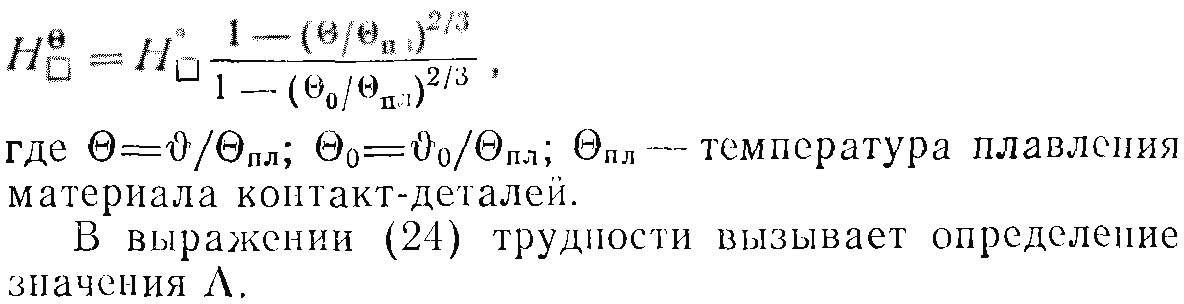
При пластической деформации микровыступов шероховатой поверхности происходит разрушение оксидной пленки и в контакт вступают участки поверхности, не покрытые пленками, через которые проходит основная доля носителей заряда. Наиболее вероятный характер деформации отдельных микровыступов — смятие. Поэтому рассмотрим в качестве модели смятие отдельного пластинчатого клиновидного выступа плоской плитой (рис. 22). На рис. 22 показана половина сминаемого клина. Из анализа поля линий скольжения видно, что все точки в зоне ВЕС, в том числе и точка В, движутся параллельно линии ЕС. Поэтому точка В' — это положение точки В на боковой поверхности клина АС до смятия (В'В//СЕ). Точка А после смятия займет положение А'. Относительное увеличение поперечного размера поверхностного клина, находящегося в контакте, очевидно,
![]()
Величина А и есть доля контактной поверхности, свободная от пленок, так как вновь возникшие в процессе смятия участки поверхности не могли покрыться поверхностными пленками. Поперечный размер поверхностного клина Л можно выразить через угол при вершине клина 0. Расчетное выражение получатся сложным, поэтому предлагается простая аппроксимирующая формула:
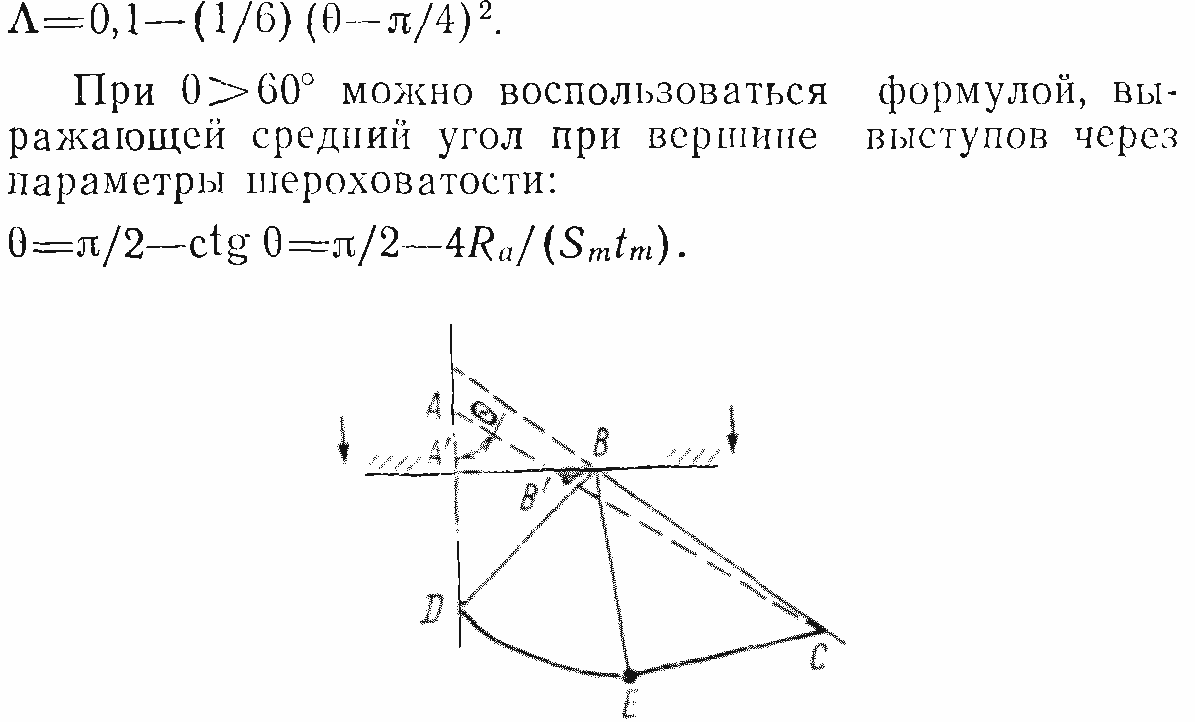
Рис. 22. Смятие клина плоской плитой

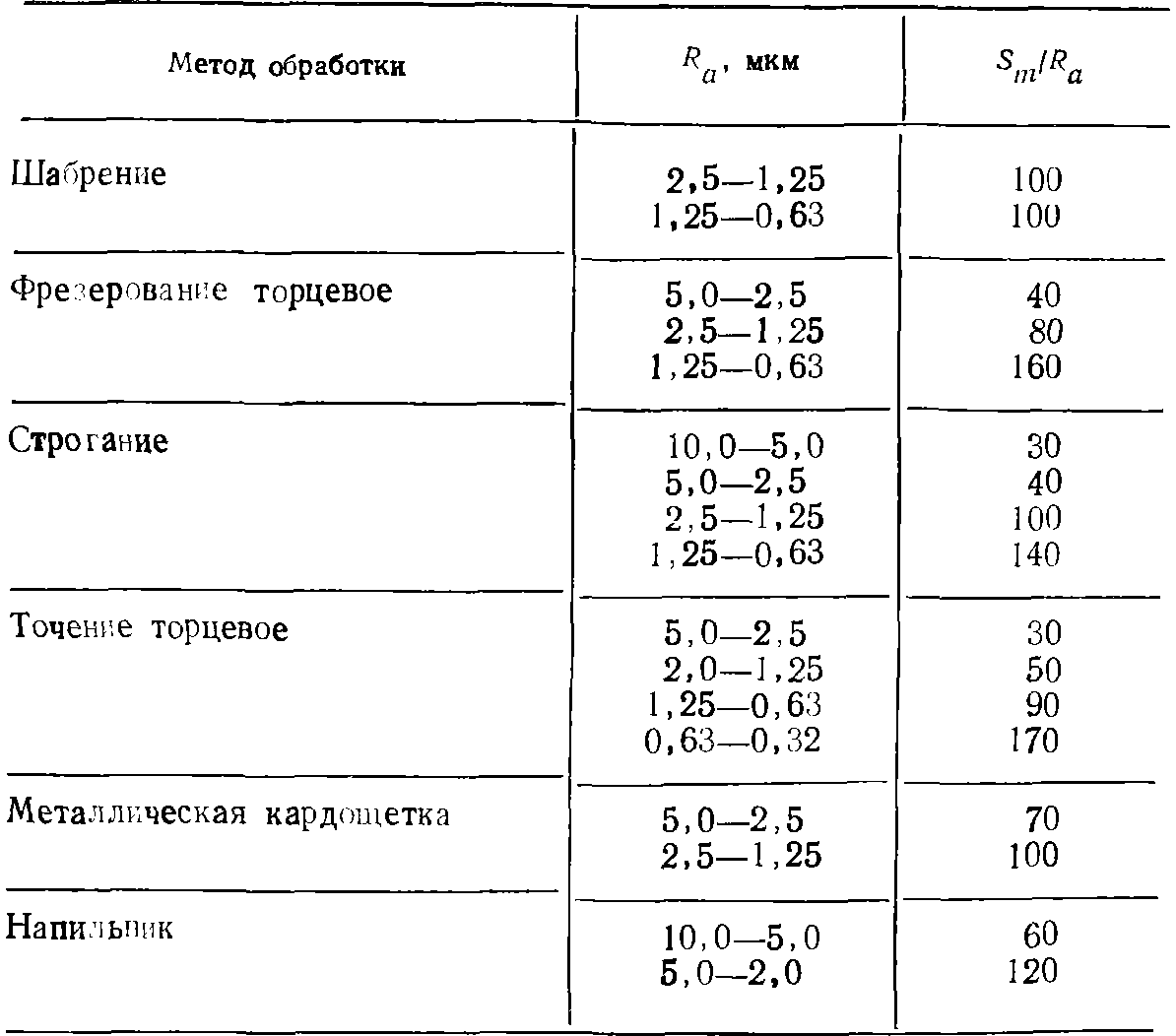
Примечание. Относительная опорная длина tm=0,4-0,6.
Таким образом, рассмотрены все параметры, входящие в уравнение (24). Так как для контакт-деталей из меди, алюминия и его сплавов при указанных выше моментах затяжки болтов, как правило, имеет место пластический контакт, т. е.![]() , выражение
, выражение
(24) можно представить в виде (при![]() )
)
![]() (30)
(30)
Таблица 12
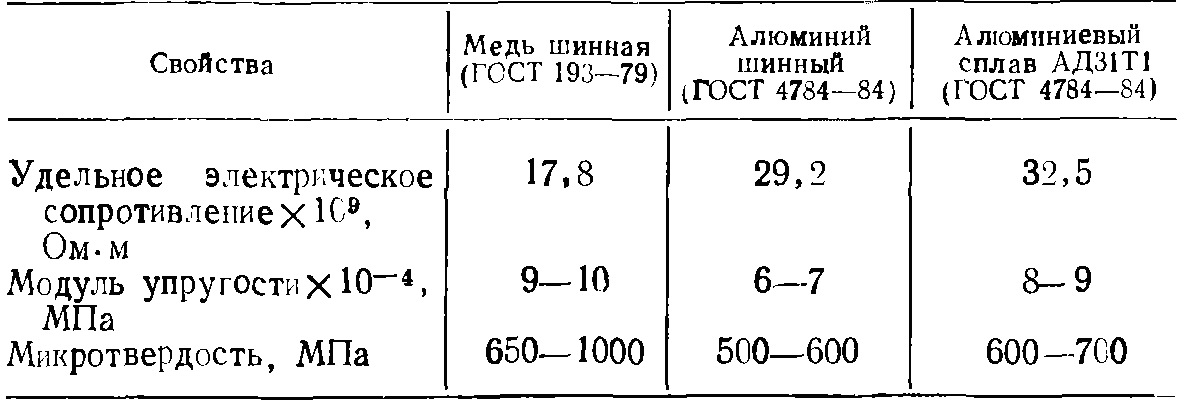
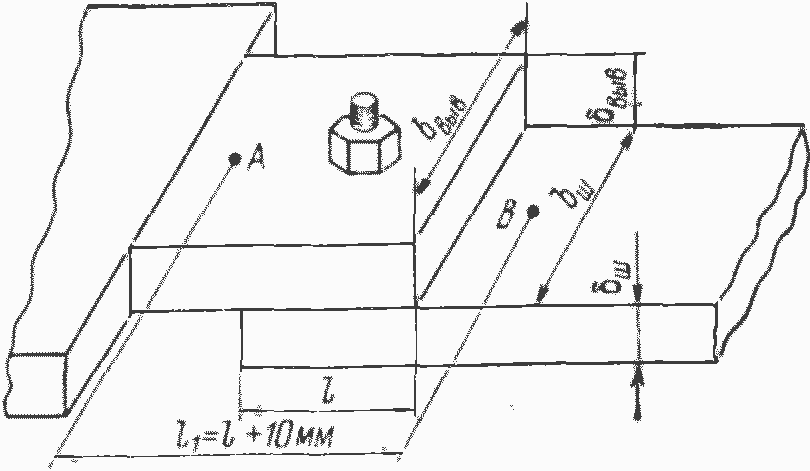
Рис. 23. Расчетная модель контактного соединения


Анализ этих зависимостей позволяет оптимизировать параметры контактного соединения.
В заключение следует отметить, что формулы (24) и (30) дают возможность определить усилие сжатия контактного соединения при заданном значении переходного сопротивления.
В соответствии с ГОСТ 10434—82 отношение начального электрического сопротивления Rк.c контактных соединений к сопротивлению Rш контакт-детали меньшей проводимости, длина которой равна длине соединения, не должно превышать 1, т. е. должно выполняться условие Rк.с=Rш. Принимая Rк.с=Rш, с=0,5, из соотношений (6) и (7) получаем Rпер=0,5Rш. Тогда из выражения (30) можно определить контактное нажатие

Полученное значение крутящего момента на 10% превышает значение, рекомендованное в ГОСТ 10434—82. Для обеспечения повышенных крутящих моментов следует применять болты класса прочности 5.8 и выше, предпочтительно — класса 8.8.

