Рассматривая контактное соединение как многоточечный контакт с п пятнами и радиусом контактного пятна а, можно считать, что Rпep=f(а, п). Ряд теоретических предпосылок указывают на то, что во времени число контактных пятен практически не изменяется. Тогда, зная зависимость Rпep=f(a) и характер изменения радиуса контактного пятна во времени a=f(t), можно сопоставить поведение контактов из различных металлов, например меди, алюминия, алюминиевых сплавов, а также прогнозировать срок их службы.
Для расчета электрического сопротивления обычно принимается модель контакта радиусом rк (рис. 32), на которой расположены n одинаковых круглых токопроводящих площадок с радиусом а0.

Рис. 32. Схема микровыступа цилиндрической формы (а) и модель многоточечного контакта (б)
Сопротивление такого соединения может быть определено по выражению

Однако использование соотношения (58) для алюминия и его сплавов приводит к большой погрешности.
Принимая во внимание сказанное, а также учитывая, что измерение толщины пленок примерно 1—5 нм представляет определенную сложность, законы роста толщины пленок на алюминии и его сплавах определены с помощью эллипсометрии [31]. Этот поляризационно-оптический метод исследования поверхностей основан на изучении изменения поляризации света при его взаимодействии с поверхностью. Вопросы распространения,
преломления и отражения света здесь рассматриваются с позиций электромагнитной теории, в основе которой лежат уравнения Максвелла.
Основное уравнение эллипсометрии для отраженного света записывается в виде
![]()
где Rp, Rs — френелевские коэффициенты; ψ — арктангенс отношения френелевских коэффициентов для р- и s-поляризаций; Δ — фазовый сдвиг между р- и s-компонентами, возникающий при отражении; р и s — направления компонента электрического вектора световой волны, соответственно, в плоскости падения и перпендикулярно ей.
При исследовании отражающих систем методом эллипсометрии решаются три задачи: вычисляются поляризационные углы ψ и Δ на основе принятой отражающей системы, которая характеризуется определенными параметрами; экспериментально определяются поляризационные углы ψ и Δ; производится сравнение вычисленных поляризационных углов с их экспериментальными значениями.
Для измерения двух параметров эллипса ψ и Δ применяются различные схемы эллипсометров, например схема с визуальной регистрацией (рис. 33).
Эллипсометр представляет собой двухплечий оптический прибор, в котором свет источника ИС линейно поляризуется призмой Пр, отражается от образца М, проходит через анализатор А (представляющий собой линейно-поляризующее устройство, аналогичное призме Пр) и регистрируется визуально через телескопическое устройство О. Между поляризатором Пр и анализатором Ά устанавливается компенсатор К (компенсатор Сенармона), изменяющий соответствующим образом фазовый сдвиг между р- и s-компонентами.
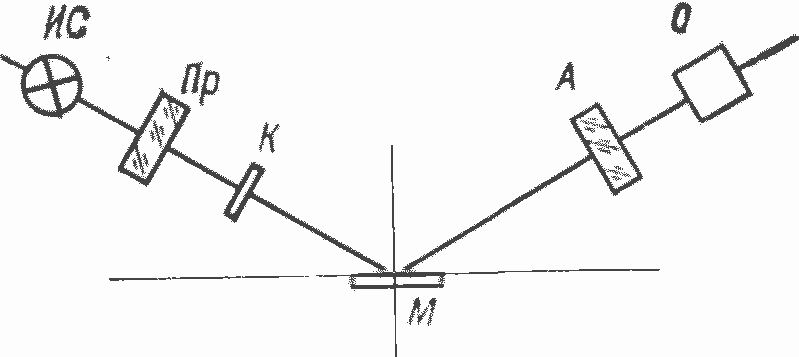
Рис. 33. Схема эллипсометра
Под компенсатором понимается двоякопреломляющая слюдяная пластина, в которой известны направления быстрой и медленной осей, т. е. направления колебаний электрического вектора световых волн, распространяющихся быстрее или медленнее относительно друг друга. Ориентация элементов Пр, К и А задается с помощью азимута — угла между плоскостью падения и характерным направлением данного элемента, отсчитываемого наблюдателем, смотрящим навстречу лучу. Все поляризующие элементы крепятся в градуировочных оправках для измерения азимутов. Компенсатор К может быть установлен как до, так и после образца. Измерение параметров эллипса осуществляется вращением двух из трех поляризующих элементов при фиксированном третьем элементе. Например, К устанавливается быстрой осью под углом 45° к плоскости падения света. Вращением Пр и А добиваются минимума пропускания отраженного света и фиксируют значения азимутов.
Затем поляризатор Пр поворачивается на 90° и процедура повторяется. Получают две пары отсчетов. Эти измерения дают возможность определить tgψ, Δ.
Образцы для измерения готовились следующим образом. Из пластин соответствующего сплава вытачивались диски диаметром 10 мм и толщиной 1,5 мм. Затем одна из торцевых поверхностей образца полировалась пастой ГОИ на смоляном полировальщике, как это принято при изготовлении металлографических шлифов.
Образцы помещались в термопечь, где нагревались до заданной температуры. Через каждые 30 мин образец извлекался из печи, охлаждался на воздухе, проводились измерения, после чего он снова устанавливался в термопечь. Поскольку образец имел небольшие размеры и массу, время установления необходимой температуры было примерно 1 мин.
Необходимой частью работы являлось определение оптических констант-коэффициентов преломления п3 и отражения подложки k3п. Имеющиеся в литературе данные о константах чистого алюминия противоречивы, а данные об исследуемых сплавах вообще отсутствуют. Отыскание констант подложки проводилось методом подбора с использованием прямых программ для вычисления ψ и Δ. Для этого снимались многоугловые (для пяти углов падения — 83, 80, 77, 73. 70°) зависимости ψ и Δ в начальном состоянии образцов.
Предполагая, что на поверхности сплава имеется пленка оксида с коэффициентом преломления n2≈1,7 и толщиной 2—4 нм, все параметры системы подбирались такими, чтобы удовлетворить экспериментальной многоугловой зависимости. Таким образом были найдены толщина оксидного слоя и его коэффициент преломления, а также оптические константы сплавов.
На рис. 34 приведены экспериментальные зависимости для ψ и Л для сплава ЛД31Т1. До начала эксперимента на поверхности сплава имелась пленка, образовавшаяся при нормальной (комнатной) температуре. Как видно из рисунка, в течение первого получаса наблюдается релаксационный процесс, по окончании которого начинается систематический рост оксидной пленки. По истечении примерно 4—5 ч начинается иной процесс, когда растут одновременно ψ и ∆. Такое изменение ф и Δ не может быть связано с ростом пленки. Очевидно, после 4—5 ч начинают меняться константы сплавов, что можно объяснить сегрегацией примесей из объема к поверхности образца (см. ниже).
Таким образом, можно считать, что в чистом виде роет оксидной пленки наблюдается в промежутке 1— 3,5 ч. Действительно, обработка экспериментальных значений ψ и Δ в этом интервале дает значение показателя преломления слоя оксида для сплава АД31Т1, равное 1,68+0,01.
Зависимость толщины оксидной пленки от времени выдержки приведена па рис. 35. Эти зависимости представляют собой апериодические кривые 2-го порядка и могут быть, описаны уравнением (суммой двух экспонент с различными постоянными времени)

Выполненные исследования показали, что зависимость (59) не может быть использована для оценки срока службы контактов.

Рис. 35. Изменение толщины оксидной пленки от времени (сплав АД31Т1) при температуре 373 К (кривая 1), 353 К (кривая 2) и 333 к (кривая 3)
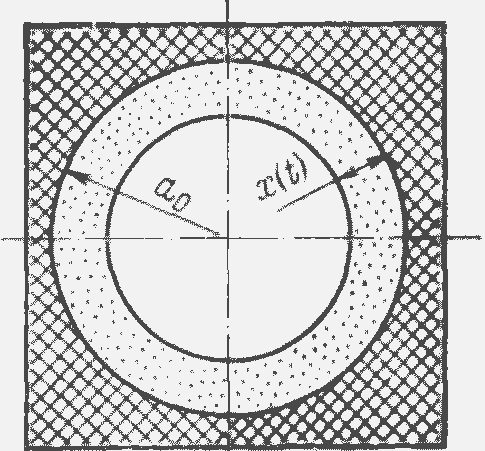
Рис. 36. Модель контакта оксидной пленки
Для решения этой задачи используем явление диффузии в контактных соединениях.
Рассмотрим модель контакта, показанную на рис. 36. Здесь заштрихована область окисленной поверхности, точками обозначена область проникновения пленки вследствие диффузии в зону контакта.
В начале рассмотрим случай, когда контактные элементы сжаты постоянным и стабильным механическим усилием без вибрации, а электрический ток через контакт не протекает. Примем следующие допущения: контактная граница имеет однородные характеристики по всей поверхности контакта, оксидная пленка и диффундирующий слой между элементами контакта имеют кольцевую форму; пленка растет вследствие диффузии только в радиальном направлении.
Для такого контакта через время t после ввода в эксплуатацию переходное сопротивление будет определяться соотношением
![]() (60)
(60)
где Rпep(t) — сопротивление в момент времени t; Rпep(0) — сопротивление в момент времени (после окисления); а0 — радиус металлического пятна касания в момент времени t≈0; x(t) — глубина диффузионного проникновения пленки в зону металлического пятна касания через время t.
Оценим глубину проникновения x(t) диффундирующего вещества. Примем простейшую модель диффузии (рис. 37). Здесь заштрихованным кружком показаны атомы оксида, чистым кружком — атомы металла.

Рис. 37. Диффузионная модель
Перемещение диффундирующего атома оксида происходит путем случайного (типа броуновского) блуждания по узлам кристаллической решетки, элементарным актом которого является перескок из одного положения локального равновесия в другое, соседнее, т. е. обмен местами с неокисленными атомами. Этому процессу препятствует межатомное взаимодействие, вследствие чего перескок может совершить только атом, обладающий энергией активации, которая необходима для «расталкивания» соседних атомов при перескоке. Диффундирующий атом получает энергию активации U вследствие тепловых флюктуаций после времени ожидания:
![]() (61)
(61)
где τ0 — период тепловых атомных колебаний; Θ — абсолютная температура; К — газовая постоянная.
Диффундирующий атом в равных условиях совершает перескоки «вперед — назад» с равной вероятностью, однако наличие градиента концентрации оксида (избыток его на поверхности по сравнению с объемом) порождает термодинамическую движущую силу, которая вызывает «расплывание» с поверхности оксида.
Рассмотрим простейшее математическое описание кинетики процесса диффузии. Пусть атом в положении 1 (рис. 37) совершает перескок вперед, т. е. в положение 2, с вероятностью р и назад, т. е. в положение 3, с вероятностью g. Перескоки осуществляются через интервал времени τ'. Приращение координаты х, соответственно положительное или отрицательное, при каждом скачке по абсолютному значению равно межатомному расстоянию μ.
Для вероятности κ(х, ί) найти атом в координате х в момент времени f можно, записав уравнение, являющееся формулой полной вероятности:

Контактное нажатие, во-первых, определяет площадь пятна касания, во-вторых, значение N влияет на скорость диффузии, увеличивая барьер энергии активации

Рис. 38. Изменение переходного сопротивления контактного соединения во времени для алюминия (кривая 1), алюминиевого сплава (кривая 2) и меди (кривая 3)
![]()
Аналогичным образом построены кривые для соединений медных и алюминиевых шин.
Значения Rпер(t) хорошо совпадают с экспериментальными значениями, полученными в результате четырехлетних наблюдений за соединениями размером 6х60 мм из алюминия, алюминиевого сплава АД31Т1 и меди с покрытием оловом рабочих поверхностей. Это подтверждает применимость сформулированных предположений для описания процесса изменения Rпер во времени.
Предложенный подход позволяет прогнозировать срок службы контактных соединений из различных проводниковых материалов.
Изготовление контактных соединений в соответствии с требованиями, изложенными в гл. 2, а также выполнение рекомендаций по их эксплуатации [8] обеспечивают достаточно высокую работоспособность соединений.

