Имеются три главных отличия моделей отбора с анализом решение от обычных моделей отбора. При использовании анализа решений; ценностные установки четки, точны и количественно определены недостатки этих установок, рассмотренные в § 4.2, либо отсутствуют, либо их влияние существенно уменьшено;
применяемые критерии более тесно связаны с основными целями выбора площадок для энергетических объектов.
Модели отбора с анализом решений можно разделить на две группы, между которыми имеется много общего. В моделях компенсационного отбора учитываются ценностные соотношения между критериями отбора, а также придается большее значение, чем в обычных моде, лях отбора, иерархии различных критериев. Однако в этих моделях все еще применяются предельные уровни критериев. В моделях сравнительного отбора также используются ценностные соотношения, но отбор территории производится только тогда, когда сравнение двух территорий показывает, что одна из них не может содержать наилучший вариант площадки. В отдельных случаях используется комбинация этих двух подходов.
4.3.1. Выбор четких ценностных установок.
Важная цель каждого анализа решений, в моделях отбора состоит в том, чтобы гарантировать точность и ясность всех ценностных установок, необходимых для отбора. Особое внимание уделяется тем установкам, которые требуют качественной мотивировки при выборе района, представляющего интерес, или выборе шкалы.
Что касается района, представляющего интерес, то необязательно накладывать на него ограничения в самом начале исследования, т. е. при его назначении, сводя его территорию к определенной административной или географической зоне. Обычно в основе подобных ограничений лежит интуитивное представление, что вне этого района нет удовлетворительных площадок. Но если это действительно так, то модели отбора, рассматриваемые в п. п. 4.3.2 и 4.3.3, позволяют это установить. Это исключает необходимость начинать с назначения района, представляющего интерес, создавать строгие обоснования площадок, которые будут в конечном счете выявлены, обеспечивать информацию для анализа чувствительности результатов к исключенным территориям.
В качестве примера предположим, что в исследовании для WPPSS в качестве района, представляющего интерес, рассматривалась вся территория США и Канады. Так как целью предполагаемого строительства электростанции является электроснабжение штата Вашингтон, то критерии отбора, основанный на стоимости передачи электроэнергии, сразу исключил бы значительную территорию из рассмотрения как не представляющую интереса. Такой же результат может быть получен и при использовании совсем другой процедуры.
Когда шкалы или предельные уровни критериев выбраны, они должны быть пояснены и обоснованы. Это означает, что набор критериев должен включать в себя и государственные нормы, определяющие, например, необходимые расстояния от геологических разломов земной коры.
Кроме того, предполагается, что соотношения между шкалами критериев и их предельными уровнями, а также основные цели сооружения энергетического объекта достаточно ясны. При соблюдении этих условий облегчается оценка произведенного отбора площадок заинтересованными лицами.
Модели отбора с анализом решений, так же как и обычные модели отбора, во многом опираются на заключения специалистов в различных областях, связанных с размещением предприятий. По соображениям, изложенным в п. 4.2.1. полезно использование экспертных оценок при выборе возможных площадок в пределах возможных зон. Однако обычно важно этот выбор обосновать, что требует составления обоснованных экспертных оценок и ценностных установок. Эта задача облегчается, если территория рассматриваемой возможной зоны достаточно мала и число возможных площадок в ней невелико. Если же возможная зона велика, применение формализованной модели отбора позволяет выделить из нее для выбора площадок существенно меньшую территорию. Количество критериев отбора в такой модели должно быть значительно меньше количества критериев для обычной модели отбора, поскольку начальная рассматриваемая возможная зона намного однороднее, чем весь район, представляющий интерес.
4.3.2. Модели компенсационного отбора
Проиллюстрируем модели компенсационного отбора по материалам исследований для WPPSS. Согласно табл. 3.1 из-за расходов на перекачку воды площадки, расположенные дальше 16 км от источника воды и выше 250 м над ним, должны быть исключены из дальнейшего рассмотрения. Это показано на рис. 4.4, а.
Предположим, что годовые расходы по перекачке охлаждающей воды, необходимой для намеченной электростанции, на расстояние 16 км составляют 5 млн. долл., а годовые затраты по перекачке этой воды на высоту 250 м равны 4 млн. долл. Далее допустим, что затраты пропорциональны соответственно расстоянию и высоте. Таким образом, общие годовые затраты, млн. долл., на перекачку воды выражаются через расстояние d и высоту h простой формулой
![]() (4.1)
(4.1)
где d — расстояние, км; h — высота, м.
Если исключать из рассмотрения площадки, для которых годовые затраты, например, более 7 млн. долл., получается результат, приведенный на рис. 4.4, б.
Сравнивая рис. 4.4, а и б, можно сделать несколько интересных выводов. В каждом варианте имеются площадки, которые признаются допустимыми, но отвергаются в другом варианте. В модели стандартного отбора в качестве возможной принимается площадка (точка A на рис. 4.4, а) с расходами 9 млн. долл, в год на перекачку воды, но отвергается площадка (точка В) с расходами примерно 4 млн. долл, в год. При применении модели компенсационного отбора — наоборот, что, конечно, более разумно.
Если воспользоваться терминологией п. 4.2.4, затруднение состоит в том, что критерии стандартного отбора на рис. 4.4, а не согласованы. Увеличение расстояния свыше 16 км, чему соответствуют годовые затраты в 5 млн. долл., или же увеличение высоты более чем до 250 м, чему соответствуют затраты в 4 млн. долл., являются основанием для исключения площадок.

Рис. 4.4. Сопоставление стандартного (а) и компенсационного (б) отборов:
1 — область неприемлемых значений из-за высоты не менее 250 м; 2 — область неприемлемых значений из-за расстояния не менее 16 км; 3 — область неприемлемых значений из-за затрат на перекачку, больших 7 млн. долл.; 4 —линия, соответствующая затратам на
перекачку 7 млн. долл.
Этот пример обладает двумя характерными особенностями, которые следует подчеркнуть. Во-первых, модель компенсационного отбора располагается в иерархии моделей отбора выше, так как в ней комбинируются два критерия. Критерий более высокого уровня — общая стоимость перекачки воды— является более точным экономическим показателем, чем критерии более низкого уровня, какими являются высота над источником воды или расстояние от него. Во- вторых, для разработки способа комбинирования критериев в большей степени требуются профессиональные соображения, чем ценностные установки. На основании профессиональных соображений расчет расходов по перекачке воды по горизонтали и вертикали проводится по одной простой формуле (4.1). Ценностная установка понадобилась для выбора предельного уровня в 7 млн. долл., что находится в пределах 4—9 млн. долл., использованных в модели стандартного отбора. Нетрудно распространить этот пример на случай нескольких критериев. Допустим, что имеются критерии отбора Z1, Z2 ,.., Zn, причем в основе каждого из них лежит категория стоимости. Задача состоит в том, чтобы определить функцию с (z1, z2, ..., zп), которая соотносит стоимость с некоторыми уровнями Ζ1, Ζ2, ..., Zn соответствующий критериев отбора. Такая модель требует экспертных оценок и данный для ее составления. Чем больше критериев отбора удается таким образом скомбинировать, тем меньше вероятность того, что недостатки моделей стандартного отбора, рассмотренные в § 4.2, будут существенно влиять на исследование.
Имеется другой тип моделей компенсационного отбора, в которых, чтобы скомбинировать критерии более низкого уровня их иерархии, следует больше опираться на ценностные установки, чем на соображения экспертов и данные. Для иллюстрации одновременного использования моделей компенсационного отбора разного типа следует снова обратиться к сведениям, приведенным в табл. 3.1. Предположим, что уже записано уравнение (4.1) для стоимости перекачки воды.
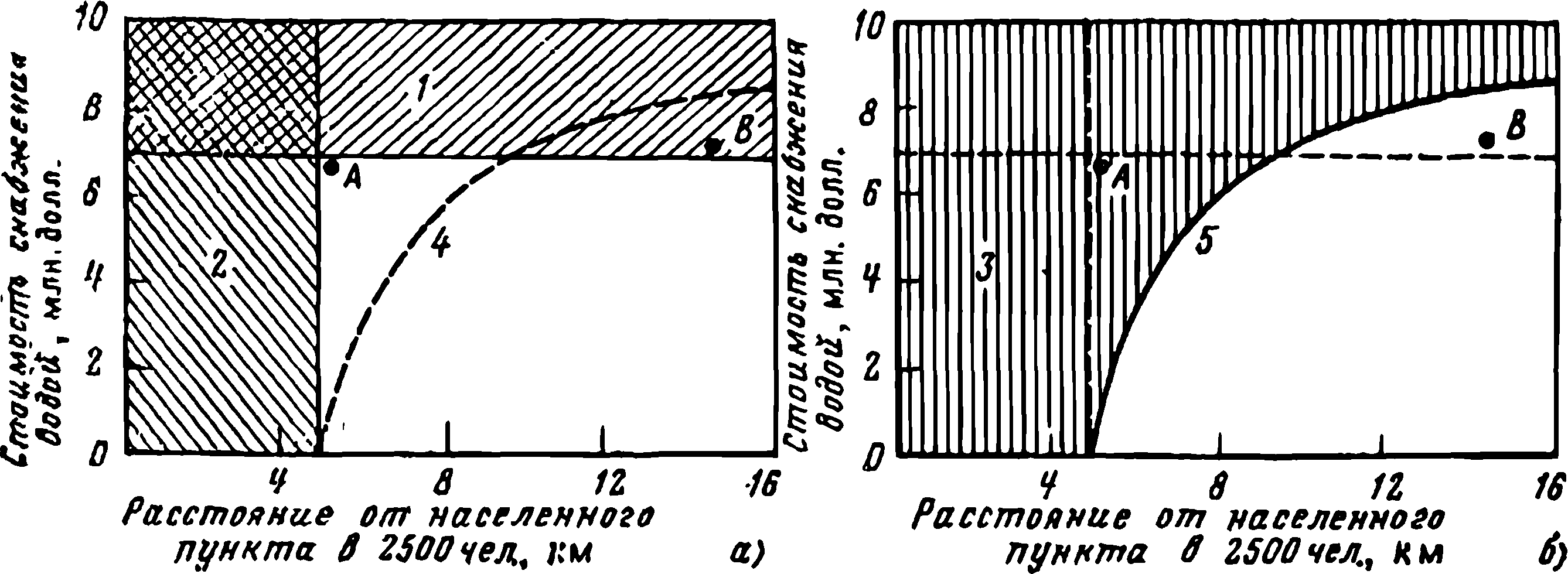
Рис. 4.5. Применение ценностных установок при компенсационном отборе:
а - стандартный отбор; б — компенсационный отбор; 1 — область неприемлемых значений из-за стоимости; 2 —область неприемлемых значений из-за расстояния от населенного пункта; 3 —область неприемлемых значений по сочетанию стоимости и расстояния; 4 — условная кривая безразличия; 5 — кривая безразличия
Допустим, что эта стоимость является критерием, по которому производится отбор, (т. е. что она сильно различается для разных площадок), и ее можно грубо определить для каждой площадки. Дополнительно предположим, что учитывается другой критерий — расстояние от площадки до пункта с населением более 2500 чел. Теперь желательно составить модель компенсационного отбора из обоих критериев отбора: стоимости перекачки воды и расстояния от электростанции до указанного населенного пункта.
Не существует профессиональных соображений или данных для составления оптимальной комбинации из этих двух критериев. Необходимы ценностные установки. Очевидно, что более предпочтительны площадки с меньшими затратами и отстоящие дальше от населенных пунктов. На рис. 4.5, а показано применение обычных методов отбора с использованием предельных уровней критериев, равных 5 км и 7 млн. долл. Из рис. 4.5 следует, что площадка А со стоимостью перекачки воды около 7 млн. долл, и расстоянием до населенного пункта всего 5,2 км признается допустимой, а площадка В со стоимостью перекачки воды 7,1 млн. долл., и расстоянием 13,5 км исключается из дальнейшего рассмотрения.
Используя ценностные установки, можно определить кривую безразличия (равноценности), показанную на рис. 4.5, б. Эту кривую можно рассматривать как границу приемлемости. Применение такой
кривой безразличия дает согласование в смысле, указанном в п. 4.2.4 в то время как в модели стандартного отбора предельные уровни согласованы. Если бы они были согласованы, кривая безразлично асимптотически приближалась бы к горизонтальной линии, соответствующей 7 млн. долл. Только тогда нежелательность затрат на пере, качку в 7 млн. долл, будет эквивалентна расстоянию 5 км от населенного пункта с 2500 жителями.
Заметим, что, так же как и в случае рис. 4.4, некоторые площадки приемлемые для одной модели, исключаются для другой. В частности площадка А при компенсационном отборе становится неприемлемой, а площадка В приемлемой. Происходит это вследствие того, что компенсационном отборе используются согласование и ценностные соотношения критериев.
Имеется дополнительная ценностная установка о том, как проводить кривую безразличия. Известно, что согласно нормативу все площадки должны находиться на расстоянии 5 км или более от пунктов с населением более 2500 чел. В силу этого кривая безразличия может пересекать ось расстояний в точке, соответствующей не менее 5 км. Однако кривая может пересекать эту ось и в точке, соответствую, щей более 5 км.
В общем случае компенсационный отбор с применением кривой безразличия происходит следующим образом. Имея критерии отбора Ζ1, Ζ2, ..., Ζn с соответствующими уровнями z1, z2, ..., zn, выбирают приемлемый предельный уровень, характеризуемый некоторым набором уровней z, определяющих границу между приемлемыми и неприемлемыми площадками. Далее с применением дополнительных ценностных установок через точки z' проводится кривая безразличия. Площадки с показателями более благоприятными, чем z', являются приемлемыми, другие исключаются из рассмотрения.
Модели компенсационного отбора свободны от таких, нередко присущих моделям стандартного отбора, недостатков, как несогласованность критериев или несоответствие ценностным соотношениям. Однако и для применения этих моделей по-прежнему необходим выбор предельных значений. Но это предельное значение устанавливается лишь для высших уровней иерархии целей отбора, и поэтому его значение, по которому отвергаются площадки, существенно снижено.

