ОЦЕНКА ВОЗДЕЙСТВИЙ ЭНЕРГЕТИЧЕСКОГООБЪЕКТА
Следующий этап анализа должен оценить относительную приемлемость последствия х = (x1, х2, ..., х6), где x1 определяется как количественная мера, значение или уровень Хi, i = 1, 2,..., 6. Таким образом, например, х6 может быть равно 8 млн. долл. — мера измерения критерия Х6. Необходимо определить функцию полезности и (х1, х2,.... х6) через шесть критериев табл. 3.2.
Структура ценностей, обсуждаемая ниже, предложена экспертами фирмы WCC. Она базировалась на их понимании точки зрения энергетической компании WPPSS. Для каждого критерия функция полезности оценивалась с использованием знаний наиболее квалифицированных членов группы выбора площадки (т. е. экспертов).
Допущения о структуре многокритериальной функции полезности и ценностные соотношения между критериями были совместно определены ведущими членами группы проектировщиков. Итоговая структура ценностей обсуждалась и проверялась компанией WPPSS и, следовательно, отражает ее точку зрения. Другие точки зрения рассматривались в процессе проведения анализа чувствительности.
Как упоминалось в л, 2.3.4,: процедура определения функции полезности может быть разбита на пять этапов.
На первой стадии анализа группа по выбору площадки рассмотрела терминологию и конечную цель. В практике, как показано ниже, проверки и повторение этапов необходимы на всем протяжении процедуры оценки полезности.
Определение общей структуры предпочтений
Важным шагом в определении вида функции полезности является исследование разумности предположения о независимости предпочтений и полезностей. Ограниченная определенными условиями шестикритериальная функция полезности выражается в простой функциональной форме шестью однокритериальными функциями полезности, Покажем это на примере. Дополнительные подробности по упомянутым условиям независимости приведены в § 7.2.
Два критерия независимы по предпочтениям от других критериев, если порядок предпочтения для комбинации не зависит от фиксированных уровней других критериев. Рассмотрим дифференциальные годовые затраты Х6 и воздействие на лососевых Х2. Группа по выбору площадки задалась вопросом, какой уровень Х6 со 100%-ной гибелью лососевых в реке со 100 000 лососей равноценен варианту с затратами в 40 млн. долл., но без потерь лососевых при условии, что четыре других критерия находятся на их лучших уровнях. Оказалось, что этот уровень — 20 млн. долл. Затем рассмотрен тот же вопрос с другими критериями на их худших уровнях. Оказалось, что результат был также 20 млн. долл. Путем рассмотрения других пар независимых точек можно установить, что ценностное соотношение между (Х6, Х2) может быть независимым от уровня других критериев. Так как группа по выбору площадки пришла к выводу о независимости предпочтений после серии вопросов вышеуказанного типа о критериях, было принято, что ценностные соотношения между двумя критериями не зависят от уровня других критериев. Таким образом, каждая пара критериев рассматривалась независимой по предпочтениям по отношению к другим парам.
1 Лотерея определяется совокупностью возможных последствий (исходов) и их вероятностью (шансом).
Оценка была проведена при помощи методик, описанных в следующем
разделе. Установлено, что относительное предпочтение для лотерей, включающих в себя неопределенность только в последствиях для Х3, не зависит от других критериев. Таким образом, критерий Х3 независим по полезности от других критериев.
Вышеупомянутые условия независимости, которые были расценены как приемлемые, позволили прийти к выводу, что вид функции полезности должен быть либо

где и и fi — функции полезности, изменяющиеся от 0 до 1; k — весовые коэффициенты, причем 0 < kг < 1, a k >—1. Уравнение (3.2) представляет собой аддитивную функцию полезности, а уравнение (3.3) — мультипликативную функцию полезности. Более подробно об этом говорится в § 7.2.
В результате устанавливается, что многокритериальная функция полезности может быть полностью определена однокритериальными функциями полезности ui и значениями весовых коэффициентов ki. Как будет показано ниже, для данного исследования была принята мультипликативная функция полезности. Хотя достаточно только одного предположения о независимости по полезности для того, чтобы прийти к заключению о том, выбирать ли (3.2) или (3.3); это условие было подтверждено и для других критериев в процессе постоянной проверки.
Оценка однокритериальной функции полезности
Оценка функций полезности для критериев, измеряемых естественной шкалой, т. е. u1, u2, и4 и и6, была сделана способом стандартной лотереи 50—50 1, обсуждаемой в § 7.5. Например, рассматривая (с целью выбора предпочтения), с одной стороны, ряд уровней Х6, а с другой — результаты этой лотереи с исходами 0 и 40 млн. долл, дифференциальных затрат, было решено, что для компании WPPSS лотерея с указанными исходами и ее детерминированный эквивалент, соответствующий уровню затрат в 22 млн. долл., равноценны. Таким образом, поскольку полезность есть мера предпочтения, лотерея и ее детерминированный эквивалент должны иметь равные ожидаемые полезности. В соответствии с (3.3) устанавливаются начальное значение и масштаб, полезность наихудшего значения Х0 40 млн. долл, принимается равной 0 (см. табл. 3.2), а полезность наилучшего значения Х0 0 млн. долл. — равной 1.
1 Лотерея 50—50 — лотерея с вероятностью (шансом) исхода (выигрыша), равной 0,5, или 50%. (Прим. р е д.)
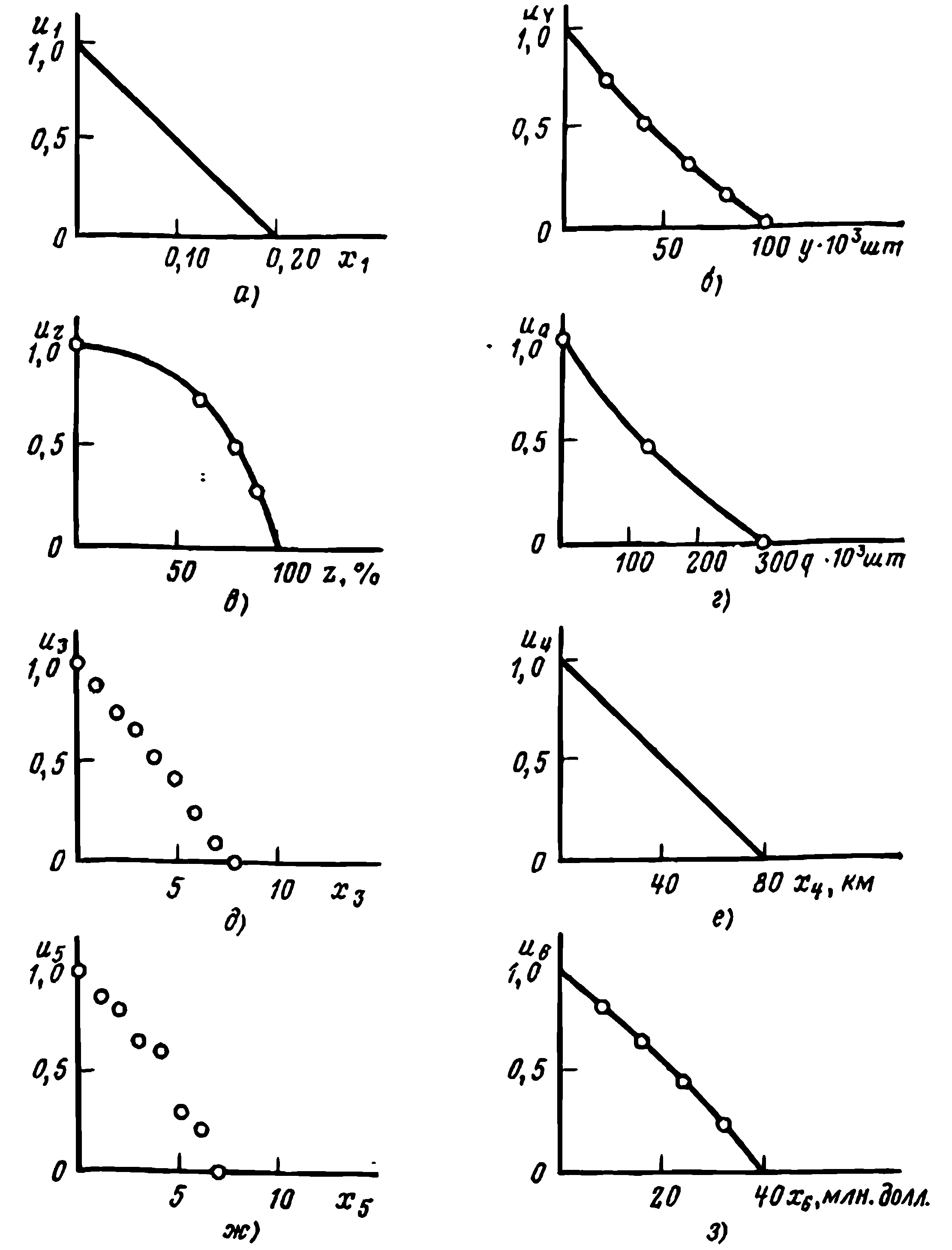
Рис. 3.1. Функции полезности для критериев компании WPPSS:
а — в координатах функции ценности v; б — d координатах критерия Z; 1 — исключенная иy(у)- 0,773; в—зависимость от процента потерь лососевых 2, uz-l,039X(z—100)]; г — зависимость от числа лососевых в р. Колумбия, q, UQ(q) (300—q); д — зависимость от уровня биологического воздействия 2а; е— зависимость от длины линии электропередачи Х4; u4(x4)=1—x4/80; ж — зависимость от уровня критерия социально-экономического воздействия хS; з — зависимость от ежегодных дифференциальных затрат для площадки
Приравнивание ожидаемых полезностей дает еще одну точку u (22) = 0,5 на графике функции полезности. Исходя из этого и была определена функция полезности в виде экспоненциальной кривой (рис. 3.1). В результате применения этой функции полезности для некоторых вспомогательных задач установлена ее приемлемость для оценки различных площадок.
Для искусственных шкал потребовалась модифицированная оценочная методика. Для того чтобы иметь хорошие оценки полезности для этих критериев, использованы только определенные точки на шкалах.
Например, при определении биологического воздействия из группы по выбору площадки спросили: «Пpи какой вероятности р биологическое воздействие, имеющее уровень 4 (см. табл. 3.3), эквивалентно лотерее с вероятностью р выигрыша соответствующего значению уровня 0, а значит, и выигрыша уровня 8 с вероятностью (1 — р)?». В результате рассмотрения нескольких значений р было установлено, что р = 0,6 является точкой (значением) равноценности. Затем было принято и3 (0) = 1 и и, (8) = 0, в таком случае и3 (4) = = 0,6. Аналогичные вопросы задавались до тех пор, пока значение функции полезности для каждого определяемого значения выбранной шкалы не было получено. Применялся ряд последовательных проверок, которые привели к некоторым изменениям в первоначальных оценках.
Нормированные функции полезности для каждого отдельного критерия приведены на рис. 3.1. Подробности оценок функций полезности и2 и и3 приводятся в [10]. Оценка u2 особенно интересна из-за наличия двух отдельных критериев, численности и процента потерь, которые требуется учитывать при описании возможных воздействий на лососевых. Поскольку критерий Х2 зависит от Y и Z (см. табл. 3.2), определим х2 = (у, z). Если в реке имеется менее 100 000 лососей, функцию полезности и2 можно представить в следующем виде:
![]()
где u — функции полезности, приведенные на рис. 3.1.
Дополнительно для рек, в которых более 300 000 лососей, была принята следующая функция полезности:
![]()
Для этого случая q = 0,01 yz. Функция полезности uq приведена на рис. 3.1. В исследованном нами районе нет рек с промежуточным значением численности лососей, т. е. от 100 000 до 300 000 шт., поэтому отсутствие непрерывности функции и2 для значений у между 100 и 300 тыс. было неважно.
Оценка весовых коэффициентов
Весовые коэффициенты оценивались в два этапа пятью членами проектной группы. Первый этап заключался в ранжировании критериев по их важности, второй — в определении значения. При ранжировании коэффициентов ki решался следующий вопрос. Если все шесть критериев находятся на низших уровнях (табл. 3.2), то какой из этих критериев наиболее желательно иметь на наилучшем уровне при условии, что остальные остаются на их наихудших уровнях? Ответ на этот вопрос соответствует критерию, для которого ki будет иметь наибольшее значение. Такая же процедура применялась и для других пяти критериев. Процесс повторялся до тех пор, пока не была закончена ранжировка всех коэффициентов ki.
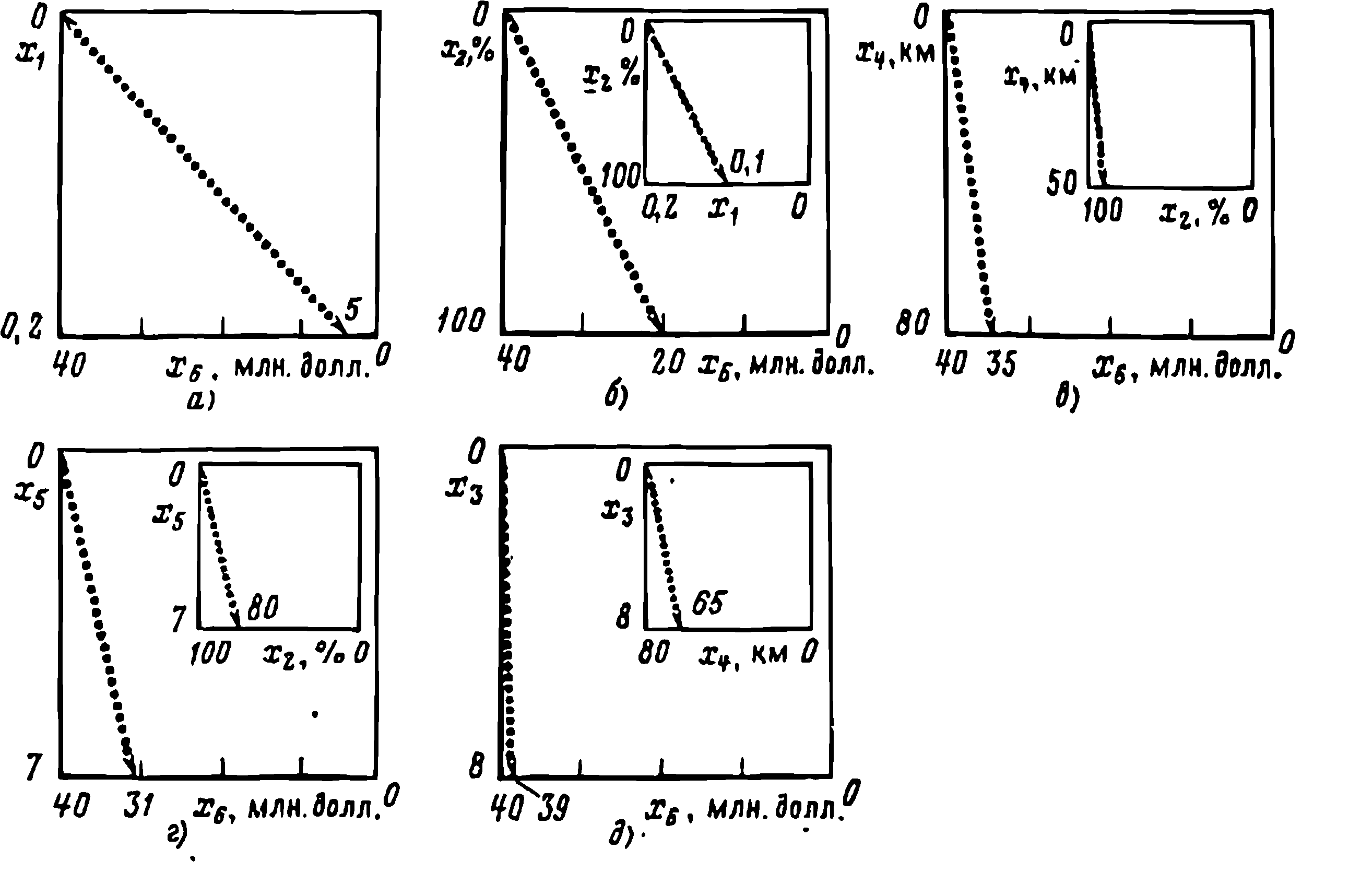
Ценностные соотношения, использованные при оценках весовых коэффициентов для компании WPPSS. (Пары точек равноценности указаны стрелками; ценностные соотношения, помещенные на графиках в рамку, используются для проверок): а — соотношение между фактором населенности x1 и ежегодными дифференциальными затратами х; б — соотношение между потерями лососевых в реке с численностью особей 100 000 шт. х2 и ежегодными дифференциальными затратами на площадку Х; в — соотношение между длиной линий электропередачи (в км) и ежегодными дифференциальными затратами (х6); г — соотношение между социально-экономическим воздействием и ежегодными дифференциальными затратами x6; д — соотношение между биологическим воздействием х3 и ежегодными дифференциальными затратами х6
Было установлено, что первым таким критерием является Хв — ежегодные дифференциальные затраты по площадке. Они изменяются от 40 до 0 млн. долл в год. Следует отметить, что если бы наибольшее (худшее) значение дифференциальных затрат по площадке было меньше 40 млн. долл., тогда могли бы передвинуться на первое место некоторые другие критерии. Из оставшихся пяти критериев населенность Χ1 является критерием, который больше остальных желательно переместить на наилучший уровень. Остальные критерии по порядку предпочтения в перемещении с худшего на лучшие уровни расположились в следующем порядке: Х2, Х5, Х4 и Х3. Рис. 3.2.
На следующем этапе определялись численные значения весовых коэффициентов. Это выполнялось путем установления ценностных соотношений между критериями. Эти ценностные соотношения определяют возможное изменение одного критерия за счет другого. Например, ценностное соотношение между критериями Х6 и Х1 было установлено исходя из следующих соображений:
при установлении соотношения k6 > k1 было найдено, что площадка А с ежегодными дифференциальными затратами на нее 0 долл, и значением населенности, равным 0,2, предпочтительнее площадки В с ежегодными дифференциальными затратами 40 млн. долл, и значением населенности 0. При этом все другие критерии для площадок А и В были зафиксированы на одинаковых уровнях. Следовательно, должна быть площадка С со значением населенности 0,20 и неопределенным значением ежегодных дифференциальных затрат между 0 и 40 млн. долл., равноценная площадке В. При этом все другие критерии для площадок В и С находятся на одинаковых уровнях.
Группа но выбору площадки пришла к выводу, что если бы для площадки С требовался уровень ежегодных дифференциальных затрат 5 млн. долл., то она была бы равноценна площадке В. Это значит, что группа по выбору площадки предпочла бы иметь увеличение ежегодных дифференциальных затрат на площадке с 5 до 40 млн. долл., но при этом переместить площадку из малонаселенного района (SPF=0,20) в ненаселенный район (SPF=0). Результат оценки этого ценностного соотношения представлен на рис. 3.2, а. Соотношения для остальных пар критериев приведены также на рис. 3.2. Из этих ценностных соотношений следует, что можно увеличить:
ежегодные дифференциальные затраты на площадку с 20 до 40 млн. долл, для сохранения всех лососевых в реке, в которой обитает 100 000 лососей;
ежегодные дифференциальные затраты на площадку с 35 до 40 млн. долл., чтобы новая линия электропередачи длиной 80 км не проходила через район с особо ценной природной средой;
ежегодные дифференциальные затраты на площадку с 31 до 40 млн. долл, для полного исключения нежелательных социально-экономических последствий резкого увеличения, а затем уменьшения численности рабочих в районе площадки (т. е. изменения значения уровня с 7 до 0 по искусственной шкале);
ежегодные дифференциальные затраты на площадку с 39 до 40 млн. долл, для полного исключения биологических воздействий на площадку (т. е. изменить значения уровня воздействия с 8 до 0 по шкале табл. 3.3).
Для проверки обоснованности ценностных соотношений эмпирическим путем были получены некоторые другие ценностные соотношения, не содержащие экономической категории затрат. Они показаны в рамках на рис. 3.2. Применение этих соотношений позволяет, например, допустить возможность потери всех лососевых в реке с численностью 100 000 особей, но при этом иметь возможность перенести площадку из слабонаселенной области (SPF = 0,2) в еще менее населенный район (SPF =0,1).
Последний этап в оценках весовых коэффициентов связан с определением вероятности р, при которой вариант I (с затратами на площадке, равными 0, и остальными критериями, находящимися на худших уровнях, см. табл. 3.2) и вариант II (описываемый лотереей, определяющей критерии на их лучших уровнях с вероятностью р или на худших уровнях с вероятностью 1 —р) равноценны. После рассмотрения ряда значений р группа по выбору площадки установила, что значения р сходятся на р = 0,4. С учетом всего вышесказанного остается только провести численные расчеты для определения весовых коэффициентов.
По определению, когда все критерии находятся на лучших уровнях, и — 1,0, а когда на худших, и = 0,0. Следовательно, ожидаемая Полезность лотереи для выбора вышеупомянутого варианта II равна
р(1,0)+ (1-р)(0, 0) = р = 0,4.
В соответствии с (3.3) значение полезности определенного последствия при выборе варианта I равно к0. Если два варианта выбора равноценны, то их ожидаемые полезности должны быть равны. В таком случае
![]() (3.5)
(3.5)
Определенные выше соотношения между затратами и другими критериями использовались для выражения всех других весовых коэффициентов через к6, поскольку к6 известно. Рассмотрим расчет весового коэффициента к1, связанного с критерием населенности Х1 в районе площадки. По определению точки равноценности для ценностных соотношений должны иметь равные ожидаемые полезности. Таким образом, исходя из точки равноценности для ценностного соотношения а, рис. 3.2, получаем
![]()
(3.6)
причем нет необходимости беспокоиться об установлении уровней других критериев, но, поскольку условия независимости предпочтений подтверждены ясно, то (3.6) действительно для всех значений критериев Х2, Х3, Х4 и Х5. В частности, предположим, что другие критерии находятся на их худших уровнях, таких, что и2 (х2) = u3 (x3) = u4 (х4) = u5 (х5) = 0. Тогда, используя (3.3) для (3.6), приравняем
![]()
Это выражение можно упростить
![]()
Зная из (3.5), что к6 = 0,40, получаем
![]()
Остальные весовые коэффициенты рассчитываются аналогично. В результате получаем

(3.7)
Константа к рассчитывается по (3.3) с использованием значений ki. Если (3.3) используется для определения наилучших значений всех критериев (т. е. все полезности равны 1,0), тогда к является решением уравнения
![]() (3.8)
(3.8)
Используя (3.7) и (3.8), получаем
к = —0,325. (3.9)
Многокритериальная функция полезности (3.3) полностью определится коэффициентами k1 из (3.7), к из (3.9) и однокритериальными функциями полезности, приведенными на рис. 3.1.

