ГЛАВА 3
МЕТОДЫ ПОИСКА ЭКСТРЕМУМА ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
Рассмотренные в предыдущей главе постановки задач о технико-экономической и массогабаритной оптимизации параметров теплообменных аппаратов сводятся к следующей математической формулировке.
Имеется нелинейная функция п переменных
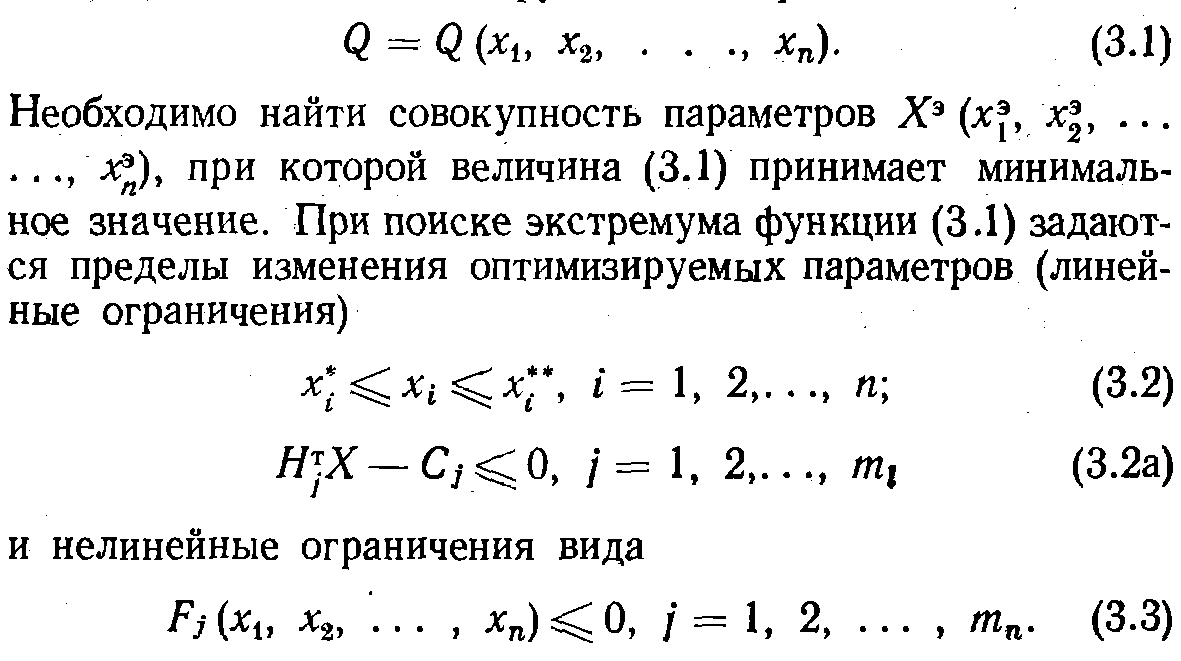
Ограничения (3.2), (3.2а) и (3.3) определяют допустимую область поиска. Если экстремум функции (3.1) находится внутри этой области, то он считается абсолютным экстремумом; если же его координаты находятся на границе допустимой области, то считается, что задача решена на условный экстремум.
Анализ зависимости критериев качества от изменения параметров оптимизации (см. рис. 1.5, 1.6, 2.1—2.12) показывает, что эти критерии являются, как правило, многоэкстремальными функциями и экстремумы могут быть как абсолютными, так и условными. Наличие многих локальных экстремумов предполагает поиск наилучшего из них — глобального.
Представленная задача относится к типу задач так называемой статической оптимизации. Рассмотрим существующие методы решения таких задач.
3.1. МЕТОДЫ ПОИСКА ЛОКАЛЬНЫХ ЭКСТРЕМУМОВ
Приводимый ниже обзор способов поиска экстремума функции многих переменных не претендует на полноту, а лишь преследует цель ознакомить специалистов других областей с наиболее популярными методами, имеющими практическое значение. Наиболее полно с практической точки зрения представлены методы в монографии [30] (включая программы рабочих алгоритмов), а также в [31]. Рассматривается задача нахождения минимума (3.1) при условиях (3.2), причем экстремальная точка лежит внутри области, выделяемой ограничениями (3.2).
Приводимые методы гарантируют сходимость к экстремуму, если функция (3.1) выпукла на области (3.2). В случае же существования в области (3.2) нескольких экстремумов при некоторых дополнительных условиях гарантируется сходимость к одному из экстремумов.
По характеру организации процесса поиска теоретические методы поиска подразделяются на две группы: детерминированные и случайные.
ДЕТЕРМИНИРОВАННЫЕ МЕТОДЫ ПОИСКА
Детерминированные методы поиска Характеризуются предварительным накоплением вспомогательной информации, на основе которой выбираются направление и длина рабочего шага. Как правило, эта информация носит локальный характер.
Одним из немногих приемлемых видов локальной информации о функции является ее вектор-градиент. Градиент указывает направление максимального прироста функции, дает некоторую информацию о расположении поверхностей равных значений функции в данной области и косвенно позволяет судить о близости к экстремуму. Естественно, что это столь эффективное понятие из классического анализа стало главным моментом в создании методов поиска. Первые методы непосредственно использовали градиент в выборе направления поиска, как, например, методы градиента и наискорейшего спуска [32—34], которые лежат в основе целой группы способов, разработанных в дальнейшем.
Методы параллельных касательных (ПК) [35]. Эта группа представляет различные модификации метода спуска, способствующие его ускорению. Все они построены на свойстве параллельности гиперплоскостей, касательных к поверхностям эллипсоидов в точках отрезка, проходящего через центр семейства концентрических эллипсоидов. Для такого случая эллиптических функций метод ПК позволяет определить точное положение оптимума после небольшого, заранее заданного числа шагов. Кроме того, он обладает свойствами, позволяющими двигаться по гребню и при неэллиптических линиях уровня.
Давно известен двумерный вариант УПК (ускоренный метод параллельных касательных). Нетрудно видеть, что зигзагообразная траектория поиска по методу наискорейшего спуска (подъема) целиком лежит в области, ограниченной двумя линиями, пересекающимися в вершине (рис. 3.1). Это наводит на мысль, что поиск надо вести вдоль прямой Р0Р3, в результате чего минимум будет найден после трех одномерных операций спуска. В случае трехмерного варианта УПК имеет место следующая последовательность: осуществляется двумерный вариант поиска, в результате чего на пятом шаге определяется плоскость, содержащая центр Xэ, и три точки на ней, затем в результате поиска на плоскости определяется Xэ.
При многомерном поиске имеет место следующая последовательность: применяя вариант поиска УПК на плоскости, определяем содержащую Xэ область Мη-1, затем и т. д., пока не придем к М1 — прямой, на которой определяем точку Xэ.

Схема поиска по ускоренному методу параллельных касательных
Сходным УПК является обобщенный метод параллельных касательных (ОПК), основанный на упомянутом выше свойстве касательных гиперплоскостей и заключающийся в следующем. В начальной точке Р0 проводится касательная гиперплоскость π0, и из нее в произвольном направлении осуществляется спуск в низшую точку (обозначение P1 с целью удобства нумерации опускается); здесь также определяется касательная гиперплоскость π. Затем из Р2 вновь совершается спуск параллельно гиперплоскости π0 (направление выбирается произвольно, но степеней свободы на одну меньше), в результате чего получится точка P4, в которой также находится касательная гиперплоскость π4; из P4 осуществляется подъем параллельно π0π2 в Р5, откуда совершается ускоренный спуск вдоль Р2Р5 в Р6 и т. д.

Схема поиска по обобщенному методу параллельных касательных
Таким образом, прослеживается следующая закономерность (рис. 3.2):
- в точках с четным индексом (k = 0, 1, ..., п—1, где п — число переменных) определяется касательная π2k;
- спуск из точек P2k осуществляется параллельно касательным гиперплоскостям π0, π2k. в результате чего получаем точки с нечетной нумерацией P2k+1;
- точки с четной нумерацией P2k определяются в результате ускоренного спуска вдоль линии Р2А-4Р2k-1 (k = 2, ...3 , ...n);
4) процесс заканчивается за 2n—1 одномерных шагов и измерений касательных плоскостей, включая Р2k.
Метод УПК имеет ту же закономерность, что и ОПК, с той лишь разницей, что спуск из точек Р2k осуществляется вдоль антиградиента. Кроме того, при этом автоматически осуществляется условие параллельности, так что УПК можно считать частным случаем ОПК.
В последнее время все чаще отказываются от процедуры спуска или подъема вдоль градиента и выбирают новое направление, имеющее свои преимущества.
Метод сопряженных градиентов [36—38] — один из самых популярных — нашел очень большое распространение. Рассмотрим его разновидности. Ищем минимум функции (3.1).
Алгоритм 1. Здесь, как и во всех модификациях, первый шаг делается в направлении антиградиента и вектор приращения имеет вид
3.1.
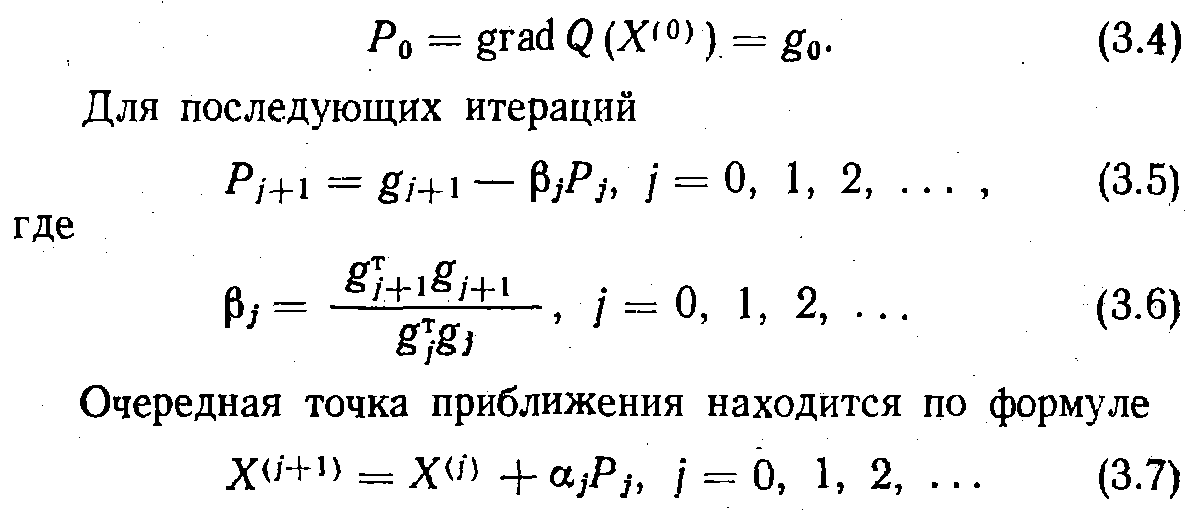
Здесь aj должно минимизировать функцию вдоль направления Pj.
Другой вариант поиска этим методом повторяет процедуру последовательно для и шагов по числу оптимизируемых параметров, после чего первое приближение из X(N) делается в направлении gn.
Алгоритм 2. Для данного алгоритма [38], по мнению авторов, характерна более высокая скорость сходимости для неквадратичных функций. Имеют место соотношения




a di равно сумме всех λi до того момента, как оси были повернуты в последний раз. В [46] предлагается новый подход к построению системы ортогональных векторов, который позволяет преодолеть ряд затруднений вычислительного характера.
Симплексный метод поиска [41, 47]. В некоторых случаях этот метод оказывается очень эффективным, так как рост числа оптимизируемых параметров не увеличивает потери на поиск.
Как известно, правильным η-мерным симплексом называют выпуклый η-мерный многогранник, у которого все вершины находятся на одинаковом расстоянии от центра, а длина всех ребер одинакова. В работе [47] было предложено использовать симплекс-планирование для поиска оптимального режима с несколькими параметрами. Суть поиска заключается в следующем: строим в пространстве параметров правильный симплекс, в одной из вершин которого находится начальная точка. Измеряем функцию в других вершинах симплекса. На каждой п—1-мерной грани симплекса можно построить другой правильный симплекс, имеющий п—1 общих вершин и являющийся зеркальным отображением первого. Доказано, что если движение совершается за грань симплекса, противоположную вершине с минимальным значением функции, то такое движение совпадает в пределе с движением вдоль градиента. Поэтому построение зеркального симплекса по отношению к минимальной вершине равноценно сдвигу в направлении, близком к градиентному.
МЕТОДЫ СЛУЧАЙНОГО ПОИСКА [48, 49]
Наряду с детерминированными методами поиска экстремума в последнее время обращают на себя внимание и завоевывают все большую популярность методы случайного поиска. Методы подкупают своей простотой, а также некоторыми открывающимися перспективами преодоления «проклятия размерности», присущего в значительной степени градиентным методам.
В, связи со спецификой систем оптимизации и выбранных нами оценок эффективности поиска мы в основном будем интересоваться шаговыми алгоритмами

Здесь и далее а — длина рабочего шага в пространстве параметров.
Поиск с пересчетом. Этот алгоритм является модернизацией предыдущего. Возвратный шаг при неудачной попытке в данном случае не производится, за счет чего алгоритм имеет повышенное быстродействие, возврат как бы пересчитывается вместе с последующим случайным шагом. Рекуррентная формула для смещения имеет вид
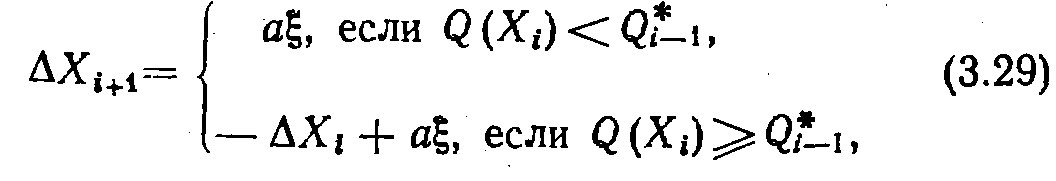


которая в пределе совпадает с направлением градиента функции качества. С другой стороны, среднее значение вектора по всем возможным реализациям пробных шагов также совпадает с направлением градиента. Таким образом, направление вектора при конечном т является статистической оценкой градиентного направления. Здесь направление рабочего шага
![]() (3.37)
(3.37)
Существенно то, что статистический градиент требует меньше замеров функции качества, чем его регулярный аналог.

