ГЛАВА 5. РЕЗУЛЬТАТЫ РАСЧЕТОВ ПО ПРОГРАММАМ ОПТИМИЗАЦИИ
Изложенные выше методы и алгоритмы были реализованы в виде программ оптимизации параметров теплообменных аппаратов для ЭВМ «Минск-32», «М-222», «БЭСМ-4». Программы были разработаны совместно сотрудниками Института систем управления АН Грузинской ССР и Института ядерной энергетики АН Белорусской ССР. Тексты некоторых из них на языке АЛГОЛ приведены в приложении.
Каждая из программ состояла из двух более или менее автономных частей: блока расчета критериев качества и функций ограничений и блока поиска оптимальных параметров. Такая структура позволяет в зависимости от конкретной практической задачи выбирать наиболее подходящий математический метод поиска (скалярный или векторный) локального, глобального или условного экстремума функции качества.
В частности, для обеспечения проектных разработок теплообменных аппаратов АЭС с диссоциирующим теплоносителем проводились расчеты по программам оптимизации противоточного регенератора-испарителя по критерию Ψρ (2.63а) с ограничением (2.26), конденсатора с водяным охлаждением со скалярными критериями качества Ψκ, Мк, Vк, Ψк, векторными и др. Ниже приводятся некоторые результаты расчетов по программам оптимизации.
5.2. ОПТИМАЛЬНЫЕ ПАРАМЕТРЫ КОНДЕНСАТОРА И СИСТЕМЫ ОХЛАЖДЕНИЯ
В настоящем параграфе представлены результаты расчетов оптимальных параметров конденсатора и системы охлаждения АЭС с реактором на быстрых нейтронах БРГД-1000, охлаждаемым диссоциирующим теплоносителем, электрической мощностью 1 млн. кВт БРГД-1000. Рассматривались разные варианты термодинамического цикла (высокотемпературный с максимальной температурой в цикле 840 К и низкотемпературный с температурой 620 К) с разными типами систем охлаждения (водохранилища и испарительные градирни). Оптимизация проводилась по различным критериям качества Фк (2.42), Мк (2.40), VK (2.41), Ψκ (1.3), ψ; (2.59) как скалярным, так и векторным методом. Кроме того, для сравнения проводилась отдельно минимизация стоимости системы охлаждения Фсо (2.60), зависящей от двух оптимизируемых параметров: кратности охлаждения х3 и начальной температуры охлаждающей воды х4. При поиске по критериям качества Фк, AfK, Кк и ψκ задавались ограничение по мощности на прокачку охлаждающей воды (2.43) (jV=CArmax= Ю МВт) и текущее ограничение (2.45). Кроме этих нелинейных ограничений, во всех вариантах разрешенная область изменения оптимизируемых параметров задавалась следующим образом (линейные ограничения): 8 мм≤х1≤30 мм с шагом 1 мм; 0,5≤х3≤3,0 м/с с шагом 0,1 м/с; 5≤х3≤40 с шагом 1; 286 K≤x4≤294 К с шагом 0,5 К.
В табл. 5.2 приведены результаты расчета оптимальных параметров для низкотемпературного варианта схемы АЭС, в табл. 5.3 — для высокотемпературного. В скобках приведены значения неминимизируемых в данном варианте критериев качества.
Таблица 5.2
Результаты расчетов по программам оптимизации для конденсатора низкотемпературного варианта разработок АЭС БРГД-1000 (система охлаждения — пруды-охладители, климатические условия—центр европейской части СССР).

Нижняя граница допустимых значений.
Верхняя граница допустимых значений.
Таблица 5.3
Результаты расчета локальных экстремумов при оптимизации параметров конденсатора высокотемпературного варианта разработок АЭС БРГД-1000

Параметр находится на нижней границе допустимых значений.
** Параметр находится на верхней границе допустимых значений.
Скалярная оптимизация.
Оптимизация параметров конденсатора с целью достижения минимальной массы Vκ или минимального объема Vк дает один и тот же тривиальный результат: максимально допустимые скорости воды и кратности охлаждения и минимально допустимые диаметры трубок и начальные температуры охлаждающей воды. Однако этот вариант не является самым экономичным: стоимость конденсатора Фк при этом почти в 1,4 раза, а стоимость системы охлаждения Фco в 3,4 раза превышают соответствующие минимально возможные стоимости.
Поиск оптимальных параметров по критерию минимальной стоимости конденсатора (вариант 2 в табл. 5.2) приводит не только к существенному ее уменьшению (на 2,8 млн. руб.), но и к снижению стоимости системы охлаждения. Достигается это за счет значительного увеличения диаметра трубок и уменьшения кратности охлаждения и небольшого снижения скорости воды в трубах. Увеличение диаметра связано с уменьшением удельной стоимости труб, а уменьшение кратности и скорости воды обусловлено ограничением мощности на прокачку (2.43).
Критерии Фк (Кк, Л1к) и Ф00 взаимно противоречивы по отношению к параметрам оптимизации х3 и х± Характерно, что в рассматриваемом случае минимально возможные стоимости конденсатора и системы охлаждения примерно равны.
Применение комплексных скалярных критериев Ψκ (1.3) и (2.59) в процессе оптимизации приводит к наилучшим показателям для комплекса конденсатор — система охлаждения (варианты 5 и 6 в табл. 5.2). В этих случаях как стоимость конденсатора, так и стоимость системы охлаждения находятся достаточно близко к своим минимально возможным значениям. Интересно отметить, что расчеты по программе оптимизации с критерием качества (стоимость установленного киловатта) дают лучшие результаты по сравнению с расчетами по программе с критерием качества Ψκ (стоимость комплекса конденсатор — система охлаждения) не только по показателю Ψ'κ, но и по Ψκ. Остановимся на этом несколько подробней.
В табл. 5.3 приведены значения как глобальных, так и нескольких локальных экстремумов функций Ψκ и для высокотемпературного варианта АЭС БРГД-1000 с различными системами охлаждения. Характерно, что почти во всех вариантах оптимизация по критерию Ψκ. дает несколько лучшие абсолютные результаты, чем по критерию Ψκ, хотя оптимальные параметры, например, в точках глобальных экстремумов не слишком сильно различаются между собой. Это объясняется тем, что в программе оптимизации с критерием Ψ κ отсутствует нелинейное ограничение мощности на прокачку охлаждающей воды (2.43), а экстремумы функции ψκ являются, как правило, условными, так как находятся на этой нелинейной границе. Таким образом, расчеты по программе с критерием Ψ' κ дают еще и дополнительный результат — оптимальное значение мощности на прокачку охлаждающей воды. Как следует из табл. 5.3, при использовании градирен экономически целесообразно увеличивать затраты мощности на прокачку воды в 1,5—2 раза по сравнению с водохранилищами-охладителями.
Отметим, что с точки зрения затрат машинного времени более «выгодной» является программа с критерием Ψκ, поскольку организация поиска по ней, основанная на быстром приближении к нелинейной границе, требует для достижения точки локального экстремума в среднем в 1,5 раза меньше элементарных шагов, чем по программе с критерием без нелинейного ограничения (2.43).
Векторная оптимизация.
Применяя метод векторной оптимизации к задаче поиска оптимальных параметров конденсатора и системы охлаждения, авторы ставили перед собой две цели: получить новую, заранее трудно предсказуемую информацию о возможных компромиссных решениях, удовлетворяющих одновременно нескольким противоречивым критериям качества, а также проверить эффективность самого метода и некоторых его модификаций в условиях данной задачи. В соответствии с подходом, изложенным в гл. 4, задача векторной оптимизации сводится к минимизации в области допустимых значений Ω параметров х1, х2, ..., хп выражения


Результаты расчетов по программе векторной оптимизации с различными критериями качества представлены в табл. 5.2 (варианты 7—9). Оптимизация по двум критериям Mк и Фсо, противоречивым в отношении параметров х3 и х4, дает компромиссное решение, в котором достигается и сравнительно небольшая масса конденсатора, и близкая к .минимально возможной стоимость системы охлаждения. Отметим, что этот вариант отличается от варианта оптимизации по скалярному критерию Ψκ меньшими значениями диаметра труб x1, скорости воды х2, кратности охлаждения х3 и несколько большим значением температуры охлаждающей воды х4.
Таблица 5.4
Изменение оптимальных параметров в зависимости от показателя Р в формуле (5.2)

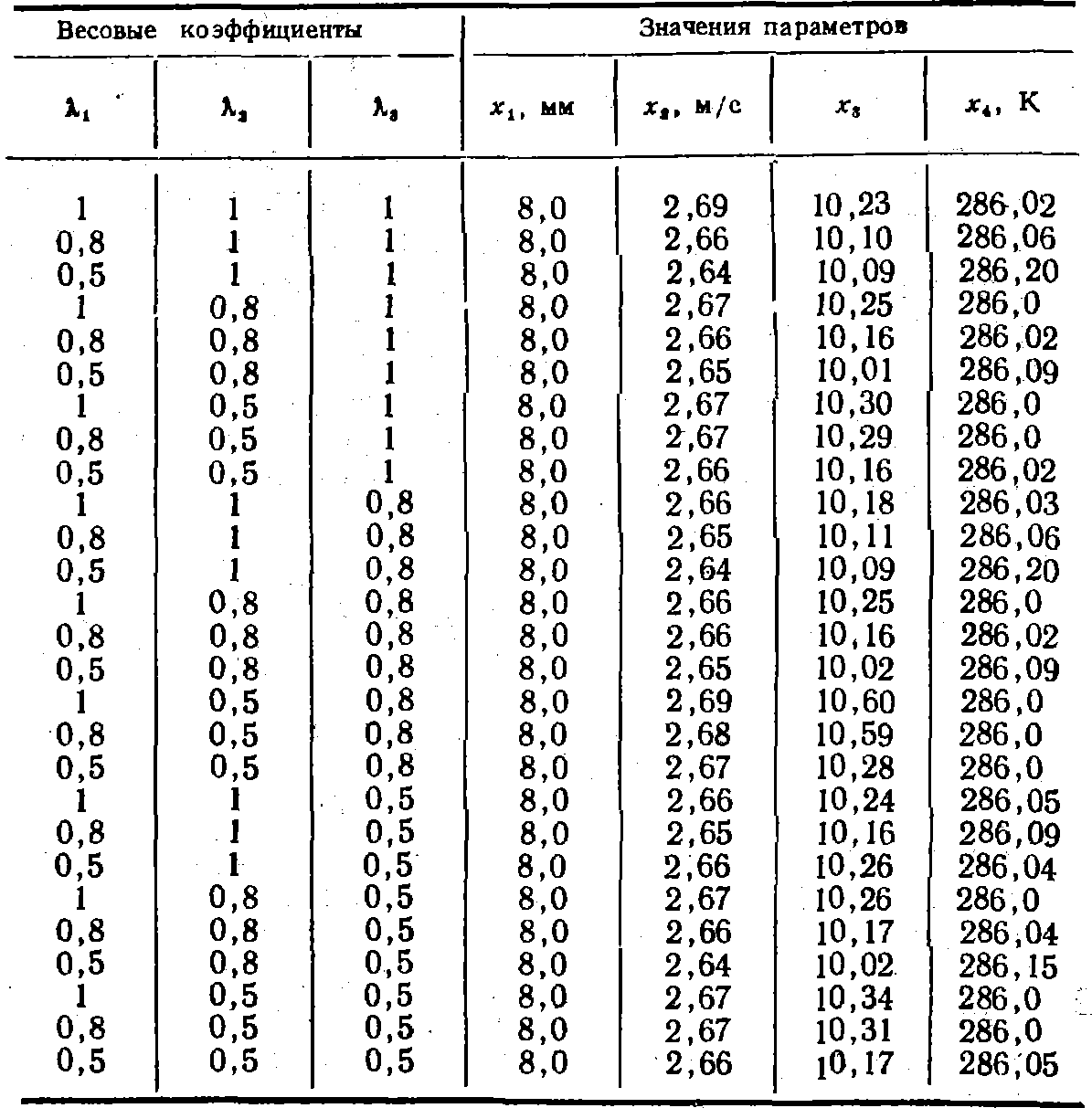
Т а б л и ц а 5.5
Изменение значений параметров оптимизации в зависимости от весовых коэффициентов λ3 в формуле (5.3)
В настоящее время весьма перспективной по соображениям безопасности является идея так называемой интегральной компоновки АЭС с размещением всего оборудования под единым бетонным колпаком. В этом случае одним из важнейших показателей качества, помимо стоимости, является объем, занимаемый оборудованием. В табл. 5.2 (вариант 8) приведен результат оптимизации по векторному критерию {Vк, Ψк}, который дает удовлетворительное решение: близкий к минимально возможному объем конденсатора и малую стоимость комплекса конденсатор — система охлаждения. В таблице приведен также вариант оптимизации параметров конденсатора и системы охлаждения по трем критериям качества Vк, Мк и Фсо. Здесь по сравнению с вариантом оптимизации по вектору {Мк, Фсо} усиливается «влияние» минимальной массы (минимального объема) и параметры х2 и х4 приближаются к оптимальным по скалярному критерию качества Мк (или Vк).
Следует отметить, что введение квадрата евклидовой нормы (5.1) как меры приближения к идеальной точке— не единственное решение проблемы. Более общим видом функции приближения является норма

при различных значениях весовых коэффициентов λ. Изменение λ от 0,5 до 1 мало влияет на значения оптимальных параметров. Таким образом, применение наиболее простой евклидовой метрики в качестве меры приближения к идеальной точке в задачах векторной оптимизации теплообменных аппаратов наиболее рационально.

