Изложим новую постановку задачи линейного (нелинейного) программирования по векторному критерию, в основу которой положена та же идея приближения, что и в параграфе 4.2.
Пусть задана система линейных форм
4.3.


4.3.


Усложнение данной задачи состоит в представлении функций g0(X), g1(X), gn(X) в виде комбинации позиномов (4.16). Решение поставленной задачи, естественно, можно осуществить общими методами нелинейного программирования. Широкое распространение получили методы нелинейного программирования применительно к задачам данного типа, рассматривающим целевую функцию и ограничения в виде позиномов (4.16). Эти методы получили название методов геометрического программирования.
Определение параметров проектируемой системы из условия минимизации лишь функции g0(X) во многих случаях неприемлемо, поскольку при этом не принимаются во внимание другие, не менее важные показатели качества системы. Для эффективного решения проблемы следует прибегнуть к представлению задачи инженерного проектирования как задачи векторной оптимизации: определить
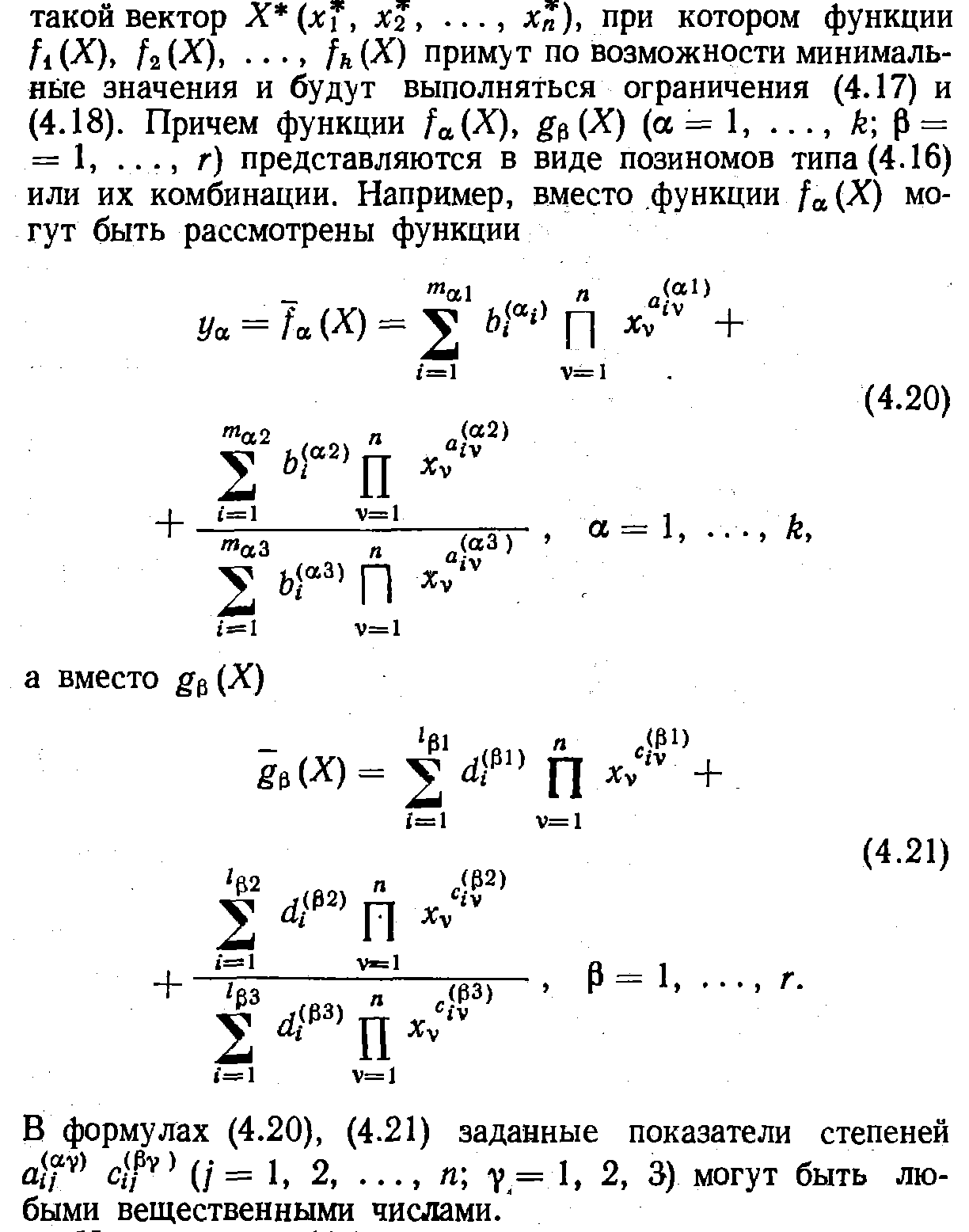
Неравенства (4.18) в пространстве переменных x1, х2, ..., хп определяют допустимую область Ω изменения параметров системы. Наиболее вероятно, что область Ω не окажется выпуклой. Для решения поставленной задачи векторной оптимизации имеет смысл применить метод приближения функций (4.20) к своим идеальным значениям в пространстве критериев качества системы.


