Метод предполагает аппроксимацию поверхности минимизируемой функции в уже найденных точках гиперплоскостями, касательными поверхностям в
Когда число базисных точек равно n+1, очередное приближение получаем однозначно решением системы (3.64), при меньшем числе базисных точек приходится делать выбор на определенном подмножестве.
Такая организация поиска выгодно отличает метод от многих градиентных методов тем, что она учитывает предыдущую информацию непосредственно в области поиска. Это позволяет учитывать изменение условий и эффективно выбирать направление шага, например, в узком овраге.
ИТЕРАТИВНАЯ ПРОЦЕДУРА МЕТОДА
Как было сказано выше, очередное приближение к экстремуму в методе касательных плоскостей выбираем на некотором подмножестве пересечений гиперплоскостей, касательных точкам, полученным на предыдущих итерациях. Рассмотрим более подробно принцип выбора и приведем алгоритм выбора.
Допустим, что имеется k базисных точек и соответствующие им системы (3.64) и (3.65). Базисные точки 
в ходе поиска всегда выбираются таким образом, что они удовлетворяют неравенству (3.65).
Ставится задача определения вектора, принадлежащего проекции множества пересечений гиперплоскостей на Еп, и осуществления рабочего шага вдоль этого направления.
Представим (3.64) в виде
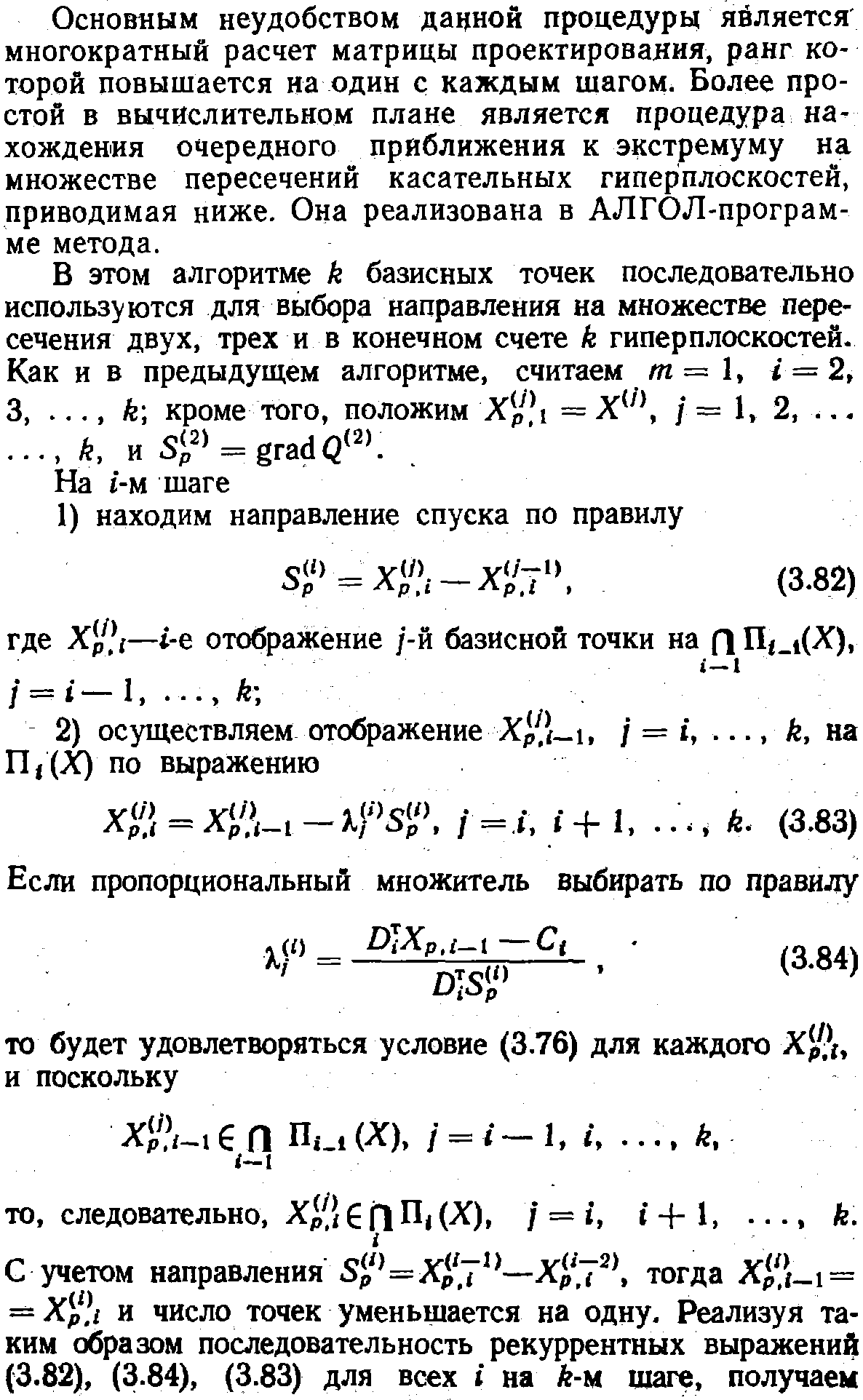
3.3.
, принадлежащие множеству пересечения k гиперплоскостей.
Описанная выше последовательность в вычислительном плане значительно лучше. Здесь необходимо L раз реализовать выражения (3.83), (3.84), где
(3.85)
и k раз — выражение (3.82), в то время как обращение матриц и операции над ними, производимые в первом алгоритме, требуют несравненно большей вычислительной работы. Правда, конечные итоги при
у этих двух алгоритмов различны, но в результате они со статистической точки зрения приводят к одинаковым результатам.
Если
уже является очередным приближением, в противном случае очередное приближение ищется по формуле (3.81). Здесь можно использовать любую стратегию одномерного поиска. Чаще всего принято отыскивать в «овраге» точку, в которой на данном направлении функция перестает убывать, так как переход за «гребень» дает в общем случае худшую точку, что в конечном счете влияет на сходимость. Характер поиска методом касательных плоскостей таков, что на последующих шагах происходит по существу самокорректировка и этот неудачный шаг мало влияет на качество поиска в целом.
ОГРАНИЧЕНИЯ
При наличии в задаче оптимизации ограничений в практической реализации метода всегда может возникнуть ситуация, когда очередное приближение попадает в запретную область или на ее границу. В этом случае к алгоритму предъявляется требование осуществлять спуск таким образом, чтобы в конечном счете не нарушались ограничения, накладываемые на переменные самой задачей.
Допустим, на переменные наложено т ограничений:
где (3.86), (3.87) — соответственно системы линейных и нелинейных неравенств, причем m=mi+mn. Необходимо сказать, что двусторонние ограничения, накладываемые на каждую переменную, представлены в виде пар обычных линейных неравенств и введены в (3.86).
Общая идея выработки поведения при нарушении очередным приближением одного или нескольких ограничений заключается в следующем: к системе (3.64) последовательно добавляются линейные или линеаризованные (в случае нелинейного неравенства) уравнения, соответствующие тем ограничениям, которые нарушены.
Последовательно реализуем алгоритм нахождения приближения на подмножестве пересечений до тех пор, пока не получим точку на границе допустимой области. Когда точка находится на границе, встает вопрос организации поиска вдоль границы, в случае если она существенна в этой точке т. е. скалярное произведение градиентов функции качества и функции ограничений отрицательно (случай минимизации). Таких границ может быть несколько. В общем случае имеем следующую систему:
Поиск вдоль границы.
Точка, лежащая в допустимой области, принимается за «базисную». В ней измеряются значение функции, градиент и строится новое «текущее» ограничение, на котором проверяются остальные «базисные» точки и строится новая система (3.64). Дополнительно в (3.64) вносятся уравнения, соответствующие тем существенным линейным границам, на которых лежит новая «базисная» точка.
Реализуется алгоритм нахождения очередного приближения и вновь полученная точка проверяется на ограничениях согласно пунктам 1 и 2, описанным выше, и в конечном счете находим еще одно приближение к экстремуму.
МОДИФИКАЦИЯ МЕТОДА
Метод касательных плоскостей базируется на использовании определенной рабочей информации о функции, получаемой на предыдущих приближениях. Поверхность функции аппроксимируется линейной многогранной поверхностью, на грани которой делается рабочий шаг. В случае сложной функции при таком поиске последовательность приближений не всегда получается монотонно убывающей, что в известной степени отрицательно влияет на поиск.
Задачей модификации метода является улучшение процесса поиска при том же объеме рабочей информации за шаг. Это достигается введением дополнительного критерия близости к экстремальной точке Xэ, учитывающего некоторые дополнительные качественные признаки, ха: рактеризующие положение той или иной «базисной» точки.
Модификация алгоритма предполагает на каждом рабочем шаге поиска вводить в систему (3.64) корректирующие множители
(3.96)
В уравнение для каждой гиперплоскости вводится множитель к составляющим вектора градиента, в связи с чем фактически изменяется угол наклона гиперплоскости к пространству оптимизируемых параметров X∩Еn·
Коррекция должна быть такой, чтобы множество пересечения базисных гиперплоскостей было ближе к «гребню» и соответственно к Хэ. При такой коррекции одна гиперплоскость берется опорной, и соответствующий ей коэффициент коррекции равен единице. Расчет других коэффициентов ведется относительно этой гиперплоскости. За опорную целесообразно принимать гиперплоскость, соответствующую максимальной базисной точке, для которой выполняется условие
Расчет по (3.98) и (3.99), естественно, невозможен, однако на основе ряда соображений практического характера можно составить приближенное выражение, для
вычисления которого достаточно рабочей информации поиска.
Анализируя первое слагаемое (3.98), можно утверждать, что отношение длин проекций векторов 
и 
на градиенты в точках .
пропорционально отношению модулей этих градиентов. Поэтому слагаемое пропорционально отношению квадратов модулей этих градиентов. Данная зависимость устойчива для линий равных значений функции «овражного» типа. Для второго слагаемого трудно найти объективный аналог, поэтому выражение (3.98) приближенно можно рассчитывать по формуле
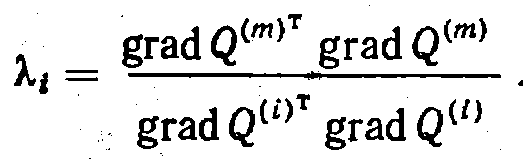(3.100)
Практика показала, что для линий равных значений функции, близких к эллипсоидам, лучше подходит несколько другой аналог [57]. Эксперименты на ЭВМ свидетельствует о том, что модификация повышает качество поиска в 1,5—2 раза.
СХОДИМОСТЬ МЕТОДА
Рассмотрим сходимость метода касательных плоскостей на выпуклой функции. При такой организации поиска, когда рабочий шаг очень мал, получаем последовательность точек, монотонно приближающуюся к Хэ без выхода за «гребень». В такой постановке новое приближение отбрасывает предыдущую базисную точку, и фактически имеем метод градиента, сходимость которого при достаточно малых шагах теоретически доказана [34]. При больших рабочих шагах в методе касательных плоскостей (в отличие от градиентного) система «текущих неравенств»(3.65) не расходится и в конечном счете образует на
, замкнутую выпуклую область, внутри которой находится Xэ. Итеративный процесс представляется как стягивание п+1 «базисных» точек вокруг Xэ. Если показать, что «базисные» точки лежат бесконечно близко друг к другу и одновременно
, то с определенного момента эти точки можно считать лежащими
откуда
(3.119)
а значит, имеет место выражение (3.101).
